加筋土挡墙稳定性分析的点安全系数法

杨果林，刘泽

(中南大学 土木工程学院，湖南 长沙，410075)

加筋土挡墙主要是将高模量的土工合成材料成层铺设在土体内，通过筋土间的摩擦耦合作用，提高土体自身的承载能力而发挥支挡作用。加筋土挡墙不仅具有优良的地基适应性和结构抗震性，而且施工简便，工程造价低，在公路、铁路、水利、市政工程等领域得到广泛应用[1]。由于筋材的加入，加筋土挡墙内部的应力和应变要比重力式挡墙或素土边坡的应力和应变复杂得多。国内外研究者对加筋土挡墙的稳定性分析方法进行了研究，提出了多种分析方法，如极限平衡法、能量法、位移法、K刚度法、滑移场法、数值计算法等[1-5]。目前,我国的各种规范如《公路路基设计规范》(JTGD 30—2004)、《铁路路基设计规范》(TB 10001—2005)等还是采用极限平衡法进行分析，并将加筋土挡墙的稳定性分为内部稳定性和外部稳定性 2部分。内部稳定性主要校核筋材的抗拉和抗拔稳定性；外部稳定性主要校核挡墙抗倾覆、抗滑动和整体稳定性。极限平衡法没有考虑加筋土挡墙各组成部分内部的应力和应变关系及其相互作用，而且需要对滑裂面的形状进行假设，如假定为折线形、圆弧形或对数螺旋线形等[5]。随着计算机技术的发展，数值分析方法已成为加筋土结构分析的有效方法，并发展有多种计算模式，如筋土分开模拟法、复合材料法、等效附加应力法等。数值分析法不但满足力的平衡条件，而且考虑了材料的应力应变关系以及填料与筋材间的相互作用。刘华北等[6-7]采用数值方法研究了加筋土挡墙的稳定性及其影响因素。近年来，基于数值分析的强度折减法(Shear strength reduction, SSR)在岩土工程稳定性分析中得到推广，其基本思想是[8-10]：通过1个逐渐增大的折减系数ω不断减小岩土体的抗剪强度参数(c和φ)。当工程结构达到临界状态发生破坏时，对应的折减系数即为安全系数。基本公式为：

式中：c为黏聚力；φ为内摩擦角；c′为折减后的黏聚力；φ′为折减后的摩擦角；ω为折减系数。

王清等[11-12]将强度折减法引入到加筋土挡墙的稳定性分析中，不仅得得挡墙的安全系数，而且得到挡墙失稳时滑裂面的位置与形状，计算结果非常直观。在此，本文作者提出用点安全系数法分析加筋土结构的稳定性。在理论分析基础上，推导岩土体、筋材、筋土界面的点安全系数和筋材抗拉与抗拔安全系数的计算方法，给出点安全系数法在 FLAC3D软件中的实现步骤与 FISH命令，并通过工程实例分析，对比点安全系数法与强度折减法的差异。

1 点安全系数的定义

广义上，材料受到荷载作用时，若其应力应变状态满足一定条件，则材料就可能发生屈服或破坏现象，这称为屈服条件，一般可表示为：

式中：f为某函数关系；σ为总应力；材料参数H为内变量κ的函数。

为了表征受荷材料的安全状态，工程上可以将安全系数定义为材料在一定条件下的屈服强度与其实际应力状态之比[13]，即

当Fp＞1时，材料的实际应力状态位于屈服面内，材料未破坏；当Fp=1时，材料的实际应力状态位于屈服面上，材料处于临界状态；当Fp＜1时，材料受到的应力超过其强度极限，材料已破坏。

在数值分析时，通常将分析对象离散为一个个单元体，在获得各个单元体的应力状态后通过式(3)即可获得每个单元体的安全系数即点安全系数。点安全系数法在边坡、隧道等工程领域内已得到应用，结果表明：这种方法非常适合分析复杂应力状态下工程结构不同部位的稳定性[13-15]。

1.1 岩土体的点安全系数

加筋体及其后的填料、地基、临近边坡等主要是由岩土类材料所构成。当采用Mohr-Coulomb准则作为岩土材料的屈服准则时，材料的破坏取决于剪应力和正应力的联合作用(压为正，拉为负)，其屈服函数可表示为：

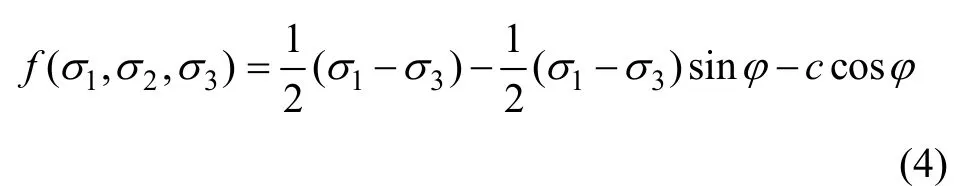
式中：σ1，σ2和σ3均为主应力；c为黏聚力；φ为内摩擦角。

由式(3)可以得到基于Mohr-Coulomb准则的岩土体点安全系数表达式：

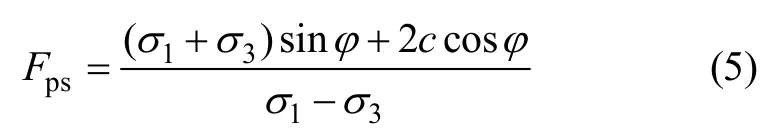
1.2 筋材的点安全系数

加筋土工程中筋材(带)通常是由金属或高分子聚合物(聚乙烯、聚丙烯等)加工而成。与岩土材料相比，筋材一般可视为线弹性体，并且只能受拉不能受压。根据弹性理论，拉应力作用下筋材单元的安全状态可以用下式表示：

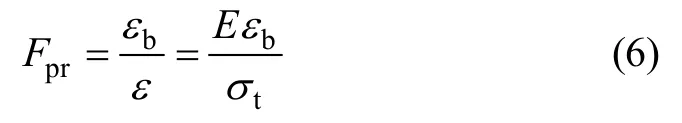
式中：εb为筋材断裂时的极限应变；ε为筋材的拉应变；E为筋材的弹性模量；σt为筋材单元受到的拉应力。

对于加筋体内第i层筋材，点安全系数最小的单元是最危险的单元，其点安全系数也就是该层筋材的抗拉安全系数。筋材在施工时会受到一定的机械损伤，以高分聚合物为原料的土工合成材料在使用过程中可能出现老化、蠕变现象。在工程中，通常需要对筋材的强度进行折减以作为筋材的长期强度，有时还需要控制挡墙的侧向变形率。因此，式中的筋材极限应变可以采用允许应变[ε]表示。

1.3 筋土界面的点安全系数

筋土界面关系是加筋土结构研究的核心内容之一。进行数值分析时，若采用筋土分开模拟方式，则通常需设置界面单元以反映填料与筋材之间的摩擦耦合关系。筋材抗拔稳定性验算就是对筋土界面不发生整体屈服的稳定性进行验算。

设筋土界面关系符合Mohr-Coulomb屈服准则：

式中：τf为界面极限剪切强度；σn为法向压力；φif为筋土界面摩擦角；cif为筋土界面黏聚力。

筋土界面单元的点安全系数Fif可表示为：

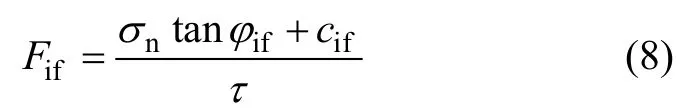
式中：τ为筋土界面间的剪应力。

由式(8)可以获得筋土界面单元在受到拉应力作用时不发屈服的点安全系数，但不是筋材的抗拔安全系数。加筋土挡墙分析时通常将加筋区分为活动区和锚固区2部分，只有位于锚固区的筋材长度才提供抗拔阻力。活动区和锚固区的分界点为各层筋带最大拉应力点的连线[5]。考虑到锚固区内各界面单元对抗拔稳定性的贡献，第i层筋材的抗拔安全系数可定义为：

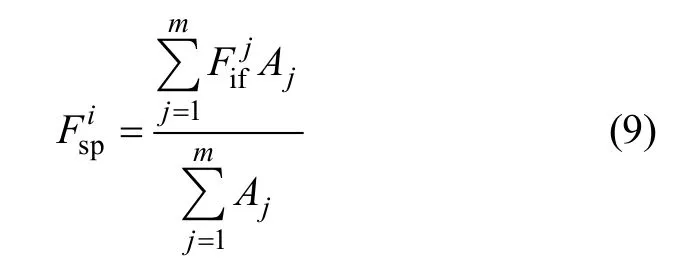
式中：Aj为位于第i层筋材锚固区内的筋材单元面积；m为第i层筋材锚固区内筋材单元的个数。

2 点安全系数法在FLAC3D中的实现方法

FLAC3D软件是目前岩土工程中应用比较广泛的数值分析软件，不仅提供了多种本构模型和结构单元，而且提供了功能强大的 FISH语言，并为单元体、节点、结构单元和结点都提供了相应的额外变量可以为加筋土挡墙分析模型中的岩土体单元、结构单元和结点单元赋予新的属性值[16]。

在 FLAC3D中计算加筋土挡墙稳定性的点安全系数的步骤如下。

(1) 根据工程实际建立数值分析模型，并运行模型平衡。

(2) 利用 FLAC3D软件的单元遍历语言给每个单元体、节结单元和结点分配1个额外变量。

(3) 按照式(5)，(6)和(8)分别计算单元体、节结单元和结点的点安全系数。

(4) 将步骤(3)所得计算结果分别存放到步骤(2)所建立的相应额外变量中；

(5) 利用Plot命令或Tecplot软件对计算结果进行后处理，得到挡墙岩土体单元、筋材单元和界面单元的点安全数分布云图或等值线图。

以岩土体的点安全系数计算为例，其实现过程如下：

new

res reinforedwall.sav ；读取加筋土挡墙数值计算结果

config zextra 1

def Fs_point

p_z=zone_head

loop while p_z # null

a=z_sig1(p_z)+z_sig3(p_z)

b=z_sig1(p_z)-z_sig3(p_z)

fric=z_prop(p_z,′friction′)

cohesion=z_prop(p_z,′cohesion′)

Ks=((a-b*sin(fric))*tan(fric)+2*cohesion)/(b*cos(fric))

z_extra(p_z,1)=Ks

p_z=z_next(p_z)

end_loop

end

Fs_point

plot con zextra 1

3 实例分析

3.1 分析模型

绍诸(浙江绍兴—诸暨)高速公路 K38＋325～K38＋485段位于经济发达的诸暨市枫桥镇内，右侧紧临交通繁忙的绍大线。为了提高路基的稳定性、减少耕地占用和节约工程造价，营造优美的公路景观，这一路段采用绿色加筋格宾挡土墙，墙高10.62 m，共布设有12层双绞合六边形网丝网筋材，层高0.76 m，墙面倾角为65°。

根据 K38＋398断面的施工设计图可建立如图 1所示的半路堤式分析模型，模型顶宽13.00 m。为了消除边界影响，以墙趾为原点，向前和向下各取10 m，模型总高20.62 m，长20.00 m，宽1.00 m。路基填料及地基土体采用Mohr-Coulomb，筋材采用FLAC3D软件自带 geogrid单元模拟。这种单元通过弹簧—滑块系统考虑了筋材与填料间的界面关系，并符合Mohr-Coulomb屈服准则。

图1 加筋土挡墙分析模型Fig.1 Analysis model of reinforced earth retaining wall

3.2 计算参数

根据工程地质勘察资料和室内试验，确定计算参数如表1和表2所示。

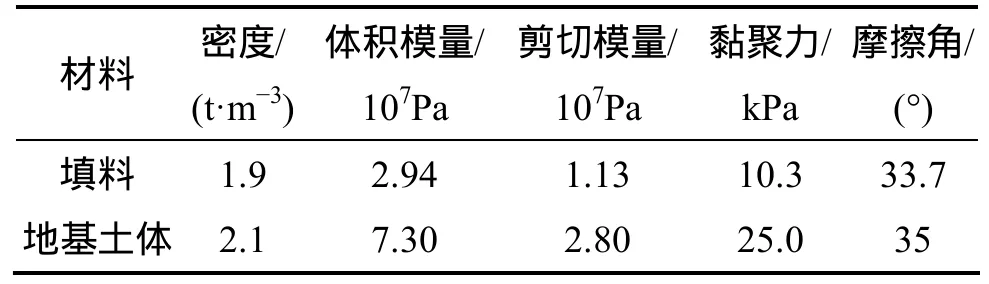
表1 岩土体的力学参数Table 1 Mechanical parameters of soil and rock

表2 筋材及筋土界面的力学参数Table 2 Mechanical parameters of reinforcement and interface

3.3 结果分析

分析时先对地基进行计算，待平衡后再填筑路堤。由于实体工程的施工速度很快，模拟时认为路堤是一次性填筑完成。路基填筑完成后再在模型顶部施加10 kN/m的等效车辆荷载。

工程施工时，分别在K38＋353和K38＋398这2个断面埋设土压力盒、柔性位移计和土应变计等元器件，对挡墙的稳定性进行监测。为了验证模型的正确性，这里取部分数值进行分析。图2所示为K38＋398断面的墙面侧向位移模拟值与实测值的对比结果。从图2可以看到：两者在挡墙侧向变形分布模式上完全相同，数量上的差别也不是很大(＜4 mm)。这一差别主要是模拟时考虑了作用在墙顶的车辆荷载所致。因而，所建立的数值分析模型能够反映实体工程的实际状况。

图2 38＋398的挡墙的侧向变形Fig.2 Lateral deformation of retaining wall for K38＋398

首先采用FLAC3D自带的强度折减法(solve fos 模块)计算挡墙的安全系数。图3所示是折减系数为1.93时挡墙内的剪应变增量云图。由图3可知：强度折减法的优点在于与传统稳定性分析观念相符合，不仅给出了挡墙的安全系数(1.93)，而且将潜在滑动面的位置及形状都直观地表现出来；该加筋土挡墙的潜在滑动面位置较深，基本上都在加筋体之外，相当于规范要求的进行整体稳定性计算，没能反映加筋体的安全状态，更没能表达筋材的安全性。图4所示为挡墙内点安全系数分布等值图。从图4可以看到：点安全系数法将加筋体、墙后填土以及地基等各个位置的安全状态定量的表示出来，也很直观。与图3相比较，挡墙内安全系数最小的位置并不是在由强度折减法得到的滑动带处，而是在靠近面墙的中下部加筋体内，其安全系数为1.5左右，这一位置也正是挡墙产生侧向变形最大的位置(见图2)。

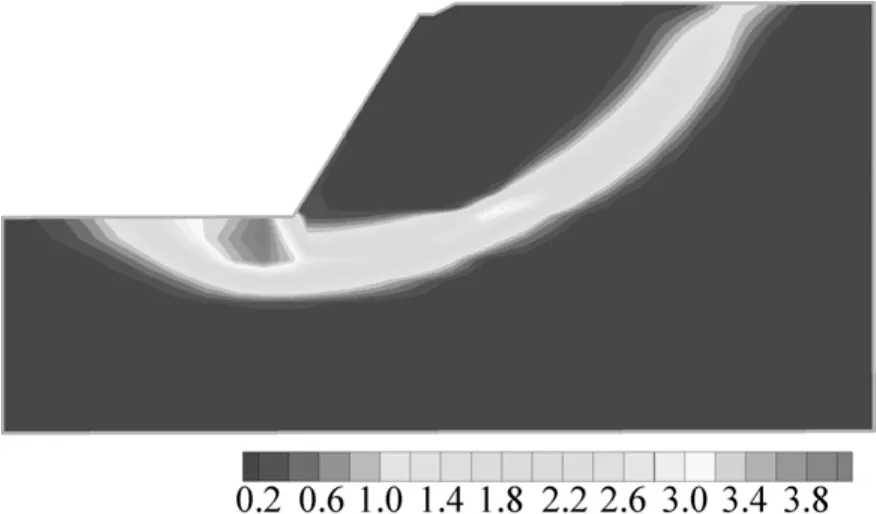
图3 采用强度折减法所得挡墙的剪应变增量云图Fig.3 Retaining wall shear strain contour using SSR

图4 挡墙内点安全系数分布等值图Fig.4 Contour map of point safety factor within wall

本文在进行强度折减法计算时采用的是 FLAC3D软件自带的solve fos 模块，计算耗时近1.5 h。采用点安全系数法时，耗时约20 min。可见：采用点安全系数可以有效地节约计算资源。主要原因在于强度折减法需要进行多次试算，直到挡墙达到临界状态为止，而点安全系数法只需在模型静力平衡计算结果的基础上调用FISH函数即可。

设筋材的允许拉应变[ε]=0.05，利用式(6)编写FISH函数计算筋材的点安全系数。图5所示为各层筋材的点安全系数等值线图。由于加筋土挡墙筋材拉应力分布的非线性，沿筋长方向上筋材的点安全系数也为非线性分布，并且各层筋材最小安全系数所在位置也不相同；随着挡墙高度增加，其位置向挡墙内部转移。各层筋材单元的最小点安全系数见表 3。从表 3可见：挡墙内抗拉安全系数最小的筋材为第3层，其抗拉安全系数为7.28；随着筋材所在高度的增加，其抗拉安全系数增大。

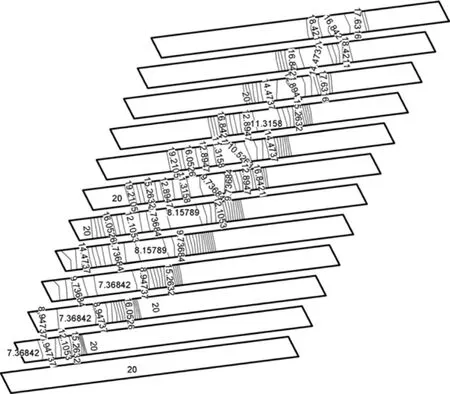
图5 筋带的抗拉点安全系数等值线图Fig.5 Contour map of tensile point safety factor of reinforcements

表3 筋带的抗拉与抗拔安全系数Table 3 Tensile and anti-pullout safety factors of reinforcements

图 6所示为筋土界面屈服的点安全分布等值线图。由图6可见：筋土界面的点安全系数分布规律要比筋材的抗拉点安全系数分布规律复杂；在筋长方向上，大多呈增大→减小→增大→减小的马鞍形。将筋材和筋土界面的点安全系数与相应单元X坐标分别用Table命令输出，可以获得加筋体锚固区和活动区的分界点，然后，根据式(9)可以计算各层筋材的抗拔安全系数，计算结果见表3。由表3可见：该加筋土挡墙抗拔安全系数最小的是第9层筋材，为8.97。

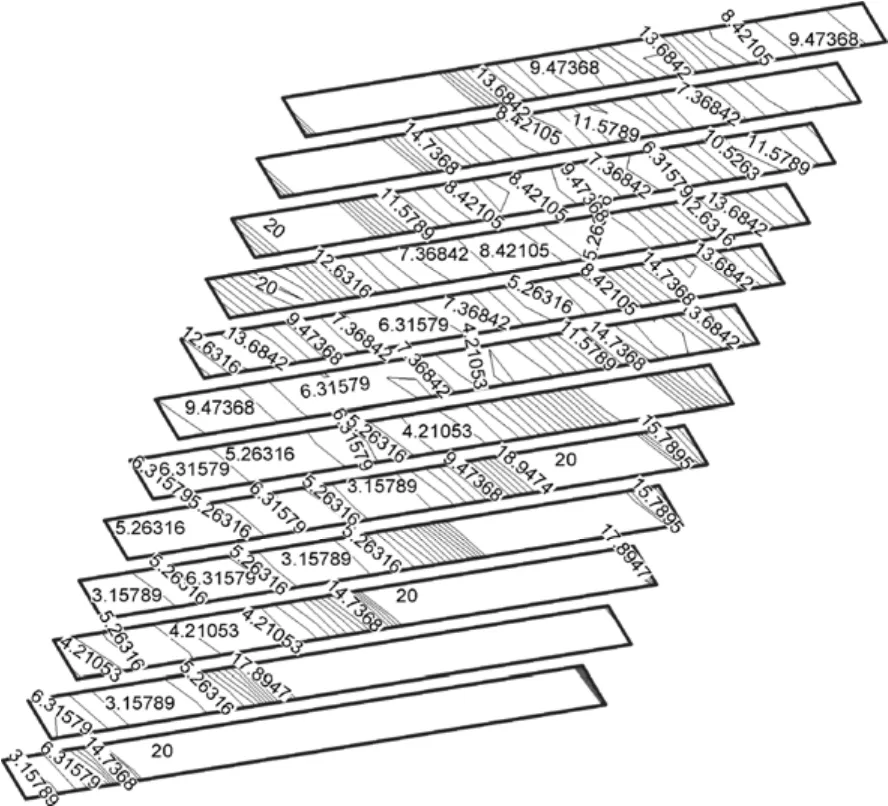
图6 筋土界面的点安全系数等值线图Fig.6 Contour map of point safety factor of interface between soil and reinforcements

4 结论

(1) 将点安全系数法用于加筋土挡墙的稳定性分析。在理论分析的基础上，推导了岩土体、筋材和筋土界面的点安全系数以及筋材的抗拉抗拔安全系数计算方法，给出了点安全系数法在 FLAC3D中实现的步骤和FISH命令。

(2) 采用点安全系数法不仅可以获得加筋土挡墙内各部位的安全状态，而且可以获得筋材的抗拉与抗拔安全系数，有利于对影响挡墙稳定性的薄弱环节进行分析，符合规范要求与工程技术人员评定加筋土挡墙稳定性的习惯。

(3) 采用强度折减法分析加筋土挡墙的稳定性可以获得挡墙的安全系数与潜大滑裂面的位置与形状，计算结果直观。但强度折减法不能反映筋材的抗拉与抗拔稳定性。

(4) 与强度折减法相比，点安全系数不需要多次试算，计算耗时要少得多，可以大大减少计算量。

[1] 包承纲. 土工合成材料应用原理与工程实践[M]. 北京: 中国水利水电出版社, 2008: 2-5.BAO Chen-gang. The principle and application of geosynthetics in engineering[M]. Beijing: China Water Power Press, 2008:2-5.

[2] 姚胜利, 李强. 基于临界滑动场的加筋土边坡稳定性分析[J].路基工程, 2010, 4: 140-142.YAO Sheng-li, LI Qiang. Analysis on reinforced soil slope stability based on critical sliding Field[J]. Subgrade Engineering,2010, 4: 140-142.

[3] 李强, 朱大勇. 加筋土边坡临界滑动场[J]. 防灾减灾工程学报, 2010, 30(4): 431-434.LI Qiang, ZHU Da-yong. Critical slip field of reinforced soil slope[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010, 30(4): 431-434.

[4] 范鹏贤, 陈灿寿, 黄育. 加筋土边坡稳定性分析的水平条分法[J]. 岩土工程技术, 2010, 24(2): 55-57, 97.FAN Peng-xian, CHEN Chan-shou, HUANG Yu. Limit equilibrium method for reinforced slope based on horizontal slice[J]. Geotechnical Engineering, 2010, 24(2): 55-57, 97.

[5] 莫介臻, 周世良, 何光春, 等. 加筋土挡墙潜在破裂面模型试验研究[J]. 铁道学报, 2007, 29(6): 69-73.MO Jie-zhen, ZHOU Shi-liang, HE Guang-chun, et al. Study on potential failure surface model of reinforced soil retaining walls[J]. Journal of the China Railway Society, 2007, 29(6):69-73.

[6] 刘华北, Ling H I. 土工格栅加筋土挡土墙设计参数的弹塑性有限元研究[J]. 岩土工程学报, 2004, 26(5): 668-673.LIU Hua-bei, Ling H I. Elsto-plastic finite element study for parameters of geogrid-reinforced soil retaining wall[J].Chinese Journal of Geotechnical Engineering, 2004, 26(5): 668-673.

[7] 陈华, 赵有明, 张发春. 土工格栅加筋土挡墙施工工况有限元分析[J]. 重庆交通大学学报: 自然科学版, 2009, 28(6):1088-1091.CHEN Hua, ZHAO You-ming, ZHANG Fa-chun. Finite element analysis on geo-grid reinforced earth retaining wall at construction stage[J]. Journal of Chongqing Jiaotong University:Natural Science, 2009, 28(6): 1088-1091.

[8] 刘祚秋, 周翠英, 董立国. 边坡稳定及加固分析的有限元强度折减法[J]. 岩土力学, 2005, 26(4): 558-561.LIU Zuo-qiu, ZHOU Cui-ying, DONG Li-guo. Slope stability and strengthening analysis by strength reduction FEM[J]. Rock and Soil Mechanics, 2005, 26(4): 558-561.

[9] 连镇营, 韩国城, 孔宪京. 强度折减法研究开挖边坡的稳定性[J]. 岩土工程学报, 2001, 23(4): 407-411.LIAN Zhen-ying, HAN Guo-cheng, KONG Xian-jing. Stability analysis of excavation by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 406-411.

[10] 刘金龙, 栾茂田, 赵少飞. 关于强度折减有限元方法中边坡失稳判据的讨论[J]. 岩土力学, 2005, 26(8): 1345-1348.LIU Jin-long, LUAN Mao-tian, ZHAO Shao-fei. Discussion on criteria for evaluating stability of slope in elastoplastic FEM based on shear strength reduction technique[J]. Rock and Soil Mechanics, 2005, 26(8): 1345-1348.

[11] 王清, 陆新. 用有限元强度折减法进行加筋土挡土墙稳定性分析[J]. 后勤工程学院学报, 2006(1): 63-66.WANG Qing, LU Xin. Stability analysis on reinforced retaining wall by strength reduction of FEM[J]. 2006(1): 63-66.

[12] 钟国强, 周亦唐, 葛晓旭, 等. 用有限元强度折减法求加筋土挡墙的稳定安全系数[J]. 昆明理工大学学报: 理工版, 2003,28(1): 123-126.ZHONG Guo-qiang, ZHOU Yi-tang, GE Xiao-xu et al. Analysis on safety coefficient of reinforced earth walls with FEM reduction[J]. Journal of Kunming University of Science and Technology: Science and Technology, 2003, 28(1): 123-126.

[13] 李树忱, 李术才, 徐帮树. 隧道围岩稳定分析的最小安全系数法[J]. 岩土力学, 2007, 28(3): 549-554.LI Shu-chen, LI Shu-cai, XU Bang-shu. Minimum safety factor method for stability analysis of surrounding rock mass of tunnel[J]. Rock and Soil Mechanics, 2007, 28(3): 549-554.

[14] 蒋青青. 基于 Hock-Brown准则点安全系数的边坡稳定性分析[J]. 中南大学学报: 自然科学版, 2009, 40(3): 786-790.JIANG Qing-qing. Stability of point safety factor of slope based on Hoek-Brown criterion[J]. Journal of Central South University:Science and Technology, 2009, 40(3): 786-790.

[15] 陈星, 王乐华, 刘君健, 等. 基于 Mohr-Coulomb准则点安全系数的隧道围岩稳定分析[J]. 水电能源科学, 2010, 28(4):100-102.CHEN Xin, WANG Le-hua, LIU Jun-jian, et al. Stability analysis of tunnel surrounding rock based on mohr-coulomb point safety factor[J]. Water Resources and Power, 2010, 28(4):100-102.

[16] 杨涛, 周德培, 马惠民, 等. 滑坡稳定性分析的点安全系数法[J]. 岩土力学, 2010, 31(3): 971-975.YANG Tao, ZHOU De-pei, MA Hui-min et al. Point safety factor method for stability analysis of landslide[J]. Rock and Soil Mechanics, 2010, 31(3): 971-975.