永磁同步电机自适应滑模负载观测器研究

王志宇， 王长松， 齐昕， 周晓敏

(北京科技大学机械工程学院，北京 100083)

0 引言

高性能的交流伺服系统要求具备良好的动态性能和静态性能。在实际工作中，负载转矩突变会对系统运行状态造成影响，同时转矩又是难以直接测量的非电物理量，所以提高伺服系统的抗负载转矩扰动能力成为近年来的一个研究热点。

文献［1］用改进的扩展Kalman滤波器进行负载转矩的辨识;文献［2］建立了基于Kalman滤波器的负载转矩观测器，根据测量的电流、机械位置和转速等参数对负载转矩进行估计;文献［3－4］基于电机数学模型，设计了降阶状态观测器对负载转矩进行辨识，并用辨识结果对速度变化进行在线补偿，提高了系统的鲁棒性;文献［5］采用高阶滑模控制技术和滑模微分器设计了对扰动转矩观测器，将估计反馈到控制系统中，使负载变为确定输入量，减小了对系统运动的影响;文献［6］讲述了负载转矩观测器在高速列车驱动系统中的应用;文献［7］用反馈线性化控制方法对系统的负载扰动进行估计，通过对系统控制量在线补偿，提高了系统的运行质量。

本文提出了一种MRAS和滑模变结构理论相结合的负载观测器，用于在线为转速调节器提供转矩变化的信息，经仿真实验表明，观测器工作稳定可靠，能提高调速系统的鲁棒性。

1 PMSM数学模型

理想电机模型的假设条件为:

忽略电动机铁心的饱和，忽略漏磁通的影响，不计电动机中的涡流和磁滞损耗，电动机的电流为对称的三相正弦波电流，且转子磁链在气隙中呈正弦分布。转子定向d－q旋转坐标系的转速数学模型为

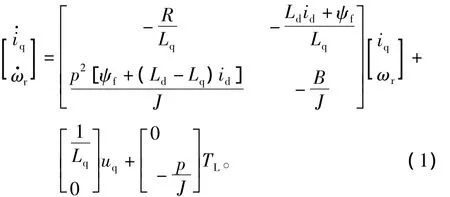
当采用id=0的矢量控制时，上式可以简化为

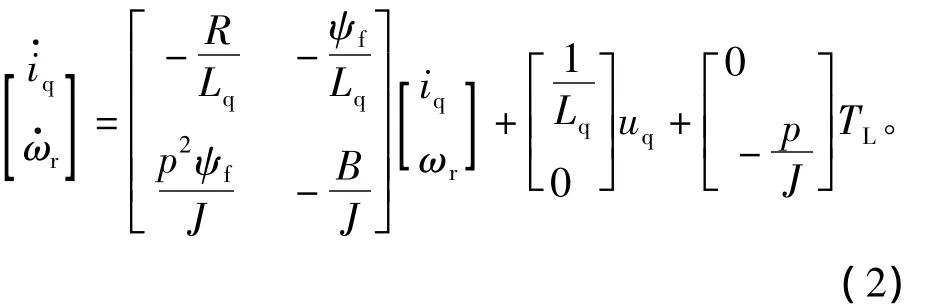
式中:uq，iq为定子电压电流d、q轴分量;R为定子绕组电阻;Lq为交轴电感;p为磁极对数;ψf为转子永磁体磁通;ωr为转子电气角速度;B，J为阻力摩擦系数和转动惯量。

2 自适应滑模负载观测器的设计

2.1 变结构控制的基本原理

变结构控制是前苏联学者Emelyanov、Utkin和Itkin在20世纪60年代提出的一种设计方法［8］。基本思想是根据状态偏差的极性和大小，使反馈信号的极性或大小作相应的改变，从而使得控制器从一种结构切换为另一种结构，以达到一定的控制性能要求，所设计出的控制器的形式为

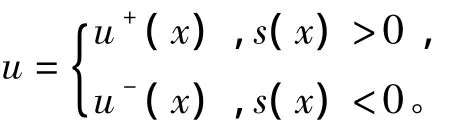
其中，u+(x)≠u－(x)，s(x)=0 为切换超平面，选择原则是保证最终滑动模态的稳定性及动态品质。

2.2 基于MRAS的永磁同步电机负载转矩辨识的原理

2.2.1 Popov超稳定理论

超稳定理论是将系统分为前向的线性定常方块和反馈的非线性方块，当前向方块的传递函数正实时，根据超稳定理论给出的反馈方块的参数自适应律可以保证系统的稳定性。

2.2．2 负载转矩的辨识原理

在id=0的永磁同步电机矢量控制系统中，选用dq旋转坐标系的转速方程作为转矩辨识模型。利用可调模型和参考模型输出量的误差构成自适应率来实时调节可调模型的负载转矩估计值，当估计值趋近真实值时，两模型的状态变量值近似相等。永磁同步电机负载转矩辨识的模型框图如图1所示。

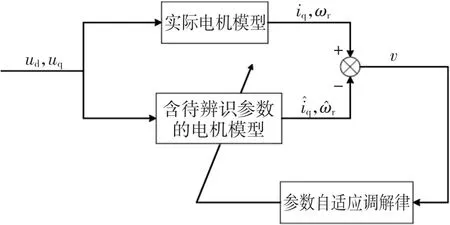
图1 基于MRAS的永磁同步电机转矩辨识原理图Fig．1 Load torque identification principle diagram

2.3 基于MRAS的自适应滑模负载转矩观测器的设计

2.3.1 误差状态方程的构造

将永磁同步电机转速方程作为辨识的参考模型为

构造参数可调的估计模型为

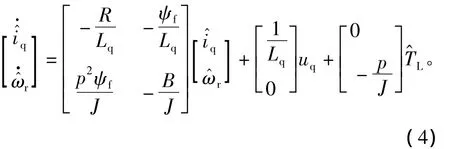
定义状态误差为

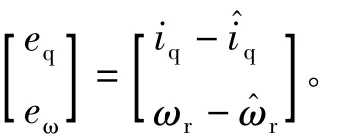
式(3)减式(4)得误差状态方程为

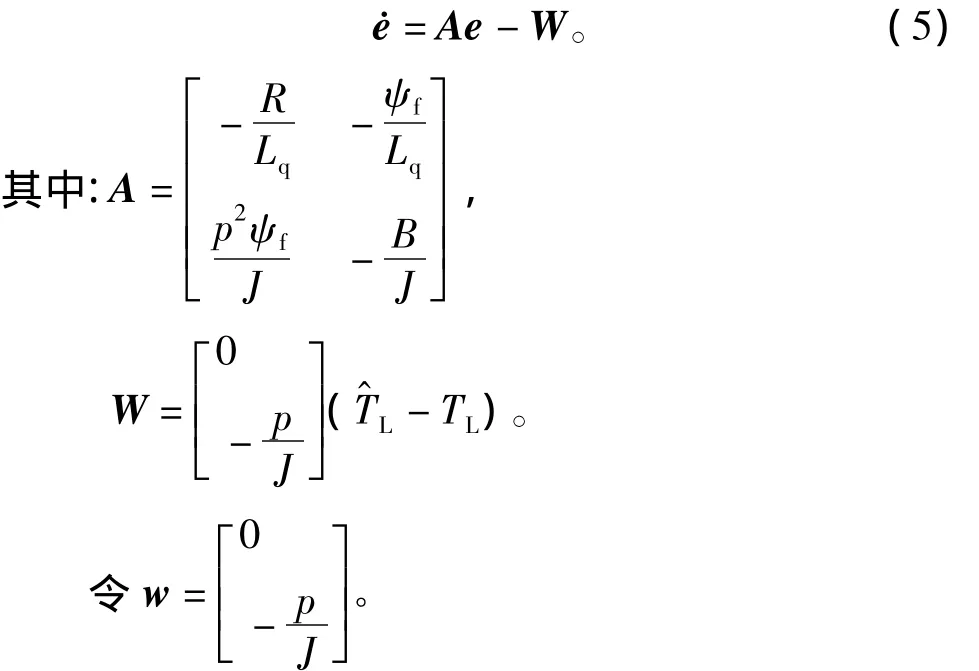
则辨识系统等效为一个非线性反馈系统，如图2所示。

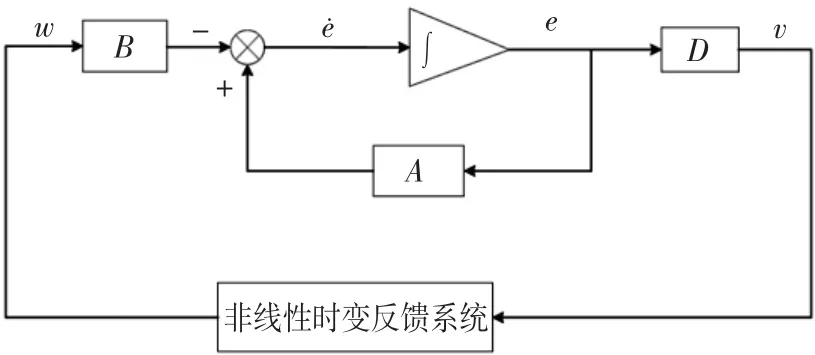
图2 等效非线性反馈系统Fig．2 Equivalent nonlinear feedback block diagram

根据Popov超稳定理论，要使上述系统稳定，则要求下列条件成立:

1)线性定常环节严格正实，即传递矩阵H(s)=(sI－A)－1为严格正定矩阵;

2)非线性时变环节满足Popov积分不等式。

在同步电机的辨识系统中，传递矩阵H(s)=(sI－A)－1一般满足严格正定的条件，取B=D=I。再根据Popov积分不等式，有

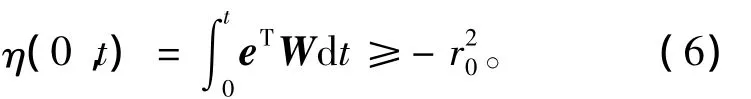
求解参数自适应律，为任一有限正数。

由Popov超稳定理论可得，eTw是负载转矩估计值与实际值误差的线性函数，即

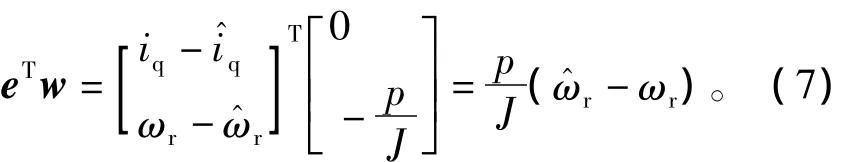
2.3.2 滑模面的设计

选择负载转矩估计值与实际值误差为零的曲线作为滑模面，为提高稳态调节精度，引入积分项，则滑模面方程为

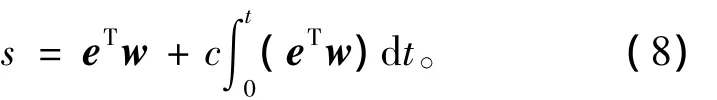
将式(7)代入得

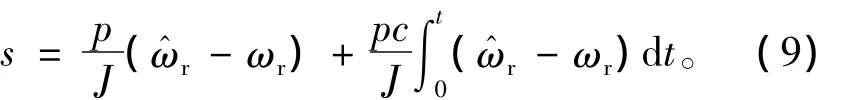
2.3.3 负载转矩观测值的计算

指数趋近律s=－ks－εsign(s)不但能保证状态轨迹到达滑动面，还可以通过选择ε和k来保证到达运动的响应品质，同时按指数趋近律进行的设计自然满足到达条件ss＜0，所以选择指数趋近律设计滑模观测器。

对滑模面求导得

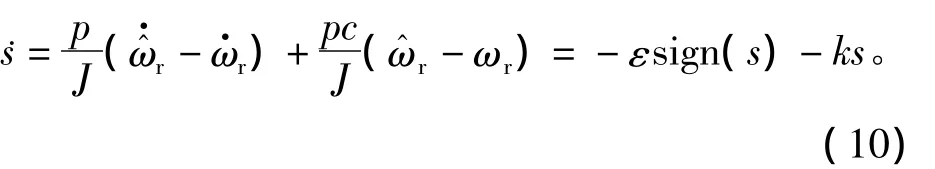
将状态方程和滑模面方程代入得

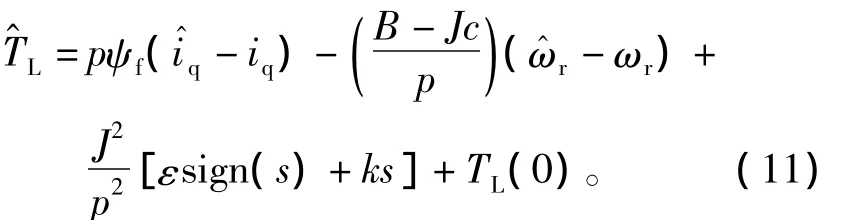
其中，因系统负载转矩TL是一个未知的时变的物理量，所以用零时刻负载转矩的估计值TL(0)替代。

2.4 观测器参数设计

在滑模转矩观测器中共有积分时间常数c，趋近律的常数ε和k三个参数，参数取值是否恰当对系统性能有影响。

2.4.1 滑模面积分时间常数的选择

滑模面中积分环节的作用是消除转速的稳态误差，提高控制精确度。但在启动或调节器的给定转速大幅度变化时，短时间内系统输出有很大的偏差，如积分时间常数选择不合适，则会产生大的超调量，同时对转速调节的精确度也有影响。

这里参考PID控制中的积分分离思想设计滑模面的积分时间常数，即当偏差(－ωr)较大时，令积分时间常数为0，取消积分作用;当偏差－ωr)小于设定阈值时，引入积分控制，根据转速差的绝对值和设定的阈值决定积分时间常数的取值。

2.4.2 趋近律常数ε和k的选择

一般来说，k决定了收敛到滑动面的速度，当s的绝对值较大时，大的k值可加快转速值的收敛速度;ε决定了抖振的幅值。所以理论上讲k的取值应大些，ε的取值要小些。

转矩观测器的抖振主要体现在输出量ωr的变化上，它的大小影响着负载转矩的估计值，从计算公式可看出ε作用到上的量为，远远小于TL的变化量，所以ε取值范围较大，一般小于20即可。

在一定范围内，k的取值越大变化的速度越快，表现为转速变化的响应速度快，在实际应用中，可根据电机的初始负载转矩，额定负载转矩和可能的最大负载转矩，利用的计算公式进行简略计算，以确定k的初始值。

依据以上的推导过程建立负载观测器模型，如图3所示。

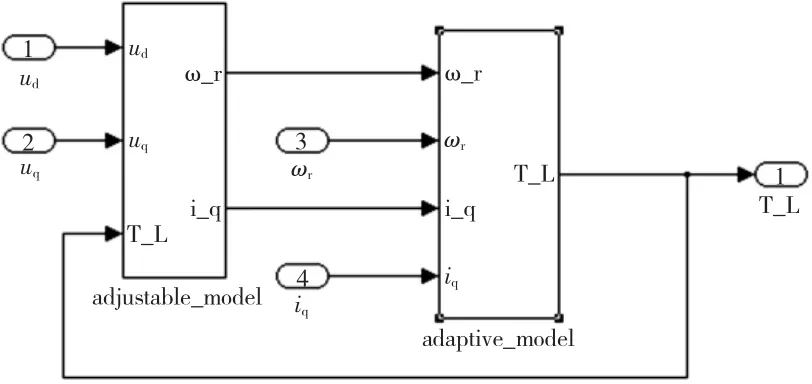
图3 负载转矩观测器模块Fig．3 Load torque observer block diagram

3 仿真实验及分析

为了验证负载转矩观测器模块的有效性，在转速电流双闭环矢量控制系统中进行了仿真研究。

永磁同步电机的参数为:额定电压为560 V;额定电流为36 A;额定转速为3 000 r/min;额定转矩为20 N·m;定子每相电阻0.1 Ω;d轴电感为0.000 425 H;q轴电感为0.001 25 H;极对数为4;转动惯量为0.002 2 kg·m2;转子磁链为0.111 9 Wb。

实验共有两个，系统原理图如图4所示。

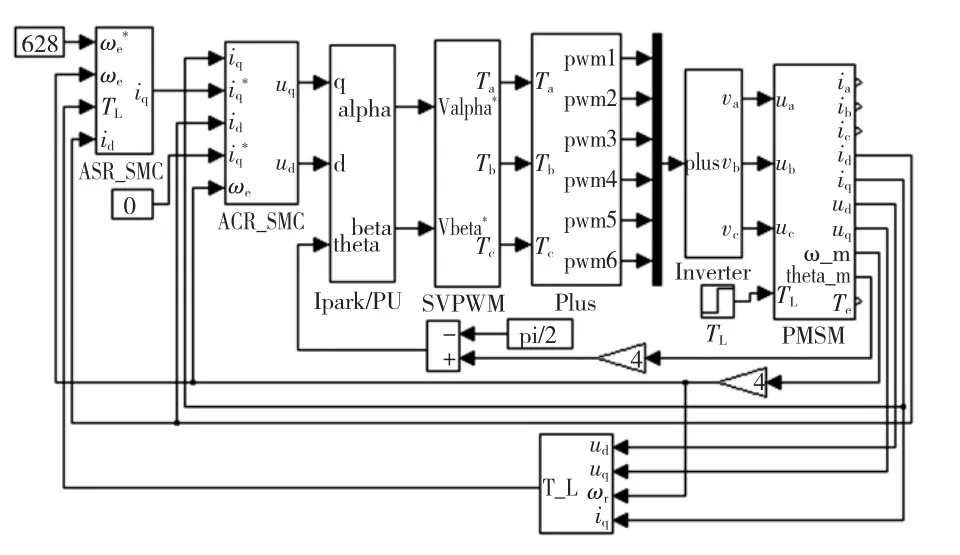
图4 PMSM矢量控制系统图Fig．4 The simulation configuration of PMSM drive system

3.1 仿真实验

3.1.1 实验一

实验目的:通过比较系统转速调节情况，说明负载观测器对于高质量调速系统的必要性。

实验内容:电机带负载TL=8 N·m，运行于628 rad/s，在第0.08 s负载转矩跳变为TL=9 N·m，0.1 s后，电机负载又回到TL=8 N·m。

图5中虚线表示外加负载的变化过程，实线为负载观测器对外负载的辨识结果。

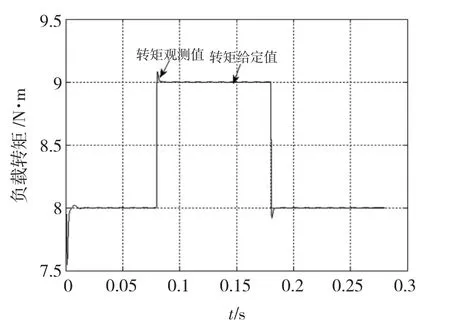
图5 负载转矩辨识结果Fig．5 The identification result of load torque

由图可知，负载转矩观测器能快速准确的观测出系统所加的初始负载转矩和运行过程中负载转矩发生的变化。

图6中实线为有负载观测器的调速系统转速变化曲线，其中初始负载TL(0)为估计值;虚线代表无观测器系统的转速变化，在计算过程中，初始负载按已知量处理TL(0)=8 N·m。

图6 负载转矩跳变后转速调节情况的对比Fig．6 The comparison of speed adjusting course

由图可知，在启动阶段，系统转速能在0.02 s内稳定于设定值;

运行过程中负载转矩变化，观测器将辨识结果反馈给速度控制器，经0.02 s的调节使转速恢复到原状态;而无观测器的系统，因不能辨识出转矩的变化，速度产生了较大幅度的波动，在控制器的调节下经过0.07 s，转速才又恢复到设定值。

从图6反映出的信息可知，在调速系统中引入负载观测器是必要的。

3.1.2 实验二

实验目的:检验负载转矩观测器工作的动态特性和具有负载转矩观测器的调速系统对转矩变化的鲁棒性。

实验内容:电机带负载TL=2+0.8sin(62.8t)N·m，运行于628 rad/s，在第0.1 s加载TL=4+0.8sin(62.8t)N·m持续时间为0.006 s的干扰，在第0.2 s负载转矩跳变为TL=3+0.6sin(125.6t)N·m。

图7中虚线表示负载转矩的变化，实线为观测器对负载转矩变化的观测结果。

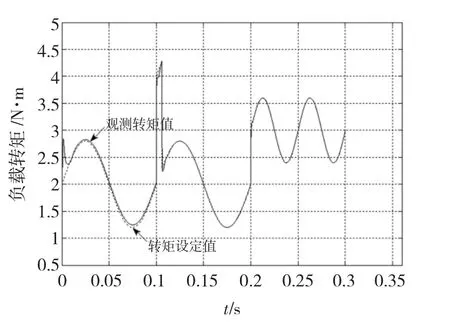
图7 负载观测结果Fig．7 The result of load torque observer

由图可知，观测器能准确辨识出负载转矩的变化和突加干扰。

图8为负载变化时转速调节结果。由图8可知，在启动阶段，系统转速未受波动的负载转矩很大影响，仍能在0.02 s内稳定到设定值;

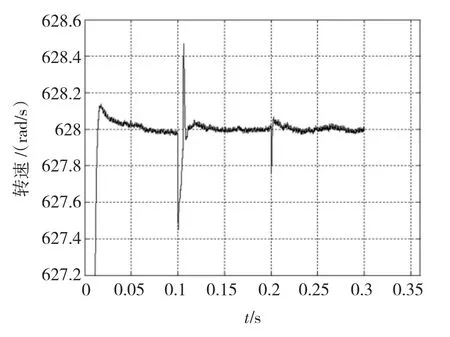
图8 负载变化时转速调节结果Fig．8 The adjusting process of rotor speed

运行过程中，在发生干扰和负载转矩跳变后，依靠负载转矩观测器实时反馈的辨识结果，系统转速能很快的稳定于设定值。

4 结语

以Popov超稳定理论为辨识的理论基础，以滑模变结构控制作为计算方法，建立了负载转矩观测器，用于转速电流双闭环调速系统中，仿真实验表明，观测器能及时准确地检测出负载转矩的变化，从而提高调速系统的动态性能。

［1］AKRAD A，HILAIRET M，DIALLO D．Performance enhancement of a sensorless PMSM drive with load torque estimation［C］//IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society，November 7 －10，2010，Phonenix，AZ，USA．2010:945－950．

［2］ZHENG Zedong，FADEL M，LI Yongdong．A high-performance control system of PMSM based on load torque observer［C］//2007 IEEE Power Electronics Specialists Conference，July 8 － 12，2007，Orlando，Florida，USA．2007:587－592．

［3］陈荣，邓智泉，严仰光．基于负载观测的伺服系统抗扰研究［J］．中国电机工程学报，2004，24(8):103－108．

CHEN Rong，DENG Zhiquan，YAN Yangguang．Research on resist-disturbance performance of servo system based on load observer［J］．Proceeding of the CSEE，2004，24(8):103－108．

［4］鲁文其，胡育文，梁骄雁，等．永磁同步电机伺服系统抗扰动自适应控制［J］．中国电机工程学报，2011，31(3):75 －81．

LU Wenqi，HU Yuwen，LIANG Jiaoyan，et al．Anti-disturbance adaptive control for permanent magnet synchronous motor servo system［J］．Proceeding of the CSEE，2011，31(3):75 －81．

［5］皇甫宜耿，刘卫国，马瑞卿．永磁同步电机高阶滑模控制与扰动转矩估计［J］．西北工业大学学报，2009，27(5):630 －634．

HUANGFU Yigeng，LIU Weiguo，MA Ruiqing．High order sliding mode control for a PMSM with disturbance torque estimation［J］．Journal of Northwestern Polytechnical University，2009，27(5):630－634．

［6］Guzinski J，Abu-Rub H，Diguet M，et al．Speed and load torque observer application in high-speed train electric drive［J］．IEEE Transactions on Industrial Electronics，2010，57(2):565 －574．

［7］刘栋良，严伟灿，赵光宙．基于转矩扰动估计的电机反馈线性化控制［J］．电力系统及其自动化学报，2005，17(5):60－63．

LIU Dongliang，YAN Weican，ZHAO Guangzhou．Feedback linearization control of motor with torque disturbance estimation［J］．Proceedings of the CSU-EPSA，2005，17(5):60 －63．

［8］王庆龙，张崇巍，张兴．交流电机无速度传感器矢量控制系统变结构模型参考自适应转速辨识［J］．中国电机工程学报，2007，27(15):70 －74．

WANG Qinglong，ZHANG Chongwei，ZHANG Xing．Variablestructure MRAS speed identification for speed sensorless vector control of induction motor［J］．Proceeding of the CSEE，2007，27(15):70－74．