mkdv方程的精确行波解

薛春荣

(渭南师范学院数学与信息科学学院，陕西渭南714000)

0 引言

随着科学技术的发展，非线性现象在自然科学和社会科学领域的作用越来越重要，物理、化学、生物、工程技术，甚至社会的经济问题都存在着大量的非线性问题，这些问题的研究常常能用非线性偏微分方程来描述.因此如何求解这些非线性方程成为广大数学和物理工作者致力于研究的一个课题.近年来，人们提出和发展了求解非线性方程的有效方法.如齐次平衡法［1－2］，双曲正切函数展开法［3－5］，并用这些方法求解了许多非线性方程.

本文推广了已被人们广泛使用的双曲函数方法，并利用该方程求解mkdv方程［6］.

很显然，各种重要的非线性演化方程如kdv方程，kdv-mkdv方程，mkdv-Burgers方程，都是方程

的特殊情形.我们通过求解方程(2)来介绍这种方法，并利用这种方法对(1)进行求解.

1 Kdv-mkdv-Burgers方程的精确行波解

Kdv-mkdv-Burgers方程：ut+ αuut+ βu2ux+ γuxx+ δuxxx=0

假定u(ξ)=.其中函数 f(ξ) 可取为：f(ξ)=tanhξ，f(ξ)=cothξ，f(ξ)=tanξ，f(ξ)=cotξ，系数Ai(i=1，2，…m)为待定常数.把(5)式代入方程(2)，通过平衡方程的线性最高阶导数项uξξξ和非线性项uuξ的阶数，可以确定行波解的阶数m. (5)

把(6)式代入(4)式中，可得到一组确定常数A0，A1，K，和ω的方程

由于方程(8)和(9)相同，都是共有4个未知数，而只有3个独立方程，选取ω为自由参数，如果δ＞0，β ＜ 0，ω或 δ＜ 0，β ＞ 0，ω ＞则A，A和K有实解.解(8)或(9)，得到01

把(10)代入(6)和(3)，由于tanh(－ ξ)= －tanhξ，coth(－ ξ)= －cothξ，得到组合Kdv-mkdv-Burgers方程的4个精确行波解

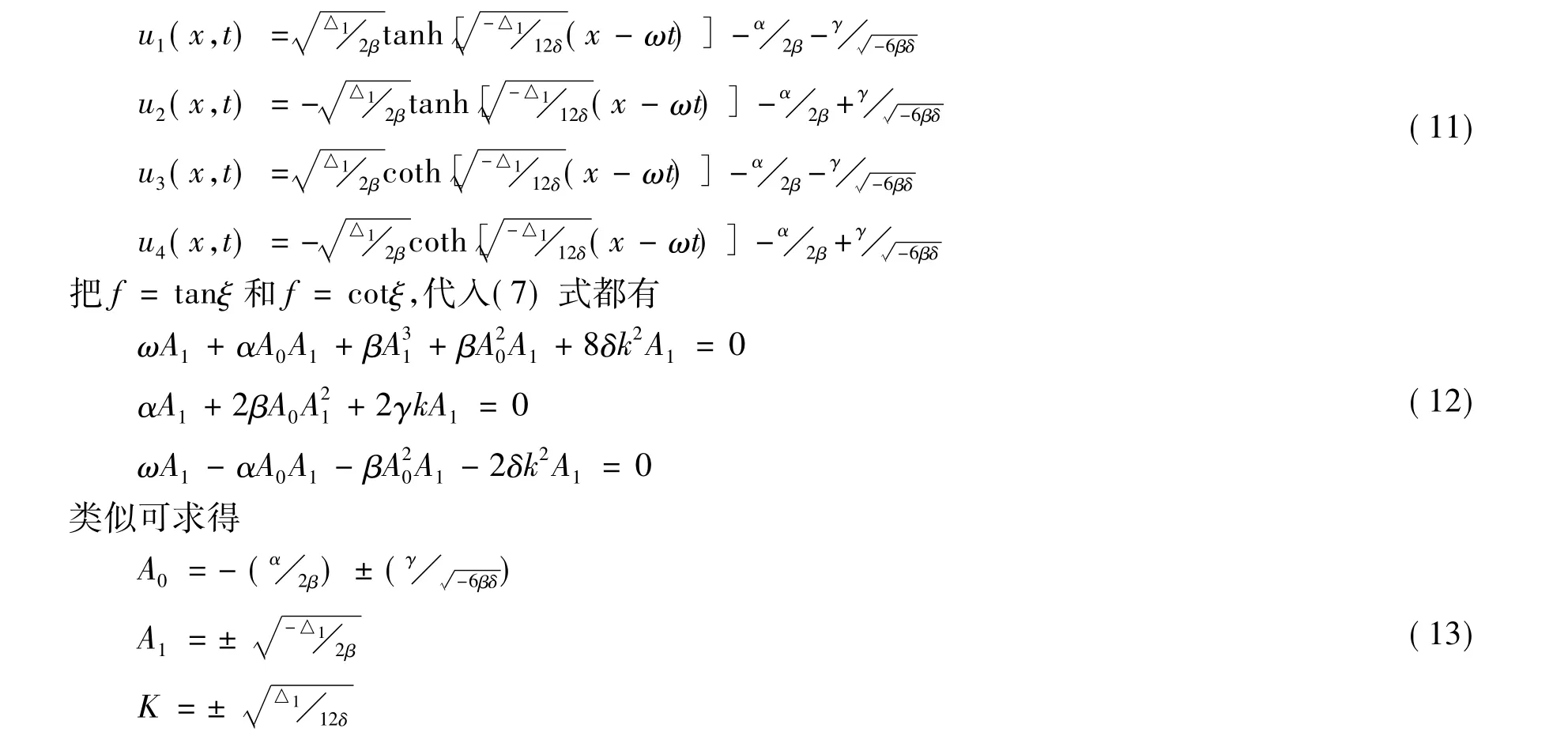
将(13)代入(6)和(3)，于是我们又得到组合Kdv-mkdv-Burgers方程的4个精确行波解

2 mkdv方程的精确行波解

把 u(x，t)=u(ξ)=u［k(x － ωt)］代入方程(1) 得到

假定u(ξ)=其中函数 f(ξ) 可取为：f(ξ)=tanhξ，f(ξ)=cothξ，f(ξ)=tanξ，f(ξ)=cotξ，系数Bi(i=1，2，…，m)为待定常数.把(16)式代入方程(1)，通过平衡方程的线性最高阶导数项和非线性项的阶数，可以确定行波解的阶数m.m+3=3m+1，故m=1. (16)

由于方程(19)和(20)相同，都是共有4个未知数，而只有3个独立方程，选取ω为自由参数，如果ω＞0，则 B0，B1，k有实数解，解(19) 或(20) 得

将(21) 代入到 (17)和(3)，由于tanh(－ ξ)=tanhξ，coth(－ ξ)= － cothξ，得到mkdv方程的4个精确行波解

将(24)代入到(17)和(3)，于是我们又得到mkdv方程的4个精确行波解

3 结论

利用一种推广的直接方法，求出mkdv方程的多类精确行波解.很显然，本文方法也可以用来处理(2+1)维组合Kdv-mkdv-Burguers方程

(ut+ αuux+ βu2ux+ γuxx+ δuxxx)x+ ηuyy=0

和Kolmogorov-Petrovski-Piskunov方程(ut－uxx+μu+νu2+λu3)x+δuyy=0的精确行波解.

［1］Wang M.L.Solitary Wave solution for Boussinesq equations［J］.Phys.Lett.A，1995，199：162-172.

［2］Fan E.G，Zhang H.Q.The Homogeneous balance method for solving nonlinear soliton equation［J］.Acta.Phys.Sin，1998，44：353-370.

［3］Parkes EJ，Duffy BR.Velling solitary Wave solutions to a compound kdv-Burgers Equation［J］.Phys.Lett.A，1997，229：217-220.

［4］Fan E G.Extended tanh-function method and its applications to nonlinear equations［J］.Phys.Lett.A，2000，277：212-218.

［5］李志斌，张善卿.非线性波方程准确孤立波解的符号计算［J］.数学物理学报，1997，17(1)：81-89.

［6］Lou S.Y，Huang G.X，Ruan H.Y.Exact solitary waves in a convecting fluid［J］.J.Phys.A;Math.Gen，1991，24：587-590.