一种基于概率的覆盖粗糙集模型研究

王小改，李巧艳，王 璐

(西安工程大学理学院，西安710048)

0 引言

1982年波兰数学家Z.Pawlak首次提出了粗糙集理论［1］，这是一种处理不确定性和不精确性问题的新的数学工具，在数据挖掘、知识约简等方面得到成功的应用.1983年Zakowski［2］从实际应用出发，提出了覆盖粗糙集模型，并讨论了相关的性质.2003年William Zhu和WANG Fei-yue［3］在覆盖粗糙集的基础上给出了约简的概念和方法，证明了一个覆盖通过约简得到的最简覆盖是唯一的，并且证明了最简覆盖相同的两个覆盖产生相同的上、下近似.

1 一种基于概率的覆盖粗糙集模型

定义1［4］设U是有限论域，集函数P∶2U→［0，1］成为概率侧度，若

(1)P(U)=1，

(2)当A∩B=Ø，有P(A∪B)=p(A)+p(B)，

若P是U上的概率测度，称A，B⊆U且P(B) ＞0，称

为在事件B发生的情况下事件A发生的条件概率.

定义2 (覆盖、覆盖近似空间)设U是一个论域，C是U的一个子集族.如果C中的所有子集都不空，且∪C=U，则称C是U的一个覆盖，称有序对 ＜U，C＞为覆盖近似空间.

定义3［5］(最小描述)设 ＜U，C ＞ 为一个覆盖近似空间，x∈U，则称

为x的最小描述.

定义4 (覆盖下近似、上近似)设C={K1，K2，…，Kn}是论域U上的一个覆盖，P为定义在U的子集类构成的σ代数上的概率测度，记A=(U，C，P)为覆盖概率近似空间，则对任意X⊆U，0≤β＜α≤1，定义X的关于A=(U，C，P)依参数α，β的下近似和上近似分别为：

X 的关于 A=(U，C，P) 依参数 α，β，的覆盖边界域为 Bn(X，α，β)=

定理1 对于定义4下的覆盖上、下近似有如下性质：

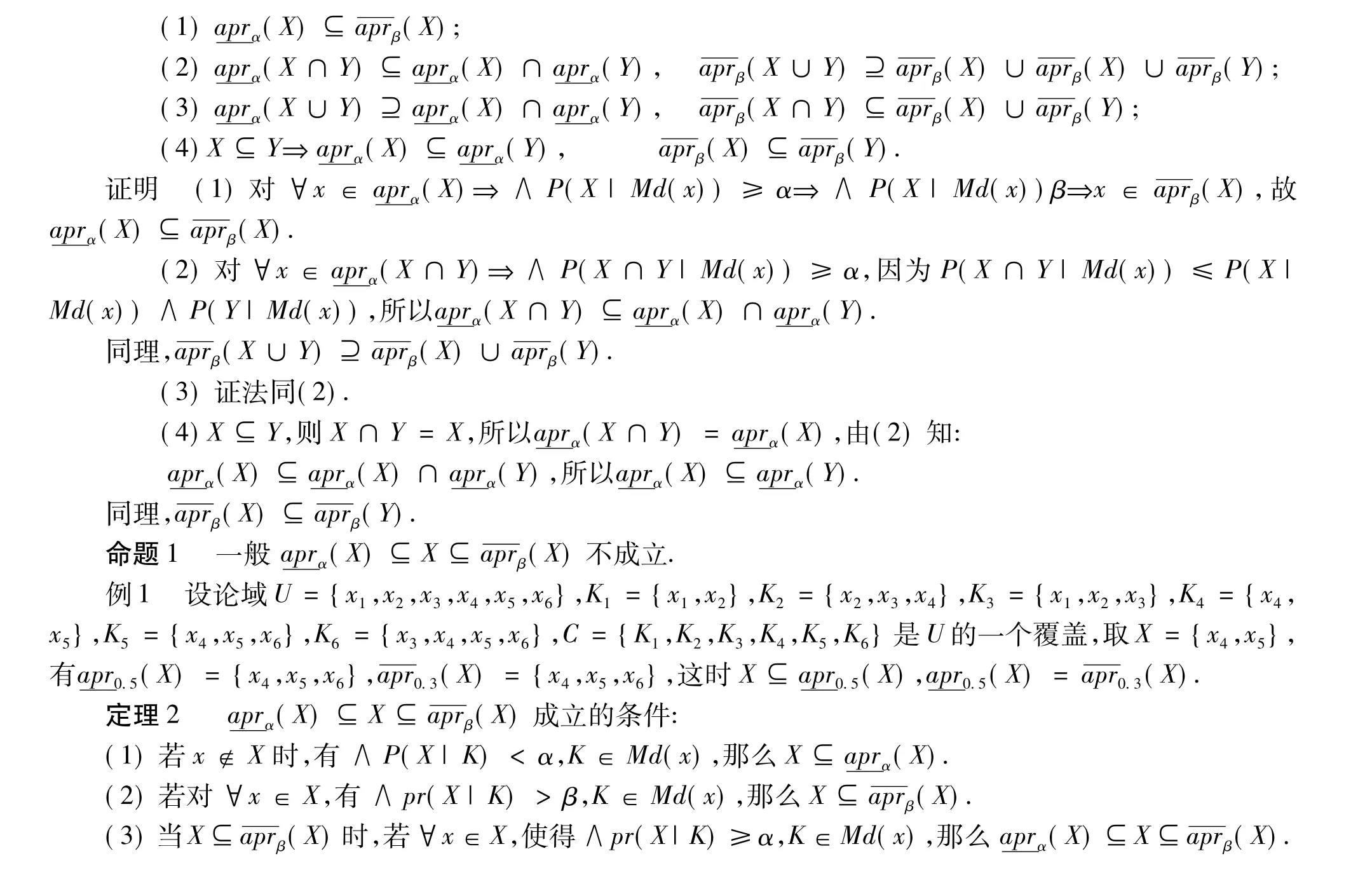
2 覆盖粗糙集的数字特征

文献［6］介绍给出了粗糙集的数字特征.本节我们在文献［6］的基础上讨论定义4给出的覆盖粗糙集的数字特征.

定义5 (集合的近似精度和粗糙度)设C是论域U上的一个覆盖，对∀X⊆U，称集合X的α近似精度和ρ粗糙度分别为

对每一个X⊆U，有0≤α(X)≤1.当α(X)=1时，X的边界域为空集，所以集合X是可定义的;当α(X)＜1时，集合X有非空的边界域，所以集合是不可定义的;当集合X为空集时，我们就定α(X)=α(Ø)=1.

X的α粗糙度与ρ近似精度恰恰相反，它反映了我们在覆盖C对于集合X表达的范畴了解的不完全程度.

定义6 (近似分类精度和近似分类质量)设C是论域U上的一个覆盖，以及论域U上的一个划分π(U)={X1，X2，X3，…，Xn} ∈ Π(U)，且这个划分独立于覆盖 C.其中子集 Xi(i=1，2，…，n) 是划分π(U)的等价类.首先定义π(U)的下近似和上近似分别为：

定义7 (知识库中系统参数的重要度)设C是论域U上的一个覆盖，C表示描述覆盖近似空间 ＜U，C＞的一组数或单个的系统参数.∀X⊆U和独立于系统参数C的论域U的一个划分π(U)={X1，X2，…，Xn}，定义集合X关于系统参数C的重要度和划分π(U)关于系统参数C的重要度分别为

由定义，系统参数具有以下性质：

(1)∀X⊆U，π(U)∈∏(U)，0≤sigC(X)≤1;0≤sigC(π(U))≤1.

(2)当sigC(X)=1时，表明覆盖C可精确描述出集合X.

(3)当sigC(X)=0时，表明覆盖C无法判断论域U中的任意元素是否属于概念X.

(4)X系统参数C的重要度越大，表明用覆盖C描述集合X的近似精度就越高.

(5)当sigC(π(U))=1时，表明覆盖C可精确描述出划分π(U)，即划分π(U)是比覆盖C所表示的划分更粗的划分.

(6)当sigC(π(U))=0时，表明覆盖C无法判断论域U中的任意元素是否属于划分π(U)中的概念Xi(i=1，2，…，n).

(7)划分π(U)系统参数C的重要度越大，表明用覆盖C描述该划分π(U)的似精度就越高.

(8)无论集合还是划分，它的系统参数C的重要度越大，表明覆盖C分类能力越强.

(9)无论集合还是划分，它的系统参数C的重要度随着C的细划而单调递增.

3 覆盖粗糙集的拓扑特征

定义8 设C是论域U上的一个覆盖，

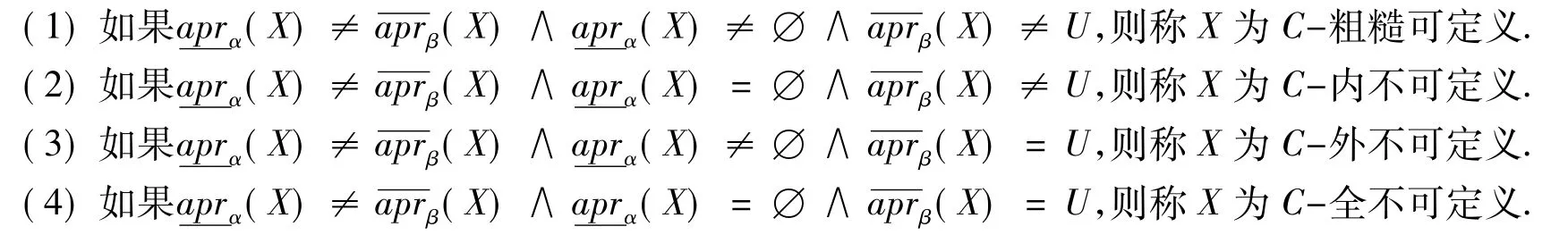
定理3 (1)集合X为C-可定义，或C-粗糙可定义，或C-全不可定义，当且仅当 ～X为C-可定义的，或C-粗糙可定义，或C-全不可定义;

(2)X为C-外(或内)不可定义当且仅当 ～X为C-外(或内)不可定义.

所以X为C-粗糙可定义⇔ ～X为C-粗糙可定义.

综上所述，集合X为C-可定义，或C-粗糙可定义，或C-全不可定义，当且仅当 ～X为C-可定义的，或C-粗糙可定义，或C-全不可定义.

同理可证(2)成立.

4 结语

本文提出了一种新的覆盖粗糙集的上、下近似定义，并讨论了其性质.同时，研究了其数字特征与拓扑特征，丰富了覆盖粗糙集的研究.

［1］Pawlak Z.Rough sets［J］.International Journal of Computer and Information Sciences，1982，11：341 －356.

［2］Zakowski W.Approximation in the space(U，∏)［J］.Demonstration Mathematic，1983，16：761 －769.

［3］William Zhu，WANG Fei-yue.Reduction and axiomization of covering generalized rough set［J］.Information Sciences，2003，152：217 －230.

［4］孙秉珍，巩增泰.变精度概率粗糙集模型［J］.西北师范大学学报(自然科学版)，2005，41(4)：23－26.

［5］Zhu W，Wang F Y.Reduction and axiomization of covering generalized rough sets［J］.Information Sciences，2003，152：217 －230.

［6］苗夺谦，李道国.粗糙集理论、算法与应用［M］.北京：清华大学出版社，2008.34－57.