赋权图的最小环路遍历路径分析与研究

索红军

(渭南师范学院数学与信息科学学院，陕西渭南714000)

0 引言

图是一种多对多的复杂的网状数据结构，当给图的各条边赋予具有一定实际意义的数值时，就成为赋权图(也称为网)，赋权图是解决一些实际问题的非常有效的工具.赋权图中两顶点之间的最短路径、赋权图的最小生成树等都与解决实际问题密切相关.在此，我们提出应用赋权图解决环路访问的最小代价问题研究.

1 问题的提出

在赋权图中，研究过图的遍历、最小生成树、最短路径［1］、哈密尔顿回路［2］等很多方面.其中图的遍历要求从图的一个顶点开始，访问完所有顶点且每个顶点只能访问一次即可，图的最小生成树只要求各顶点之间有通路且路径的权值之和最小即可，最短路径研究的是两顶点间的路径，哈密尔顿回路要求每个顶点只能访问一次.然而现实问题中存在与哈密尔顿回路和最短路径相似但又不同的问题，即从图中某一顶点出发，访问完所有的顶点后又要回到起点，例如快递员从快递公司出发送完货物后又要回到快递公司等.这样的问题不同于传统旅行商问题［3］，不要求每个顶点只到达(访问)一次，也不完全等同于中国邮递员问题［2］(欧拉回路)，不要求所有的边都走到，但必须要求访问完所有的顶点后，又要回到出发顶点，并且在整个过程中经过的边的权值之和最小.对于这样的问题，在比较庞大的赋权图中，目前还没有公认的比较好的完全解决方案.二边逐次修正法［4］等方案只能是寻找相对好遍历路径(不一定是最优路径)的解决方案.为了分析研究此类问题，提出以下定义：

赋权连通图的最小环路遍历路径：在一个赋权图中从某一顶点出发，沿图的边到达其他顶点，访问完所有的顶点后，又回到出发点，整个过程经过的边的权值之和最小.将该过程经过的顶点按顺序排列即为赋权连通图的最小环路遍历路径.

2 问题的分析

赋权图的最小生成树研究代价问题，这样的方法对于像架设通信线路、铺设管道等只要顶点之间有路径即可的问题比较适合，对于像运送货物等运送人员或车辆等必须返回到出发点的问题不适合，因为人员或车辆返回时同样需要代价，而按照最小生成树的路径访问完所有顶点并沿该路径回溯返回到出发点，在整个运送环节中代价一般都比较大.

图的遍历只要求访问完所有顶点，不关心代价问题.赋权图的遍历在不考虑代价的情况下可用深度优先搜索和广度优先搜索方法，其中应用深度优先搜索遍历时，当与某个顶点相关联的顶点访问完后，必须回溯到上一个顶点，当访问完所有顶点并回溯到出发点时，将回溯过程应用的边和访问走向下一个顶点应用的边同样看待，这时整个过程经过的顶点序列就是赋权连通图的环路遍历路径.现在将访问时走向下一个顶点应用的边和回溯时应用的边权值相加，就涉及到了赋权连通图的环路遍历及其代价问题.当访问完所有顶点又回到出发点，所有进入下一个顶点的边和回溯的边的权值相加，就得到了赋权图的环路遍历代价，但这个代价一般都较大，因为深度优先搜索遍历是严格按照回溯方式进行的，而图中存在环路，不需要通过回溯方式亦可进行遍历.如图1所示(图中带括号序号实线为访问顺序，带括号虚线为回溯顺序，不带括号数字为权值)，从A出发沿图中标明的实线序号访问并沿虚线返回，遍历完成后回到A，其权值总和为84，显然不是最小的，原因是访问顶点的顺序不同导致回溯经过的边次数较多;某些地方的回溯可以更改，不需要回溯可以减少费用.容易发现，当参考广度优先搜索遍历图的策略进行图的环路遍历时，其代价将会更高.故此可知，应用深度优先搜索和广度优先搜索方案均不能完成赋权图的最小环路遍历问题.

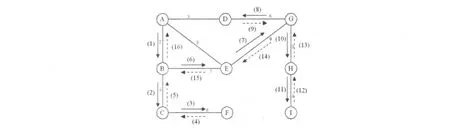
图1 图的深度优先搜索遍历

3 问题解决的分析与研究

经过分析，我们发现，参考深度优先搜索策略进行图的环路遍历，要使环路遍历总权值最小，应该从两方面考虑：首先不能按照深度优先搜索策略完全回溯，可以通过权值小的环路边取消一部分回溯;其次，若需要回溯，回溯的边权值尽可能小.如在图1所示的赋权图中，若按照图中顺序访问到顶点G时，先访问H、I，再回溯到G，然后访问D，再沿边＜A，D＞直接回到出发点A，其中减少了标号为9、14、15、16的回溯边，增加了边＜A，D＞，按照这样的路线访问总权值为63，实现了最小.

对于任意一个赋权连通图，如何进行环路遍历，使其总的权值尽可能小.依据狄杰斯特拉(Dijkstra)算法［5］，提出以下赋权连通图的最小环路遍历方案：

(1)确定始点V1(也是终点);

(2)应用狄杰斯特拉算法求出从始点 V1到其余各顶点 V2，V3，…，Vn的最短路径权值 Dist1－2，Dist1－3，…，Dist1－n以及相应的最短路径 Path1－2，Path1－3，…，Path1－n;

(3)在各最短路径权值 Dist1－2，Dist1－3，…，Dist1－n中查找最小路径值 Dist1－i，并求出 Vi到 V1的次短路径顶点序列Pathi－1;

(4)检查两个路径序列Path1－i和Pathi－1中是否包含赋权图的全部顶点，若已经全部包含，则这两个路径的顶点序列顺序即为在赋权连通图中要找的环路遍历路径.否则，保持Path1－i不变，求出Vi到V1的下一个次短路径顶点序列Pathi－1'，若路径序列Path1－i和Pathi－1'包含赋权图的全部顶点，则这两个路径的顶点序列顺序即为在赋权图中要找的环路遍历路径，若这两个路径仍然未包含完赋权图的全部顶点，继续检查下一个次短路径序列Pathi－1″，直到找到包含全部顶点的环路遍历路径或者Vi到V1的路径已经到达最大;

(5)若Vi到V1的路径已经到达最大时还未求出包含全部顶点的环路遍历路径序列，则从V1到Vi的次短路径开始，继续重复应用上述过程，求出从Vi到V1的下一个次短路径顶点序列并检查，直到找到赋权图中包含全部顶点的环路遍历路径序列为止.

经分析，该方案不一定能找到权值总和最小的环路遍历路径，但可以找到权值总和比较小的环路遍历路径，在实际应用中有一定的参考价值.同时比起二边逐次修正法等方法实现起来简单，容易理解，可以为相关的问题解决提供理论参考和借鉴.

4 结论

本文参考狄杰斯特拉(Dijkstra)算法，根据实际问题的具体情况，提出赋权连通图中最小环路遍历路径以及求解最小环路遍历路径的方案，为现实中最优行程方案设计及相关问题建立数学模型提供一定的理论基础，以供大家在处理分析类似问题时参考和借鉴.

［1］耿国华.数据结构［M］.北京：高等教育出版社，2005.

［2］乔维声.离散数学［M］.西安：西安电子科技大学出版社，2005.

［3］李飞，白艳萍.用遗传算法求解旅行商问题［J］.中北大学学报(自然科学版)，2007，28(1)：49－52.

［4］王缔.最佳旅行问题的一种求解方法［J］.科教文汇(上旬刊)，2011，(8)：1 －3.

［5］严蔚敏.数据结构［M］.北京：清华大学出版社，2011.10.