沉积地层系统三维实体模型构建方法

朱良峰 ，孙建中，张成娟

（1. 华东师范大学 地理信息科学教育部重点实验室，上海 200062；2. 中国科学院 上海高等研究院，上海 201203；3. 上海市城市化生态过程与生态恢复重点实验室，上海 200062）

1 引 言

沉积地层是一种常见的层状地质实体，构建沉积地层环境下的三维地质模型对实际的地质分析与工程设计具有很大的应用价值[1]。近10年来，国内外在沉积地层系统三维模拟方面开展了卓有成效的研究，相关的研究进展主要体现在建模数据标准化、三维实体模型表示方法、三维模型重构技术等3个方面。目前，沉积地层系统建模数据标准化、三维实体模型表示方法这两方面所涉及的问题已基本解决，并在学术界和工程界形成共识；而在三维地质模型重构技术方面，虽然提出了一些建模算法，但当前仍缺乏简单通用、高效自动的建模方法，亟需结合各种复杂的地质背景条件，对已有的构模方法进行优化、改进及验证工作。

工程钻探法是一种传统的地下空间信息获取方式，钻孔资料具有简单、直观、准确、详细的优点。基于钻孔数据的建模方法一直是沉积地层系统三维重构技术的主流，常用的有地层骨架构模法[2－3]、地层层位法[4]、钻孔-层面模型法[5]、地层纵向分块处理法[6]等。经过实际工程验证发现：现有的建模方法及实现算法都存在或多或少的缺陷，其中一个突出的问题就是这些方法缺乏合理完善的缺失地层处理机制，导致计算机建模结果与实际地层分布情况差别较大，无法真实地反映缺失地层的空间展布特征。缺失地层引起的地质界面不连续会增加地层层面插值拟合的复杂度。虽然有研究者提出可以通过添加虚拟钻孔[7]或地质剖面[4,7]的方法将缺失地层界面控制信息追加到建模流程之中，但在具体实现的过程中，手工添加虚拟钻孔或地质剖面具有很大的主观性，同时也是一项极为繁琐的工作，不适合于用计算机进行自动或半自动的建模。

为解决这一难题，在综合前人成果的基础上，本文将对基于钻孔数据的沉积地层系统三维实体模型生成技术展开更为深入的研究。本文将首先总结归纳沉积地层系统的几何特征；然后基于多层DEM构模原理，提出一种新颖的三维地层模型生成技术“钻孔-层面-实体法”，给出具体的实现过程与关键算法；最后通过上海城建工程中的一个研究实例来验证该技术的有效性。

2 沉积地层系统的几何特征

沉积地层系统中的各个地层单元未经变形或轻微变形，没有被断层或节理切割，形态相对简单规则。按照地层的完整程度与空间分布特征，沉积地层系统中的地层可分为两类[6]：一类是完整地层，它在研究区内连续分布，其顶、底界面是完整的曲面；另一类是缺失地层，它在研究区内呈不连续分布，其顶、底界面分别由带有“空洞”的连续曲面组成，或是由多个不连续的曲面拼合而成。

根据不同的地质成因，本文将沉积地层系统中的缺失地层分为3类。第1类是由非沉积引起的缺失地层，即地层的缺失区域根本就没有发生过该地层的沉积，它一般是由地球内动力地质作用引起的。第2类是由侵蚀引起的缺失地层，即该地层沉积后，在上覆地层沉积前就遭受到了剥蚀，它一般是由地表外动力地质作用（如河流侵蚀、风化剥蚀）引起的。非沉积引起的缺失地层的缺失边界受控于下伏地层的顶面。侵蚀引起的缺失地层的缺失边界受控于上覆地层的底面。在实际的地层沉积过程中，还可能形成复合类别的缺失地层（本文称其为第3类缺失地层）。复合缺失地层的缺失边界既受控于上覆地层的底面，也受控于下伏地层的顶面。

基于大量的实例分析，可总结归纳出沉积地层系统所具备的5个几何特征：

①成层性。沉积地层系统可以按照一定的标准划分成若干个“层”，属于同一“层”的地质单元具有大体一致的沉积时代和物理力学指标，在某种程度上可以看作是同一类型的物质。

②顺序性。在给定的研究场区，可按照一定的标准和规则整理出一个标准的地层沉积顺序。

③连续性。沉积地层系统中的完整地层在研究区域内是连续分布的，缺失地层在局部区域会出现不连续，但可将缺失区域视为顶、底界面重合（零厚度）的连续地层进行特殊处理；因此，沉积地层系统中的所有地层都可视为连续层状地质体。

④封闭性。各个地层单元均由顶面、底面和侧面封闭而成，顶面和底面在水平面上的投影完全重合[8]；在三维建模时，只需要重构顶面和底面，侧面可自动生成。

⑤单值性。任一平面点P(x, y)在某一地层顶面或底面上对应的高程值惟一。

沉积地层系统三维建模的结果被称作三维地层模型，也常被称作“蛋糕”模型（“layer-cake”model）[1]。但实际的地层单元空间展布特征远比蛋糕中的分层复杂。由于缺失地层的存在，地层面与地层面之间会发生交切关系，进而导致地层在空间分布上的不连续，各个地层单元的几何形态趋于复杂。基于钻孔数据，快速构建地质合理、高精度的三维地层模型并不是一件容易的工作。在实际的三维地层构模算法设计与软件开发中，必须充分考虑并体现由缺失地层引起的地层尖灭、侵入、透镜体等特殊地质现象对三维地层模型的影响[8－10]。

3 构模原理

沉积地层系统的一个重要几何特征在于其各个地层及其控制界面按照一定的顺序有规律的堆叠在一起[1]。地层顶、底界面的重构是沉积地层系统三维模拟过程中最基础、最核心的工作。多层 DEM构模技术是近年来被广泛使用的构建沉积地层系统三维实体模型的方法，它具有输入数据简单、建模流程清晰、模型生成速度快、自动化程度较高等显著优点，目前已有多种实现算法，如地层层位法[4]、钻孔-层面模型法[5]和地层骨架构模法[2－3]。经过实践验证发现，地层层位法[4]和钻孔-层面模型法[5]仅适用于冲积环境下非沉积作用引起的缺失地层（第1类缺失地层），无法重构侵蚀作用引起的地层缺失。基于多层DEM构模技术改进的地层骨架构模法[3]考虑了河流侵蚀作用对地层的切割影响，在建模的过程中对地层层面进行了两次插值与高程调整，能够重构侵蚀作用引起的缺失地层（第2类缺失地层），但难以推广应用于第1类和第3类缺失地层。

现有的多层DEM实现算法对沉积顺序清晰、呈水平或近于水平的完整地层非常有效，但对地质构造活动强烈、包含多种缺失地层的复杂场区则建模效果较差，模型无法达到应有的精度，建模结果与实际情况出入较大。笔者认为，之所以会出现这种情况，主要是因为现有的构模算法没有全面考虑缺失地层形成的地质背景条件，无法将控制缺失地层空间展布特征的地质原理转化为计算机能够识别、编程的构模规则。针对这种缺陷，需要结合缺失地层形成的具体地质背景条件，对现有的构模算法进行优化、改进，以提高建模的精度与效率。

基于多层DEM构模原理，本文提出一种新颖的三维地层模型生成技术“钻孔-层面-实体法”。这种技术克服了先前技术方法的局限，既能构建非沉积引起的缺失地层，又能重构侵蚀引起的缺失地层，还能处理非沉积和侵蚀叠加形成的复合缺失地层，以及多个缺失地层组合在一起的情况。该技术的适应性强，准确性高，能够重构包含任意数目缺失地层的复杂沉积地层系统的精细三维实体模型。按照该技术构建三维地层模型共有11个关键环节。下面详细介绍建模过程中的各个具体步骤。

4 建模步骤

4.1 界定建模场区，提取相关钻孔信息

对于一个特定的研究场区，可能会有数目众多的钻孔。建模前，需要基于一个规范的数据库格式，将全部钻孔信息存储到关系数据库中。建模过程的第1步，就是从钻孔数据库中提取待建模场区的钻孔信息，包括钻孔类型、平面位置以及具体的地层分层信息。这些钻孔数据将作为后续的地层属性判别和地层顶、底界面插值拟合的初始数据。

4.2 建模场区总体地层编号与完整性判定

首先，将钻孔所揭示的地层按照沉积顺序进行编号，生成一个涵盖建模场区全部地层的“地层层序表”。进行地层编号的规则是“从老到新，逐层递增”，即：最老的地层编号为1，记为S1；其他地层按照沉积顺序（或形成时代）逐层加 1，递增编号，记为 S2、S3… Sn。

然后，根据钻孔对地层的揭示程度，将钻孔分为完全钻孔和不完全钻孔两类。将建模场区最新地层（即位于最顶部的地层）和最老地层（即位于最底部的地层）都探测到的钻孔为完全钻孔；否则为不完全钻孔。

接着，根据钻孔所揭示的地层信息，将建模场区的地层分为完整地层和缺失地层两类。在建模场区内，全部完全钻孔和可能探及此层的不完全钻孔都揭示到的地层为完整地层；否则为缺失地层。

需要指出的是，为了处理方便，本文假定整个建模场区的最顶层和最底层地层一定是完整地层。如果建模场区地层不满足这一条件，将在最顶层上方或最底层下方自动添加虚拟的完整地层，然后在完成“生成三维实体模型”（见第4.10节）操作后，自动剥除添加的虚拟地层。

4.3 钻孔数据离散化

钻孔分层信息是对上下相邻的地层的分界面的描述，能够揭示地层在钻孔位置处的竖向分布状况。建模过程的第3步，主要工作是将钻孔所揭示的地层分界面离散为三维空间中的一系列散点，并使用二分拓扑结构[6,9]来记录钻孔所蕴含的地层分层信息。在二分拓扑结构中，每一个散点均是两个地层的分界面上的控制点，使用该分界面的上层和下层地层编号来描述该散点的二分拓扑属性。每一个散点的数据结构如下：

经过钻孔数据离散化操作，可得到一个散点数据集P，集合了地层顶、底界面高程插值拟合的样本数据。另外，需要指出，不仅钻孔数据可离散为散点，其他可用的地质数据（如地质剖面图、地层等厚度线）都可离散化为三维空间中的散点，并使用二分拓扑结构来记录地层分层信息，然后添加到散点数据集P中作为地层控制界面插值拟合的样本点。

4.4 定义骨架三角网

沉积地层系统中各个地层的顶、底界面在水平面上的投影完全重合，因此，可定义一个骨架三角网作为拟合各个地层顶、底界面空间几何形态的基准三角网。所谓骨架三角网，是指以钻孔孔口平面坐标x、y为基准，在建模场区外边界的约束下，采用标准的三角化算法构网并细分加密的一个不规则三角网（TIN）[4－5]。骨架三角网不仅明确界定了待构建的三维地层模型的外边界，还隐式定义了各个地层顶、底界面上下严格一致的几何关系和拓扑关系。使用骨架三角网能减少后续的地层层面插值拟合、层面交切、高程调整、体元生成等处理步骤的复杂度，增强后续步骤实现算法的稳健性。

4.5 插值拟合地层顶、底界面

沉积地层系统中的每一个地层都由顶面三角网和底面三角网封闭而成（侧面可自动生成），这两个三角网都是基于骨架三角网生成的，因此，所有地层的顶、底界面都具有上下严格一致的几何关系和拓扑关系。在建模过程的第5步，从散点数据集P中提取各个地层顶、底界面的样本点坐标，利用这些散点插值拟合相应界面骨架三角网顶点的初始高程。

在拟合编号为 i的地层 Si的顶面三角网 Fi_Top时，从散点数据集P中提取m_ iBelowID为i的散点作为插值拟合的样本点；在拟合Si的底面三角网Fi_Bottom时，使用m_iAboveID为i的散点作为插值拟合的样本点。在进行插值时，可使用距离反比加权法、最邻近点法、自然邻近点法、径向基函数法、Kriging法等常用的插值算法。这些算法概念简单，方便快捷，既支持内插，又支持外推，实际应用效果良好。

4.6 判定缺失地层类别

这一步的工作是根据插值拟合出的缺失地层顶、底界面初始高程来自动推算缺失地层的类别。对于任一缺失地层Si，其顶面三角网记为Fi_Top，底面三角网记为Fi_Bottom。如果Si在钻孔Bj处缺失，则钻孔Bj被称作地层Si的缺失钻孔，缺失地层的上覆地层 Si+1与下伏地层 Si-1的分界点（简称为缺失点）记为 P0，P0的高程记为 Z0。Si的顶面三角网Fi_Top在钻孔 Bj处的顶点记为 PTop，底面三角网Fi_Bottom在钻孔Bj处的顶点记为PBottom。经过前一步插值拟合，可求得 PTop、PBottom的初始高程，分别记为 ZTop、ZBottom。使用式（1）计算 PTop、PBottom与P0之间的距离d1、d2：

由于 ZTop≥ZBottom，所以 d1≥d2。如果 d1=0、d2=0，即PTop、PBottom与缺失点P0重合，我们认为地层Si恰巧在钻孔Bj位置处尖灭，可作为0厚度的完整地层来对待；如果 d1≤0、d2＜0，则地层 Si在钻孔 Bj处非沉积缺失（图 1（a））。如果 d1＞0、d2≥0，则地层 Si在钻孔 Bj处侵蚀缺失（图 1（b））。如果d1＞0、d2＜0，则地层 Si在钻孔Bj处复合缺失（图1（c））。

除了地层Si恰巧在缺失钻孔位置处尖灭的情况之外，如果地层Si在全部缺失钻孔位置处均为非沉积缺失，认为该地层属于第1类缺失地层。如果地层Si在全部缺失钻孔位置处均为侵蚀缺失，则可认为该地层属于第2类缺失地层。如果地层Si在某些缺失钻孔位置处为复合缺失，或者在部分缺失钻孔位置处呈非沉积缺失、在部分缺失钻孔位置处侵蚀缺失，则认为该地层属于第3类缺失地层。

图1 根据地层顶、底界面初始高程判定缺失地层类别Fig.1 Determining the types of missing strata in terms of the initial elevations of the top and bottom surfaces

4.7 生成缺失地层处理次序

经过地层顶、底界面插值拟合生成了各地层顶、底界面三角网顶点的初始高程。对于完整地层，其顶面和底面三角网不会交叉，也不会与其他完整地层的顶、底界面三角网相交叉。但对于缺失地层，其顶面或底面三角网则可能会与其上覆地层或下伏地层的顶、底界面三角网交叉。需要根据缺失地层的类别，分别对缺失地层及其控制地层的顶、底界面进行交切处理与高程调整。

如果一个地层系统中存在多个缺失地层，在进行地层界面交切处理与高程调整前，需要按照地层的切错关系排出相应的优先级，生成缺失地层的处理次序。“钻孔-层面-实体法”按照下面的规则自动进行缺失地层排序工作：

①第3类缺失地层可视为第1类与第2类缺失地层叠加合成的结果。因此，在一个地层系统中，如果有第3类缺失地层，需要将第3类缺失地层分解为“第1类缺失地层+第2类缺失地层”，即将第3类缺失地层重复记录，它既属于第1类缺失地层，又属于第2类缺失地层。

②第1类缺失地层的优先级高于第2类缺失地层。在进行缺失地层交切处理与高程调整时，先处理第1类缺失地层，再处理第2类缺失地层。

③如果有多个第 1类缺失地层，按照“从老到新，逐个处理”的规则，先处理下层的缺失地层，再处理其上的缺失地层。

④如果有多个第 2类缺失地层，按照“从新到老，逐个处理”的规则，先处理上层的缺失地层，再处理其下的缺失地层。

经过排序，生成一个只含第1类缺失地层和第2类缺失地层的缺失地层处理队列。

4.8 缺失地层控制界面交切处理与高程调整

这一步的主要工作是按照前一步生成的缺失地层处理次序，逐个对缺失地层控制界面进行交切处理与高程调整。对于第1类和第2类缺失地层，因其受控于不同的地质界面，使用的处理方法也有差异，下面分别描述。

4.8.1 第1类缺失地层

如果地层Si属于第1类缺失地层，则Si的缺失边界受控于下伏地层Si-1的顶面。如图2（a）所示，经过4.5节的插值，拟合出Si的顶、底界面及其下伏地层 Si-1的顶面、上覆地层 Si+1的底面的初始形态。其中，Si的顶面三角网记为Fi_Top，底面三角网记为 Fi_Bottom，Si-1的顶面三角网记为 F(i-1)_Top，Si+1的底面三角网记为F(i+1)_Bottom。

首先，处理Si的顶面三角网Fi_Top。将Fi_Top与F(i-1)_Top进行相交运算，求出这两个三角网的所有交点，作为新顶点插入到骨架三角网中，同时修改Fi_Top、F(i-1)_Top以及其他全部地层顶、底界面三角网的顶点和拓扑关系。正常情况下，Fi_Top中顶点的高程应不低于F(i-1)_Top上对应的顶点。但在Si缺失的区域，会出现Fi_Top顶点的高程低于F(i-1)_Top上对应顶点的高程的情况。这时，需要逐个抬高 Fi_Top顶点的高程值，将其设定为与 F(i-1)_Top上对应顶点的高程值相等（如图 2（a）所示）。修改后的 Fi_Top记为F'i_Top。

然后，处理Si的底面三角网Fi_Bottom。从概念上来讲，Fi_Bottom与F(i-1)_Top的相应顶点高程理应完全一致。但由于Si是缺失地层，在4.5节分别插值求取这两个三角网顶点高程时，使用的样本点并不一致，这导致插值拟合出的对应顶点高程也不完全相同。这需要通过界面交切处理与高程调整来实现两个界面的一致。将Fi_Bottom与F(i-1)_Top进行相交运算，求出这两个三角网的所有交点，作为新顶点插入到骨架三角网中，同时修改 Fi_Bottom、F(i-1)_Top以及其他全部地层顶、底界面三角网的顶点和拓扑关系；接着，逐个比较Fi_Bottom与F(i-1)_Top的对应顶点高程是否相同：如果Fi_Bottom顶点的高程低于（或高于）F(i-1)_Top上对应顶点的高程，则抬高（或压低）Fi_Bottom顶点的高程值（如图 2（a）所示），将其设定为与F(i-1)_Top对应顶点的高程值相等。修改后的 Fi_Bottom记为 F’i_Bottom。

交切处理与高程调整后的缺失地层Si的顶、底界面如图2（b）所示。

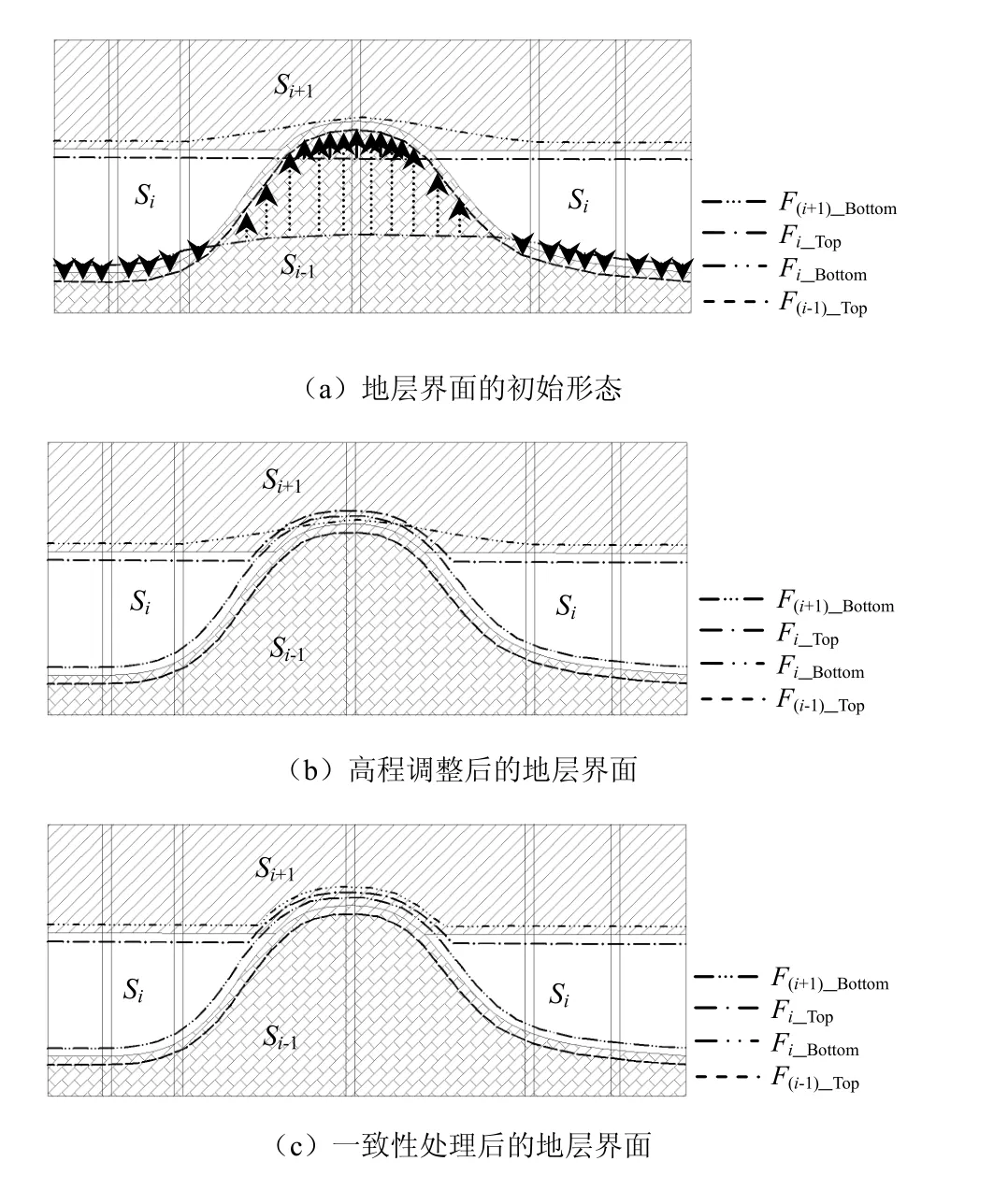
图2 第1类缺失地层控制界面交切处理、高程调整与一致性处理Fig.2 Intersecting surfaces, adjusting elevations and keep consistency for type 1 missing stratum

4.8.2 第2类缺失地层

如果地层Si属于第2类缺失地层，则Si的缺失边界受控于上覆地层Si+1的底面。如图3（a）所示，经过4.5节的插值，拟合出Si的顶、底界面及其下伏地层 Si-1的顶面、上覆地层 Si+1的底面的初始形态。其中，Si的顶面三角网记为Fi_Top，底面三角网记为 Fi_Bottom，Si-1的顶面三角网记为 F(i-1)_Top，Si+1的底面三角网记为F(i+1)_Bottom。

首先，处理Si的底面三角网Fi_Bottom。将Fi_Bottom与 F(i+1)_Bottom进行相交运算，求出这两个三角网的所有交点，作为新顶点插入到骨架三角网中，同时修改Fi_Bottom、F(i+1)_Bottom以及其他全部地层顶、底界面三角网的顶点和拓扑关系。正常情况下，Fi_Bottom中顶点的高程应不高于F(i+1)_Bottom上对应的顶点。但在Si缺失的区域，会出现Fi_Bottom顶点的高程高于 F(i+1)_Bottom上对应顶点的高程的情况。这时，需要逐个压低 Fi_Bottom顶点的高程值，将其设定为与F(i+1)_Bottom上对应顶点的高程值相等（如图3（a）所示）。修改后的Fi_Bottom记为F’i_Bottom。

然后，处理Si的顶面三角网Fi_Top。将Fi_Top与F(i+1)_Bottom进行相交运算，求出这两个三角网的所有交点，作为新顶点插入到骨架三角网中，同时修改Fi_Top、F(i+1)_Bottom以及其他全部地层顶、底界面三角网的顶点和拓扑关系；接着，逐个比较 Fi_Top与F(i+1)_Bottom的顶点高程是否相同：如果Fi_Top顶点的高程低于（或高于）F(i+1)_Bottom上对应顶点的高程，则抬高（或压低）Fi_Top顶点的高程值（如图3（a）所示），将其设定为与F(i+1)_Bottom对应顶点的高程值相等。修改后的Fi_Top记为F'i_Top。

交切处理与高程调整后的地层Si的顶、底界面如图3（b）所示。

4.9 缺失地层与邻接地层界面一致性处理

这一步的主要工作是按照4.7节生成的缺失地层处理次序，逐个处理缺失地层与邻接地层的公共界面，以保证上下邻接地层公共界面的一致性，即：所有地层（无论是完整地层，还是缺失地层）的顶面三角网与其上覆地层的底面三角网完全一致，所有地层的底面三角网与其下伏地层的顶面三角网完全一致。

如果地层Si属于第1类缺失地层，则逐个修改上覆地层 Si+1底面三角网 F(i+1)_Bottom的顶点高程，使其与 F'i_Top完全相同。修改后的 F(i+1)_Bottom记为F'(i+1)_Bottom。如果地层Si属于第2类缺失地层，则逐个修改下伏地层Si-1顶面三角网F(i-1)_Top的顶点高程，使其与 F'i_Bottom完全相同。修改后的 F(i-1)_Top记为 F'(i-1)_Top。一致性处理后的地层顶、底界面分别如图2（c）（第1类缺失地层）、图3（c）（第2类缺失地层）所示。

图3 第2类缺失地层控制界面交切处理、高程调整与一致性处理Fig.3 Intersecting surfaces, adjusting elevations and keep consistency for type 2 missing stratum

4.10 生成三维实体模型

经过前面各步的处理，完成了各个地层顶、底界面三角网的重构工作，生成了由三角面片组成的地层顶、底界面。这一步的工作是：从下到上逐个处理各个地层，以其顶面三角网和底面三角网为空间基准，挤压各个地层顶面三角网和底面三角网[4]，形成块体模型；也可使用三维空间离散化技术对顶面三角网和底面三角网围成的空间进行剖分，生成用三棱柱体元充填的三维实体模型。

4.11 三维可视化分析

最后，对生成的地层实体模型进行常规的可视化展示与专业的三维分析，包括三维观察、交互定位、模型剖切、隧洞开挖、体积量算等。基于三棱柱体元表示的三维实体模型非常适合于空间查询与空间分析，能够直观、准确、全面地展示三维地层模型的内部信息。

5 研究实例

研究场区位于上海市普陀区苏州河畔，面积约800 m×600 m。如图4（a）所示，研究区内6个钻孔揭示了4个地层（从下到上依次简记为S1～S4），其中地层S1、S4是完整地层，S2、S3是缺失地层。图4（b）～4（f）是使用这6个钻孔数据自动生成的各地层的控制界面以及三维实体模型。其中，图4（b）展示了地层分界面的空间分布，图4（c）、4（d）是从不同视角查看的三维实体模型，图4（e）是过钻孔C2、C6、C5、C4生成的剖面，图4（f）是对三维实体模型进行剖切操作后生成的栅状图。

从图4中可以看出：地层S2、S3在某些钻孔位置处（如C2）为非沉积缺失，在某些钻孔位置处（如C4）为侵蚀缺失，地层的顶、底界面受非沉积作用和侵蚀作用共同控制，因此，属第3类缺失地层；使用“钻孔-层面-实体法”自动重构出来的地层顶、底界面形态自然，缺失地层的控制边界也很合理。为了定量评估这个模型的精度，笔者使用实际工程建设过程中新增的钻孔和基坑开挖数据进行模型检验。结果发现，在本文所构建的三维地层模型中，完整地层顶、底界面高程与实测数据的误差在5 cm以内，缺失地层顶、底界面高程与实测数据的误差小于8 cm。总体来看，模型的精度较高，可直接应用于工程实际。这个实例直观地展示了“钻孔-层面-实体法”处理复合缺失地层的有效性和合理性，说明其具有自动重构复杂地质条件下形成的沉积地层系统的能力。

图4 复合缺失地层构模实例Fig.4 Example of missing strata induced by combined action

6 结 语

沉积地层系统三维重构的难点主要体现在对缺失地层地质成因的判定以及缺失边界的界定上。本文提出的“钻孔-层面-实体法”克服了先前技术方法的局限，能充分挖掘钻孔数据所揭示、隐含的地质背景信息，自动判断缺失地层的地质成因并界定缺失边界，真实地反映缺失地层及其控制界面的空间展布特征与实际交切关系。与先前的技术方法相比，“钻孔-层面-实体法”具有算法稳健、自动性高、建模结果合理、模型精度高等显著优势。另外，“钻孔-层面-实体法”在实现的过程中，巧妙地将控制地层空间几何形态的地质原理转化为计算机能够识别、编程的构模规则，这对进一步研究复杂地质体三维构模技术具有重要的借鉴意义。

[1]TURNER A K. Challenges and trends for geological modelling and visualization[J]. Bulletin of Engineering Geology and the Environment, 2006, 65(2): 109－127.

[2]贺怀建, 白世伟, 赵新华, 等. 三维地层模型中地层划分的探讨[J]. 岩土力学, 2002, 23(5): 637－639.HE Huai-jian, BAI Shi-wei, ZHAO Xin-hua, et al.Discussion on strata partition in three-dimension strata model[J]. Rock and Soil Mechanics, 2002, 23(5): 637－639.

[3]朱良峰, 潘信. 河流侵淤作用下三维地层模型的构建[J].岩土力学, 2005, 26(增刊1): 65－68.ZHU Liang-feng, PAN Xin. Reconstruction of 3D stratigraphic model for fluvial erosion and aggrading action[J]. Rock and Soil Mechanics, 2005, 26(Supp.1):65－68.

[4]LEMON A M, JONES N L. Building solid models from boreholes and user-defined cross-sections[J]. Computers& Geosciences, 2003, 29(5): 547－555.

[5]朱良峰, 吴信才, 刘修国, 等. 基于钻孔数据的三维地层模型的构建[J]. 地理与地理信息科学, 2004, 20(3):26－30.ZHU Liang-feng, WU Xin-cai, LIU Xiu-guo, et al.Reconstruction of 3D strata model based on borehole data[J]. Geography and Geo-Information Science, 2004,20(3): 26－30.

[6]张芳, 朱合华, 宁民霞. 适于海量数据的三维地层建模方法[J]. 岩石力学与工程学报, 2006, 25(增刊1): 3305－3310.ZHANG Fang, ZHU He-hua, NING Min-xia. Modeling method of 3D strata suitable for massive data[J]. Chinese Journal of Rock Mechanics and Engineering, 2006,25(Supp.1): 3305－3310.

[7]朱良峰, 吴信才, 潘信. 三维地层模型误差修正机制及其实现技术[J]. 岩土力学, 2006, 27(2): 268－271.ZHU Liang-feng, WU Xin-cai, PAN Xin. Mechanism and implementation of error correction for 3D strata model[J].Rock and Soil Mechanics, 2006, 27(2): 268－271.

[8]徐能雄, 何满潮. 层状岩体三维构模方法与空间数据模型[J]. 中国矿业大学学报, 2004, 33(1): 103－108.XU Neng-xiong, HE Man-chao. 3D modeling methods and spatial data model of layered rock-mass[J]. Journal of China University of Mining & Technology, 2004,33(1): 103－108.

[9]朱合华, 吴江斌. 基于Delaunay构网的地层2D，2.5D建模[J]. 岩石力学与工程学报, 2005, 24(22): 4073－4079.ZHU He-hua, WU Jiang-bin. 2D and 2.5D modeling of strata based on Delaunay triangulation[J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24(22): 4073－4079.

[10]赵宏坚, 周翠英. 基于实体建模的三维地层构造[J]. 岩土力学, 2010, 31(4): 1257－1263.ZHAO Hong-jian, ZHOU Cui-ying. Solid-oriented 3D-stratum construction[J]. Rock and Soil Mechanics,2010, 31(4): 1257－1263.