锚杆长度和间距对洞室抗爆性能影响研究

徐景茂 ，顾金才，陈安敏，张向阳，明治清

（1. 中国科学技术大学 近代力学系，合肥 230027；2. 总参工程兵科研三所，河南 洛阳 471023）

1 引 言

锚杆加固作为一种有效的、主动的岩体加固方式[1－3]，被广泛应用于民用工程和国防工程中，如地下厂房、煤矿巷道、地下机库、导弹发射井等，众多学者通过大量的研究，已基本弄清了锚杆在静载作用下的加固机制和设计计算方法[4－6]，但随着现代精确制导钻地武器的发展[7－9]，地下锚固洞室将受到爆炸荷载的威胁，然而锚杆的动态力学性能特别是其对围岩的抗爆加固效果等方面的研究却相对较少。Tannant等[10]通过现场试验，研究了端头锚固锚杆在爆炸载荷作用下的动力特性，测量了锚杆的动态应变和岩体表面质点速度，指出爆炸荷载对锚杆预应力的影响主要有爆炸脉冲振幅、持续作用时间和荷载循环3个因素。Ortlepp等[11]研究了静载和动载条件下大变形坑道的加固形式，指出屈服锚杆可以吸收大量能量而使坑道不发生破坏。杨苏杭等[12]用模型试验研究了爆炸过程中锚杆预应力的变化情况。易长平等[13]通过理论分析，研究了爆破振动对砂浆锚杆的影响。Zhang等[14]、薛亚东等[15]、荣耀等[16]分别利用数值模拟，研究了锚杆在应力波作用下的力学响应。杨湖等[17]通过理论分析研究了波在锚杆体内波动能量的外泄特征以及弹性波在锚杆、岩土介质及其耦合体系中的传播规律，得到了波在锚固体系中的衰减规律及传播机制。

本文根据Froude相似理论，通过集中装药下的模型试验，对普通锚杆、中密锚杆、长密锚杆、短密锚杆及长短相间密锚杆加固洞室的抗爆性能进行了研究，分析了不同长度、间距的全长粘结式锚杆加固洞室在围岩应力、洞壁加速度、洞室拱顶底板相对位移、洞壁环向应变、洞室破坏形态等方面的不同特点。本文还采用FLAC3D对模型试验进行了模拟，并利用参数化建模方法分析了洞顶位移随锚杆长度间距的变化规律。

2 模型试验研究

2.1 相似理论

目前模型试验中广泛采用的两种相似理论为复制相似理论和Froude相似理论。两种相似理论的比例系数见表1。

表1 相似比例系数Table 1 Similar scale factors

复制相似理论中试验模型通常由与原型一样的材料构成，其比例定律表明，加速度比例系数应该是长度比例系数的倒数，这一要求可用离心机来满足；Froude相似理论中基本变量由长度、质量密度和加速度组成，加速度被选作基本变量并且指定它的比例系数为单位 1，因而不需要采用离心机进行试验，但其比例定律表明，原型材料不能用来制作小比尺模型，而应该用相似材料代替原型材料，它要求应力比例系数与密度比例系数和几何比例系数之间满足关系：=，因为密度比例系数与几何比例系数的乘积通常小于 1，所以相似材料必须比原型材料更软。本次模型试验根据Froude相似理论，采用相似材料来开展。

2.2 模型设计

试验原型洞室为直墙拱顶型，跨度为5 m，Ⅲ类围岩，完全埋置爆炸TNT当量500 kg。

Ⅲ类围岩采用低标号水泥砂浆模拟，其力学参数如表2。

表2 模型介质材料力学参数Table 2 Mechanical parameters of model material

模型洞室跨度D为60 cm，相似比例系数可确定为：几何比例系数= 0.12，密度比例系数=0.70，应力比例系数= 0.084。φ25 mm的螺纹钢筋锚杆采用φ1.84 mm的铝棒模拟，近似满足抗拉变形刚度相似。模型中锚杆孔直径为 6 mm，注浆材料采用石膏浆模拟，其力学参数如表3所示。

表3 石膏浆材料力学参数Table 3 Mechanical parameters of gypsum grout

试验中装药量按爆炸应力波峰值相似来确定，根据1986年美国陆军部修定出版的《常规武器防护设计原理》[18]中介绍，爆炸应力波峰值计算公式为

式中：P为应力波峰值；ρ为介质密度；C为应力波波速；f为耦合系数；n为衰减系数；为比例距离，为所求点至爆心距离，W为装药量。根据相似理论，装药量的立方根相似比例系数为

模型试验在总参工程兵科研三所“岩土工程抗爆结构模型试验装置”[19]上进行，每块模型尺寸均为长×宽×高=240 cm×150 cm×230 cm。沿着模型的长度方向开挖直墙拱顶型毛洞，其跨度为60 cm，直墙高25 cm，拱高17 cm，圆拱半径35 cm。为了尽可能地创造相同的对比试验条件和减少试验工作量，将每个毛洞分为两个试验段，每段长120 cm，在试验段的中间部位采用不同类型的锚杆对毛洞进行加固，加固长度为60 cm，加固范围以外仍为毛洞，从而形成两个加固试验段，加固试验段之间用一宽1 cm、深5 cm的槽隔开，以保证各加固形式的边界条件相同。各加固洞室参数如表4和图1所示。爆心在各加固段中部正上方，每个加固段进行3次爆炸试验，爆心距洞室拱顶的距离 R分别为83、63、48 cm，装药对应的埋深He分别为50、70、85 cm，洞室埋深H =R +He =133 cm保持不变。试验时在爆心正下方围岩中布置了垂直应力测点，在洞室拱顶和底板布置了加速度测点，在洞室拱顶和底板之间布置了相对位移测点，在洞壁环向布置了应变测点，如图2所示。试验完成后对模型进行解剖，分析洞室破坏形态。

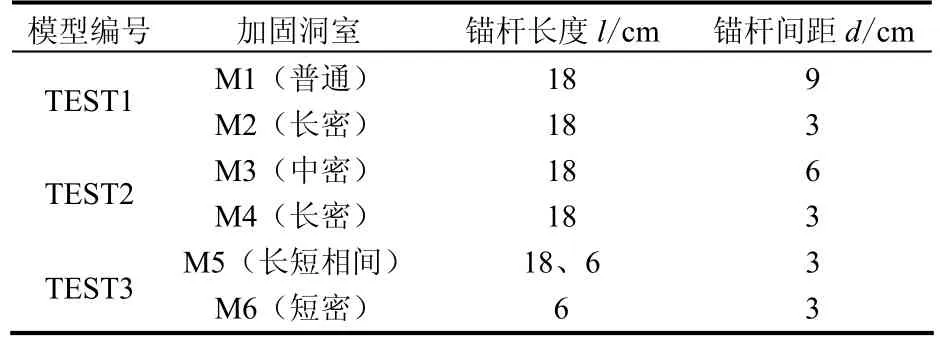
表4 模型试验概况Table 4 Survey of model tests

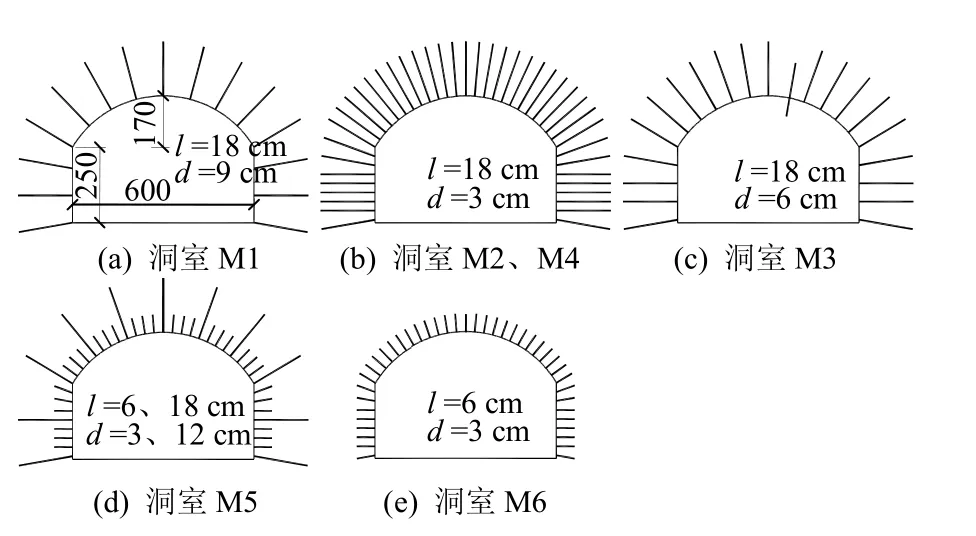
图1 各洞室加固型式（单位：mm）Fig.1 Reinforcement patterns of different tunnels (unit: mm)

图2 测点布置（单位：mm）Fig.2 Arrangement plans of measuring points (unit: mm)

2.3 试验结果分析

2.3.1 围岩应力分析

以第2炮（R=63 cm）为例，爆心正下方洞室拱顶正上方围岩垂直应力峰值P实测结果如图3所示，图中r为测点至拱顶的距离，Rc为模型介质抗压强度，R/W1/3为比例爆距（m/kg1/3）。比较 M1、M2、M3可以看出，锚杆长度相同时，随锚杆间距的减小，围岩垂直应力峰值略有增大（M1＜M3＜M2）；比较 M4、M5、M6可以看出，锚杆间距相同时，随锚杆长度的增加及长锚杆数量的增多，围岩垂直应力峰值也略大（M6＜M5＜M4）。这是因为间距小、长度大的锚杆加固的围岩整体等效密度和等效弹性模量都略大，从而等效波阻抗也较大，而波阻抗是为使介质产生单位质点速度增量所需要加给介质的扰动应力增量，所以应力峰值也必然有所增加。

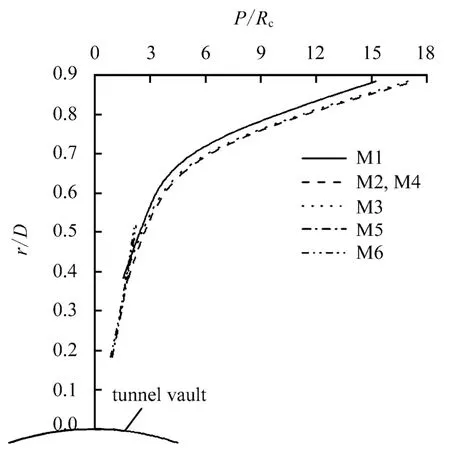
图3 围岩垂直应力峰值实测结果（R/W1/3 =1.357 3 m/kg1/3）Fig.3 Measured results of vertical stress peak values

2.3.2 洞壁加速度分析

图4为不同比例距离下洞壁加速度峰值的变化情况。

比较 M1、M2、M3可以看出，锚杆长度相同时，随锚杆间距的减小，拱顶加速度峰值明显减小（M1＞M3＞M2），而底板加速度峰值则明显增加（M1＜M3＜M2），如 M2拱顶加速度峰值比 M1小29%～40%，M2底板加速度峰值比M1大2～7倍。比较 M2（M4）、M5、M6可以看出，锚杆间距相同时，随锚杆长度的增加及长锚杆数量的增多，拱顶加速度峰值明显减小（M6＞M5＞M2），而底板加速度峰值则明显增加（M6＜M5＜M2），如 M2拱顶加速度峰值比M6小25%～29%，M2底板加速度峰值比M6大1～2倍。从图4(b)还可看出，当锚杆间距减小、锚杆长度增加及长锚杆数量增多时，底板加速度峰值随比例距离减小而增加的速度也更快。其原因是小间距的密锚杆加固围岩的整体性较好，长锚杆加固围岩的范围较大，在洞室上方形成的高强拱圈能承受更大的荷载，并将荷载通过围岩的整体性传至侧墙及底板，从而使底板加速度峰值随比例距离减小而迅速增大；相对而言，大间距锚杆加固围岩的整体性较差，短锚杆加固围岩的范围较小，使得洞室上方加固区以外的围岩容易破坏，并产生卸荷作用，导致传至底板的荷载相对较小，底板加速度峰值增速相对不明显。

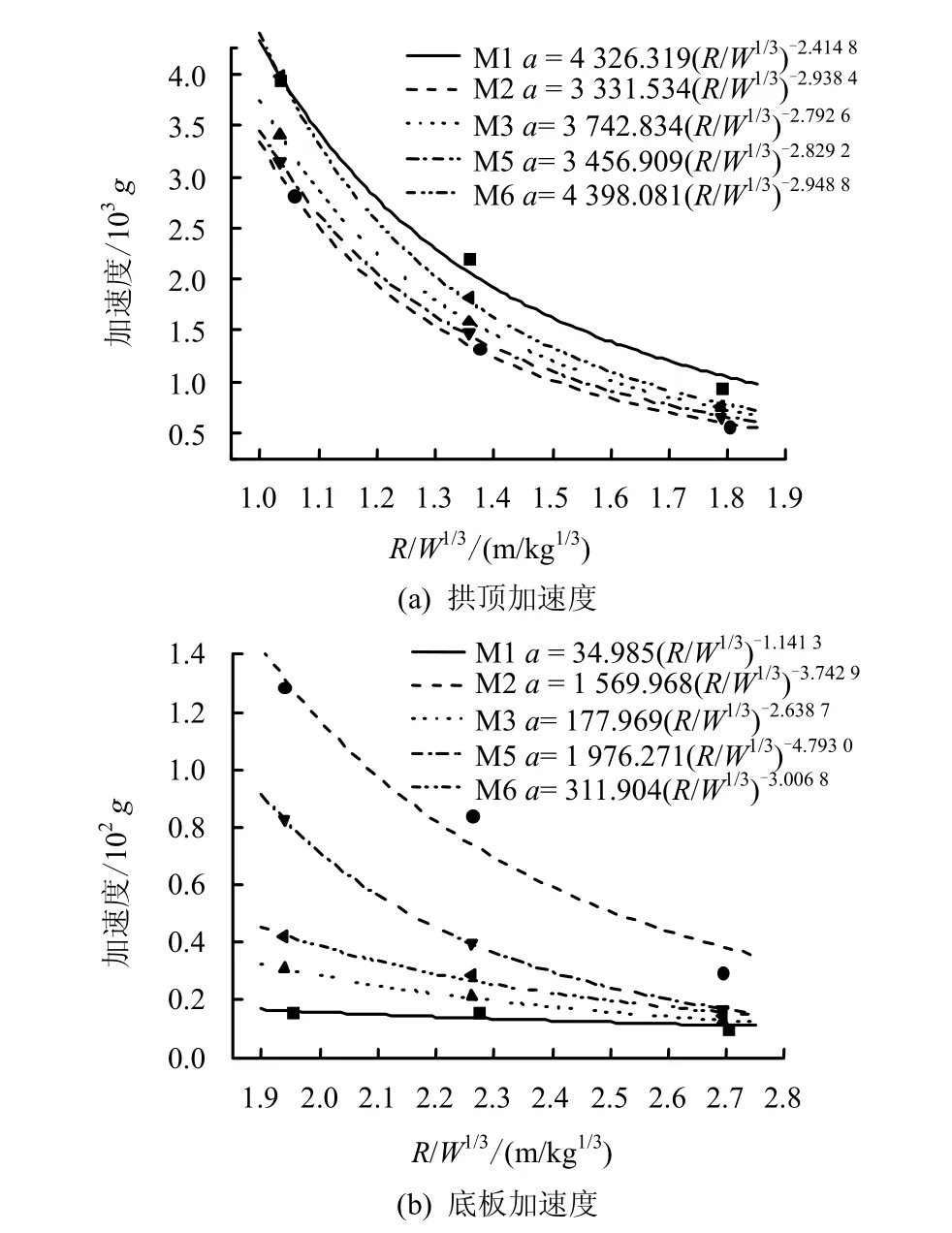
图4 加速度峰值与比例距离关系曲线Fig.4 Relation curves between acceleration peak value and scaled distance

2.3.3 洞壁位移分析

图5为不同比例距离下拱顶底板相对位移峰值及残余值的变化情况。

从图中可看出，在锚杆长度相同时，无论是位移峰值还是位移残余值，均随锚杆间距的减小而大幅度减小（M1＞M3＞M2），如 M2位移峰值和残余值分别比M1小63%～81%和65%～86%。在锚杆间距相同时，随锚杆长度的增加及长锚杆数量的增多，位移峰值和残余值也有一定程度的减小（M6＞M5＞M2），如 M2位移峰值和残余值分别比M6小42%～67%和19%～69%。

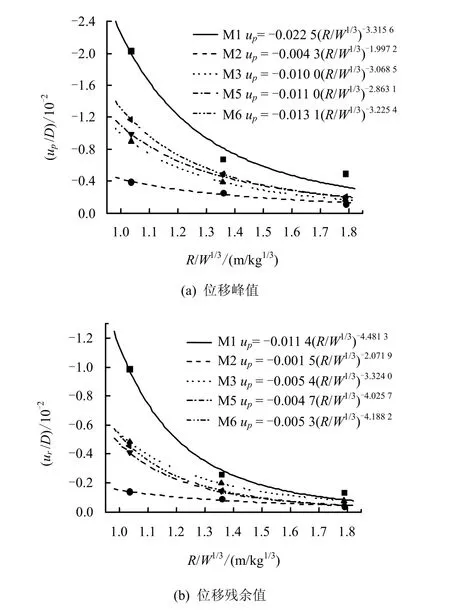
图5 拱顶底板相对位移与比例距离关系曲线Fig.5 Relation curves between vault-footwall displacement and scaled distance

2.3.4 洞壁应变分析

图6为第2炮（R =63 cm）时洞壁环向应变峰值和残余值的分布。从图中可看出，在锚杆长度相同时，拱脚压应变峰值和残余值均随锚杆间距的减小而明显减小（M1＞M3＞M2），如 M2拱脚压应变峰值比M1约小31%，残余值比M1约小46%；在锚杆间距相同时，比较 M2、M5、M6可知，长锚杆虽能减小拱脚压应变峰值和残余值，但并不如锚杆间距那样明显，而且使得拱顶拉应变峰值明显增大（M5＞M2＞M6），局部增长锚杆时尤为严重，如M5，约为M6拱顶拉应变峰值的4.5倍。

2.3.5 围岩破坏形态分析

图7为各洞室围岩破坏形态。如图 7(a)，M1洞室拱部发生严重变形，已经不再是弧形，且拱顶上方发生倒漏斗状大面积松动，松动范围宽为42 cm、高为20 cm，高度已超出锚杆加固区域。如图7(c)，在M3洞室拱部两侧拱脚上方介质内产生一条或多条斜向剪切裂缝，裂缝由爆心向下成喇叭口状，有的裂缝直接穿过锚杆，有的裂缝发生在锚固区锚杆外端，这说明较稀的锚杆支护不能阻止围岩裂缝进入锚固区，裂缝可以跨过锚杆发展。

图6 洞壁环向应变分布（R/W1/3 =1.357 3 m/kg1/3）Fig.6 Distributions of circumferential strain of tunnel wall

图7 围岩破坏形态Fig.7 Failure modes of surrounding rock

如图7(b)，M2洞室与M3洞室相比，虽然二者均在洞室拱脚部位产生多条斜向裂缝，但M2洞室围岩裂缝均发生在锚杆长度范围之外，锚杆内部未见裂缝，这说明加大锚杆密度可以阻止裂缝的穿入。如图7(e)，M6也是在洞室拱部两侧拱脚部位产生一条或多条斜向裂缝，并且裂缝也是只发生在锚杆长度之外，没有穿入锚固区内，但裂缝部位与长密锚杆支护洞室M2相比更靠近洞壁，因而危险程度也相应较大。如图7(d)，M5与M6相比，在短密锚杆支护的基础上，相间增加了几根长锚杆，就阻止围岩裂缝的产生与发展来说，没有起明显作用，围岩裂缝毫无改变地穿过了长锚杆。

3 数值模拟分析

3.1 计算模型

采用FLAC3D对模型试验进行模拟，材料模型采用Mohr-Coulomb弹塑性本构模型。FLAC3D程序中缺少模拟炸药爆炸的药包单元，爆炸荷载动力源需要人工输入。试验中实测100 g TNT集团装药形成的爆腔半径为15 cm左右，根据实测压力波形及其衰减规律的分析，得到爆腔处的压力曲线如图 8所示。

图8 爆腔处压力曲线Fig.8 Pressure curves at explosion cavity

将上述拟合曲线施加到FLAC3D模型体内与模型试验爆点深度一样、半径一样的球腔（爆腔）内壁上，如图9所示，即可模拟爆炸荷载。

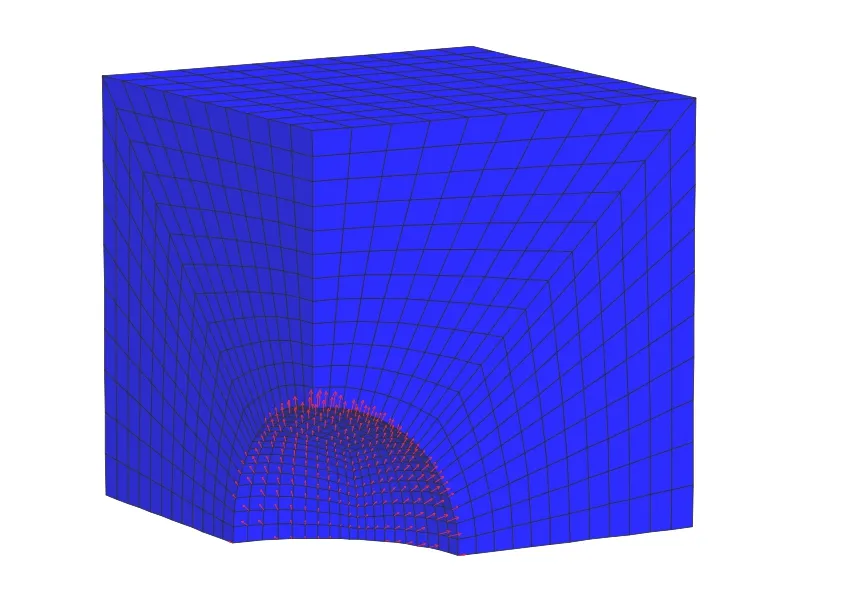
图9 爆腔处施加的动压力荷载Fig.9 Applied dynamical pressure at explosion cavity

根据试验模型的对称性取1/4模型进行建模，爆腔附近和洞室周围网格划分较细，其他部分网格较疏，这样既可以保证计算的精度，又不至于造成计算时间的浪费。为了避免应力波传至边界产生反射波，从而影响计算结果，在模型中引入了非反射边界条件，本次计算采用软件自带的静态黏滞边界。实际岩体的阻尼效应是非常明显的，它使得爆炸能量散逸而耗损，计算中采用了常用的瑞利阻尼。另外，为了比较不同长度、间距锚杆加固洞室的抗爆性能，建模时采用了Fish语言，对48种不同长度、间距的锚杆支护方案进行了模拟。限于篇幅，这里只对计算位移进行分析。

3.2 计算位移与实测位移的比较

图10为第1炮（R=83 cm）时各加固洞室在t =10 ms时的计算位移云图，可以看到未加固洞室M0的拱顶位移集中现象最明显，其次是M1、M6、M3，而M2、M5的拱部位移趋于均匀化，这是因为M2、M5加固方案形成的加固围岩拱效应相对明显，拱部围岩的密度、刚度、波阻抗在更大范围内得到较大的提高，应力波在拱部围岩中的传播速度也相应增大，从而使得爆炸荷载迅速转移至侧墙外围（如图10(c)、10(e)），减小了拱部荷载的集中程度。

图11为第2炮（R =63 cm）时各加固洞室拱顶位移计算波形与实测波形，为了便于比较，各图中增加了未加固洞室M0的计算值。从图中可以看到：①计算波形和实测波形的形状基本相似，都是先向下到达负峰值后再反弹，实测波形的反弹幅度较大；②计算峰值略小于实测峰值，计算残余值大于实测残余值；③计算波形的上升时间较短，但作用时间与实测波形相差不大；④普通锚杆（M1）减小洞室拱顶位移的效果不明显，而长密锚杆（M2、M4）减小洞室拱顶位移的效果显著。

可见，计算位移与实测位移一致性较好，能够正确反映出各加固洞室抗爆性能的差异。

3.3 位移随锚杆间距长度的变化规律

通过参数化设计计算方法改变锚杆间距和长度，分析了间距d为1.5、3、4.5、6、7.5、9 cm和长度l为3、6、9、12、15、18、21、24 cm相互组合的48种加固洞室的抗爆效果，得到第1炮（R=83 cm）时洞室拱顶位移随锚杆间距长度的变化规律，如图12所示。

（1）当锚杆长度很小时，锚杆间距的变化对洞室拱顶位移的影响甚微，密锚杆也无法发挥作用，锚杆长度不宜小于洞室跨度的1/10。

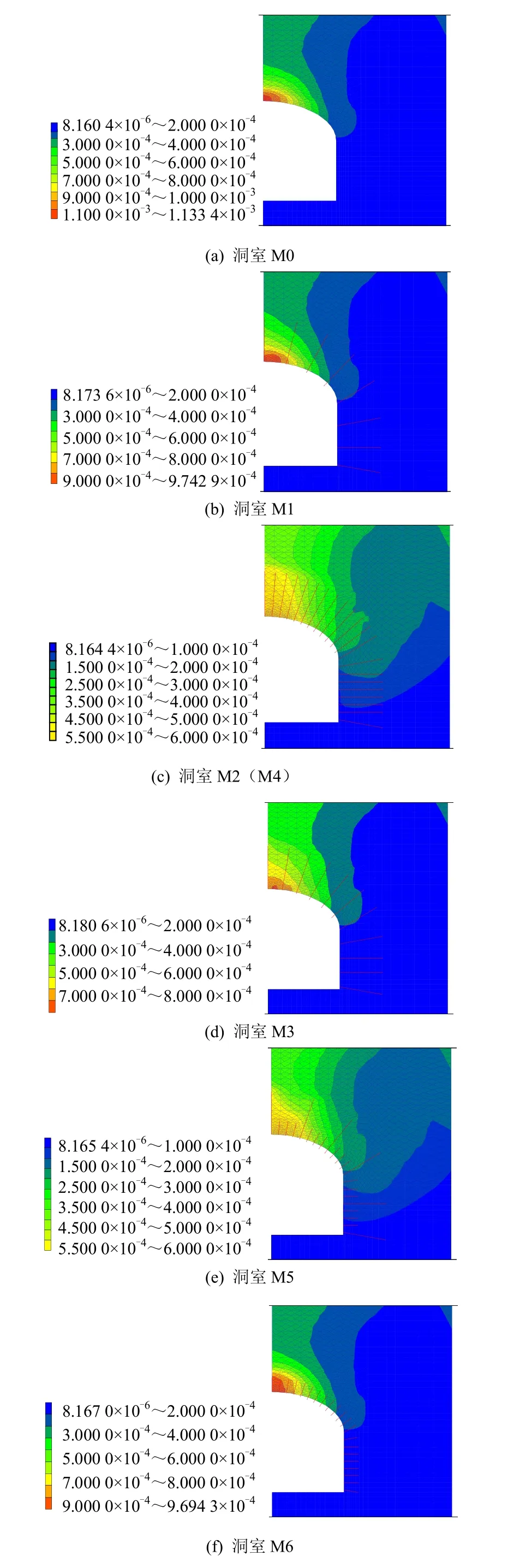
图10 计算位移云图（R/W1/3 =1.788 2 m/kg1/3）Fig.10 Nephograms of calculated displacement

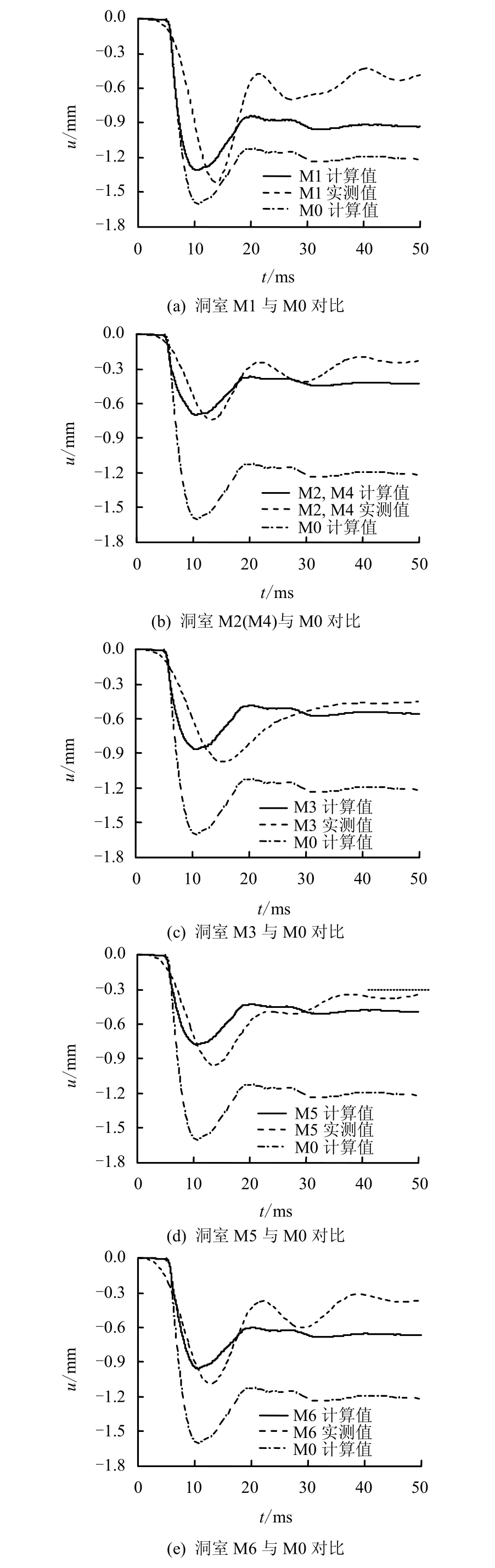
图11 计算位移与实测位移比较图(R/W1/3=1.357 3 m/kg1/3)Fig.11 Comparisons between calculated displacement and measured displacement

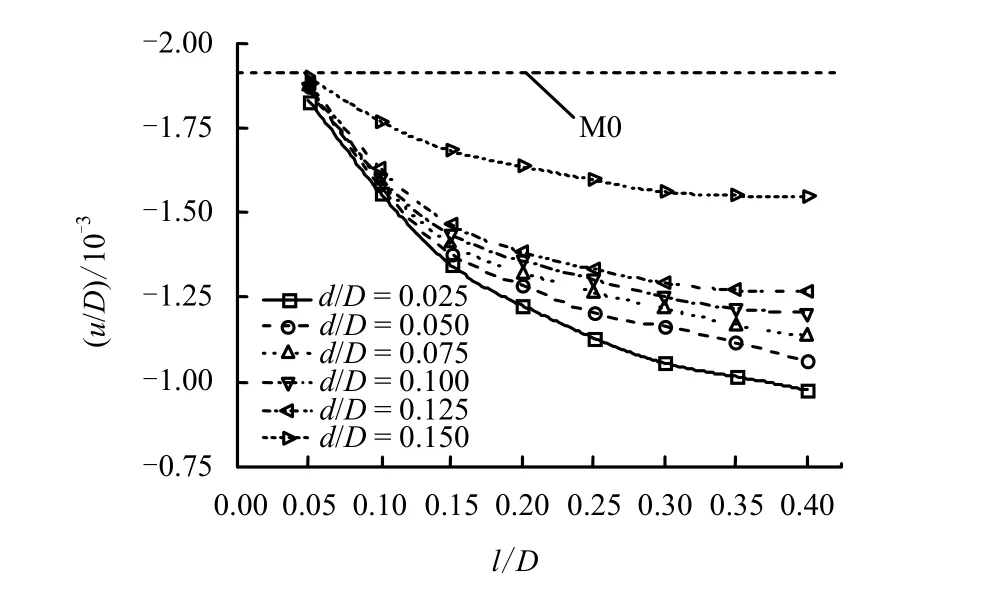
图12 洞室拱顶位移随锚杆间距和长度的变化规律Fig.12 Variation regularity of vault displacement with the change of anchor length and spacing

（2）在锚杆间距一定的情况下，洞室拱顶位移随锚杆长度的增加而减小，但当锚杆长度增加到一定程度后，位移减小的效果并不明显，锚杆的最佳长度约为0.35倍的洞室跨度，可取为1/3洞室跨度。

（3）在锚杆长度一定的情况下，洞室拱顶位移随锚杆间距的减小而减小。

（4）当锚杆间距较大时，锚杆对洞室拱顶位移的减小效果不明显，只有当锚杆间距不大于洞室跨度的1/8时，锚杆才会发挥有效作用。

（5）从减小洞室拱顶位移的效果来看，减小锚杆间距比增加锚杆长度更有效，但从经济实用角度来考虑，锚杆间距不宜过小，否则造成浪费，且给施工带来困难，如本次模型试验中锚杆间距为3 cm（D/20），对应实际工程中锚杆间距仅为 3/0.12=25 cm，施工不便。因此，本文建议锚杆的最佳间距为1/15洞室跨度，即模型中为4 cm，对应原型为33 cm，根据文献[20]，该间距的锚杆施工是可行的。

4 结 论

（1）减小锚杆间距比增加锚杆长度更能有效地提高洞室抗爆能力，且锚杆间距必须达到一定密度时才可以阻止围岩裂缝进入锚固区。

（2）在锚杆长度相同的情况下，密锚杆能明显减小洞室拱顶加速度峰值、拱顶底板相对位移峰值、残余值和拱脚部位压应变峰值、残余值。

（3）当锚杆长度增加到一定程度后，加固的效果并不明显，而且带来了底板加速度峰值、拱顶拉应变峰值的增加。

（4）锚杆的最佳长度可取为1/3洞室跨度，锚杆的最佳间距可取为1/15洞室跨度。

[1]（英）T. H汉纳著.锚固技术在岩土工程中的应用[M].胡定, 邱作中, 刘浩吾译. 北京: 中国建筑工业出版社,1987.

[2]程良奎. 岩土锚固的现状与发展[J]. 土木工程学报,2001, 34(3): 7－12.CHENG Liang-kui. Present status and development of ground anchorages[J]. China Civil Engineering Journal,2001, 34 (3): 7－12.

[3]顾金才, 陈安敏. 岩体加固技术研究之展望[J]. 隧道建设, 2004, 24(1): 1－2, 5.GU Jin-cai, CHEN An-min. Prospect of rock reinforcement technique research[J]. Tunnel Construction, 2004, 24(1): 1－2, 5.

[4]中国岩石力学与工程学会岩石锚固与注浆委员会. 锚固与注浆技术手册[S]. 北京: 中国电力出版社, 1999.

[5]赵长海. 预应力锚固技术[M]. 北京: 中国水利水电出版社, 2001.

[6]闫莫明, 徐祯祥, 苏自约. 岩土锚固技术手册[M]. 北京: 人民交通出版社, 2004.

[7]金丰年, 刘黎, 张丽萍, 等. 深钻地武器的发展及其侵彻[J]. 解放军理工大学学报（自然科学版）, 2002, 3(2):34－40.JIN Feng-nian, LIU Li, ZHANG Li-ping, et al.Development of projectiles and their penetration[J].Journal of PLA University of Science and Technology(Natural Science), 2002, 3(2): 34－40.

[8]王涛, 余文力, 王少龙, 等. 国外钻地武器的现状与发展趋势[J]. 导弹与航天运载技术, 2005, (5): 51－56.WANG Tao, YU Wen-li, WANG Shao-long, et al. Present status and tendency of foreign earth-penetrating weapons[J]. Missiles and Space Vehicles, 2005, (5): 51－56.

[9]吴静, 邓堃, 柳世考. 美军精确制导武器及其对抗技术的分析[J]. 飞航导弹, 2007, 6: 12－16.

[10]TANNANT D D, BRUMMER R K, YI X. Rockbolt behaviour under dynamic loading: Field tests and modelling[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1995, 32(6): 537－550.

[11]ORTLEPP W D, STACEY T R. Performance of tunnel support under large deformation, static and dynamic loading[J]. Tunnelling and Underground Space Technology, 1998, 13(1): 15－21.

[12]杨苏杭, 梁斌, 顾金才, 等. 锚固洞室抗爆模型试验锚索预应力变化特性研究[J]. 岩石力学与工程学报, 2006,25(增刊 2): 3750－3756.YANG Su-hang, LIANG Bin, GU Jin-cai, et al. Research on characteristics of prestress change of anchorage cable in anti-explosion model test of anchored cavern[J].Chinese Journal of Rock Mechanics and Engineering,2006, 25(Supp. 2): 3750－3756.

[13]易长平, 卢文波. 爆破振动对砂浆锚杆的影响研究[J].岩土力学, 2006, 27(8): 1312－1316.YI Chang-ping, LU Wen-bo. Research on influence of blasting vibration on grouted rockbolt[J]. Rock and Soil Mechanics, 2006, 27(8): 1312－1316.

[14]ZHANG C S, ZOU D H, MADENGA V. Numerical simulation of wave propagation in grouted rock bolts and the effects of mesh density and wave frequency[J].International Journal of Rock Mechanics and Mining Sciences, 2006, 43(4): 634－639.

[15]薛亚东, 张世平, 康天合. 回采巷道锚杆动载响应的数值分析[J]. 岩石力学与工程学报, 2003, 22(11): 1903－1906.XUE Ya-dong, ZHANG Shi-ping, KANG Tian-he.Numerical analysis of dynamic response of rock bolts in mining roadways[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(11): 1903－1906.

[16]荣耀, 许锡宾, 赵明阶, 等. 锚杆对应力波传播影响的有限元分析[J]. 地下空间与工程学报, 2006, 2(1): 115－119.RONG Yao, XU Xi-bing, ZHAO Ming-jie, et al.Numerical simulating propagation of stress waves in the country rock with bolting[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(1): 115－119.

[17]杨湖, 王成. 弹性波在锚杆锚固体系中传播规律的研究[J]. 测试技术学报, 2003, 17(2): 145－149.YANG Hu, WANG Cheng. Study of propagation law of elastic wave in anchorage system[J]. Journal of Test and Measurement Technology, 2003, 17(2): 145－149.

[18]Waterway Experimental Station, Corps of Engineers.Fundamentals of protective design for conventional weapons[M]. [S. l.]: Department of The Army, 1986.

[19]沈俊, 顾金才, 陈安敏, 等. 岩土工程抗爆结构模型试验装置研制及应用[J]. 地下空间与工程学报, 2007,3(6): 1077－1080.SHEN Jun, GU Jin-cai, CHEN An-min, et al.Development and applications of the model test apparatus on anti-explosion structures in geotechnical engineering[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(6): 1077－1080.

[20]马海春, 顾金才, 张向阳, 等. 喷锚支护洞室抗爆现场试验洞顶位移研究[J]. 岩土工程学报, 2012, 34(2): 369－372.MA Hai-chun, GU Jin-cai, ZHANG Xiang-yang, et al.Displacement at top of underground cavern reinforced by grouted bolts during site explosion resisting tests[J].Chinese Journal of Geotechnical Engineering, 2012,34(2): 369－372.