软岩三轴卸荷流变力学特性及本构模型研究

王 宇 ，李建林，邓华锋，王瑞红

（1. 三峡大学 三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；2. 武汉大学 水利水电学院，武汉 430072）

1 引 言

软岩作为一类特殊的岩体，是在特定环境下具有显著塑性变形的复杂岩石介质，它在各类边坡工程及水利水电工程施工中普遍存在，对边坡、坝基以及地下洞室的稳定性起着控制作用[1－3]。近年来，软岩作为建筑结构物地基的工程越来越多，因而研究软岩的流变力学特性对诸多软岩工程都具有非常重要的工程实践意义。

在国外，早在20世纪30年代，Grgiggs[4]对灰岩、页岩和砂岩等类软岩就进行了蠕变试验，试验结果表明，砂岩和粉砂岩在外荷载达到破坏荷载的12.5%～80%时会产生明显的蠕变变形。Li Yong-sheng[5]对红砂岩、粉砂岩和泥岩等不同岩性的软岩进行单轴压缩蠕变试验，分析岩石材料的蠕变速率随岩性和应力水平的变化规律。Gasc-Barbier[6]对黏土质岩进行了不同加荷方式及不同温度下的三轴蠕变试验，得出其应变率和应变大小均随偏应力和温度的增高而增大，而蠕变率还受加载历史影响。在国内，许宏发[7]、陈渠[8]分别对软岩进行了单轴和三轴压缩蠕变试验，探讨了软岩变形、变形速率与时间的依存关系，提出了长期弹性模量和长期损伤变量的概念。刘光廷[9]在多轴应力条件下进行软岩流变试验，考虑干燥、饱水及侧压力等各种因素下砾岩流变对坝体应力的影响。

流变本构模型作为岩石流变力学理论的核心内容，是当前岩石力学研究的重难点之一。Chan[10]提出了一种盐岩蠕变损伤断裂多机制耦合模型，该模型能较好地描述盐岩的蠕变损伤特性。Yahya[11]依据 Von Miss屈服准则和相关流动法则建立了以内部状态变量表述的盐岩流变方程，引入了一个损伤变量，进而推导出一个能够描述软岩的硬化、软化变形特征的流变模型。曹树刚[12]、张向东[13]、范庆忠[14]对软岩进行了单轴和三轴蠕变试验，探讨了与时间有关的软岩一维和三维的本构方程和蠕变方程，全面反映了软岩真实的三阶段蠕变试验规律。韦立德[15]对盐岩进行了蠕变规律试验研究，建立了基于细观力学的盐岩蠕变损伤本构模型。经过数十年的研究，岩石力学与工程界关于软岩流变本构模型的理论研究已经积累了一定的研究成果，但研究涉及的岩体类型较少，研究的范围及深度仍有待提升。

鉴于此，本文以典型软岩－泥质粉砂岩为研究对象，采用恒轴压、分级卸围压的方式对其进行三轴卸荷流变试验，对软岩的卸荷流变力学特性进行深入研究，并提出了一个能较好反映卸荷流变非线性特征的非线性损伤流变本构模型。

2 软岩试样基本力学特性

卸荷流变试验与常规试验均采用同一批泥质粉砂岩，试样加工为直径φ50 mm，高度为100 mm的标准圆柱体试件，自然风干。通过X射线衍射矿物分析可知，其矿物成分为：蒙脱石15%、绿泥石5%、伊利石5%、石英33%、长石15%、方解石25%、白云石 2%。在进行卸荷流变试验之前，首先进行试样筛选，采用声波探测仪测定试样的纵波波速，本次试验岩样的声波纵波波速为1 305～1345 m/s，平均值为1 325 m/s。首先对软岩试样进行常规三轴压缩试验，不同围压下的软岩常规三轴试验结果如表1所示。

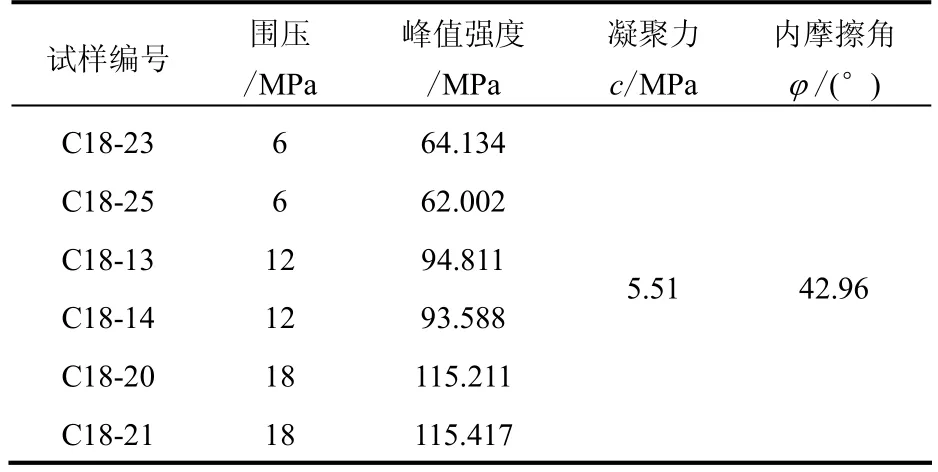
表1 常规三轴压缩试验结果Table 1 Results of triaxial compressive test

3 卸荷流变试验设计及试验成果

3.1 试验设备

本次卸荷流变试验在 RLW-2000 岩石三轴流变试验机上进行。该试验系统由轴向加载系统、围压加载系统、伺服系统、控制系统、数据采集和自动绘图系统等部分组成。轴向、围压加载系统的控制部分采用德国原装全数字EDC控制器，具有加载分辨率高、加载平稳、控制波动度较小等优点，可采用力控制或变形控制，数据采集系统软件在WINDOWS操作平台上运行，可自动进行数据处理。试验系统最大负荷为2 000 kN，位移测量范围0～20 mm，变形测量范围轴向0～5 mm，径向0～2 mm，围压测量范围 0～50 MPa，试样尺寸φ50 mm×100 mm和φ75 mm×150 mm。试验在具有恒温、恒湿条件的流变专用实验室进行，室内温度始终控制在(20±1)℃。

3.2 试验方案设计

本次试验采用轴压恒定，分级卸载围压的方式，卸荷流变试验过程中的恒定轴压值约取常规三轴压缩峰值强度的70%，试验过程分以下3个阶段：①首先按静水压力条件以0.05 MPa/s的加载速率逐步施加σ1=σ3至预定值（6、12、18 MPa）；②保持围压恒定，继续以500 N/s的加载速率加载轴压至预定应力值（46、66、80 MPa）；③保持轴压恒定，以0.05 MPa/s的加载速率分级卸载围压，每级卸载后的围压下均需观察到试样的流变变形趋于稳定后再进行下一级围压卸载，直至试样发生流变破坏。本次试验采用的应力分级方案如表2所示。

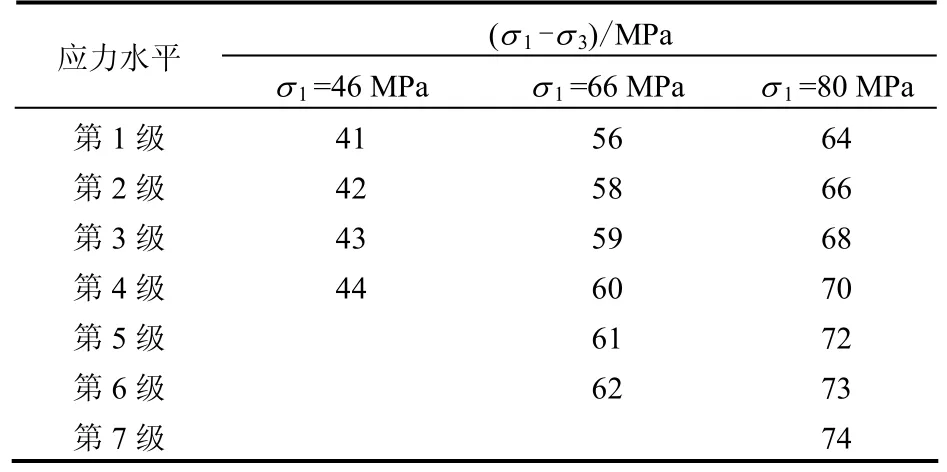
表2 卸荷流变试验偏应力加载方案Table 2 Deviatoric stress loading scheme of unloading rheological test

3.3 试验结果分析

根据设计的卸荷流变试验方案，得到不同应力水平下的试样卸荷流变试验成果，整理后给出轴向应力分别为 66、80 MPa，初始围压分别为 12、18 MPa下的流变曲线如图1、2所示。图中蓝色曲线上方标明的10 MPa等表示各级卸荷流变过程中的恒定围压，下方标明的48 h表示各级卸荷流变持续的时间。图中侧向应变以水平指向试样内部为正，水平指向试样外部为负。同时，以试样c18-15为例，统计了各级恒定围压条件下的轴向及侧向应变变化规律如表3所示。根据流变曲线及表3的统计结果可以看出，软岩试样卸荷流变特性表现为：

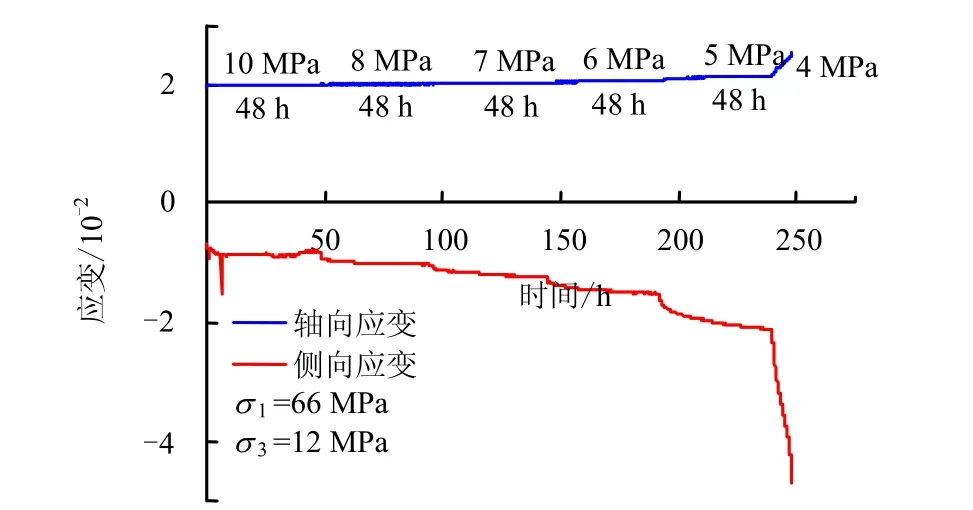
图1 轴向应力σ 1 =66 MPa逐级卸围压流变曲线（试样c18-15）Fig.1 Rheological curves when confining pressure gradually unloading at σ 1 =66 MPa (c18-15)

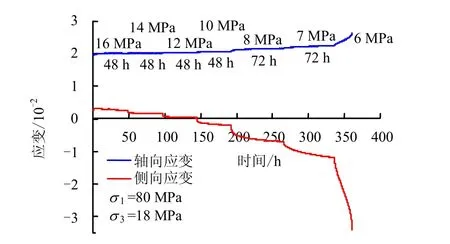
图2 轴向应力σ 1 =80 MPa逐级卸围压流变曲线（试样c18-4）Fig.2 Rheological curves when confining pressure gradually unloading at σ 1 =80 MPa (c18-4)

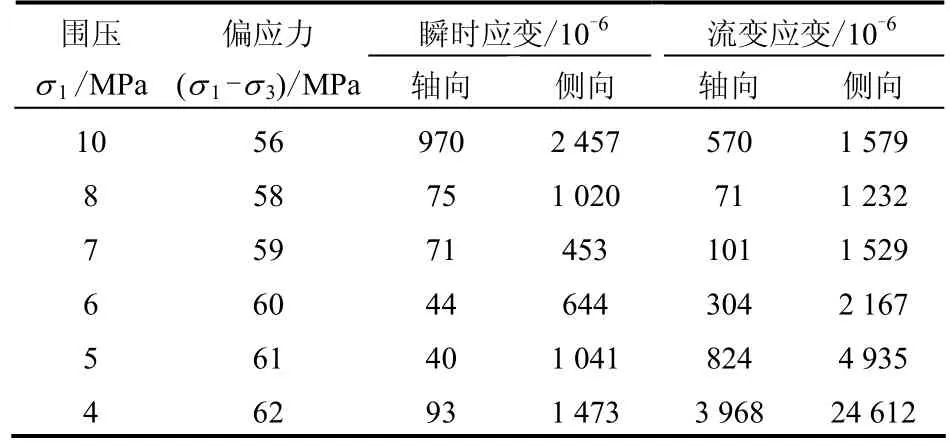
表3 卸荷流变试验成果统计（试样c18-15）Table 3 Statistical results of unloading rheological tests (c18-15)

（1）从图1、2可知，试样在各级恒定围压下均经历了瞬时流变及稳态流变阶段，而在破裂围压水平下则从稳态流变过渡进入非线性加速流变直至破裂，这与三轴压缩流变的曲线特征是一致的。

（2）如表3所示，在各级恒定围压条件下，试样侧向瞬时及流变应变约为轴向的2.5～15倍，说明卸荷流变试验中，试样侧向变形特性较轴向更为显著，侧向扩容效应明显，这与常规三轴流变试验时的变形规律有所不同[16]。

（3）随着围压的逐级降低，侧向流变应变较轴向增大较大，如试样c18-15在恒定轴压66 MPa、围压7 MPa时，轴向和侧向的流变应变相比于前一级的增幅分别为42.3%和24.1%；当卸荷至6 MPa时，轴向和侧向的流变应变增幅分别为 201.0%和41.7%；当卸荷至5 MPa时，轴向和侧向的流变应变增幅分别为171.1%和127.7%；当卸荷至4 MPa时，轴向和侧向的流变应变增幅分别为 381.6%和398.7%。由此可知，卸荷流变下的侧向流变变形发展较轴向快。

结合试样卸荷流变曲线特征可以看出，在最后一级破裂围压下，试样的轴向及侧向流变变形表现出与前几级不同的特征，由此，计算出流变曲线对应的各时刻斜率，得到岩石材料流变过程中流变速率与时间的关系曲线。图 3给出了应力水平为66 MPa时试样在破裂围压为4 MPa下的轴向及侧向流变速率与时间的关系。

由图3可知，试样的轴向流变速率变化规律反映出试样的轴向变形仅经历了稳态流变和非线性加速流变2个阶段，其中稳态流变阶段历时7.7 h，占总时间的 96.2%，相应的稳态流变平均速率为0.046×10-2mm·h-1；侧向流变速率变化规律反映出试样的侧向变形经历了瞬时衰减流变、稳态流变及非线性加速流变3个阶段，其中稳态流变阶段历时7.2 h，占总时间的90.1%，相应的稳态流变平均速率为0.24 ×10-2mm·h-1。上述分析表明，加速流变全过程中，稳态流变在试样的轴向及侧向流变变形过程中均为主要阶段，历时较长，但变形量较小。在破裂围压下，试样的侧向稳态流变平均速率约为轴向的5倍，这表明侧向流变变形在破裂围压下较轴向发展更为迅速，呈现出显著的侧向扩容。不仅如此，在进入加速流变阶段时，试样的轴向及侧向流变速率均迅速非线性增大，试样破裂历时很短，故应特别注意和重视该阶段的流变变形及速率特征。

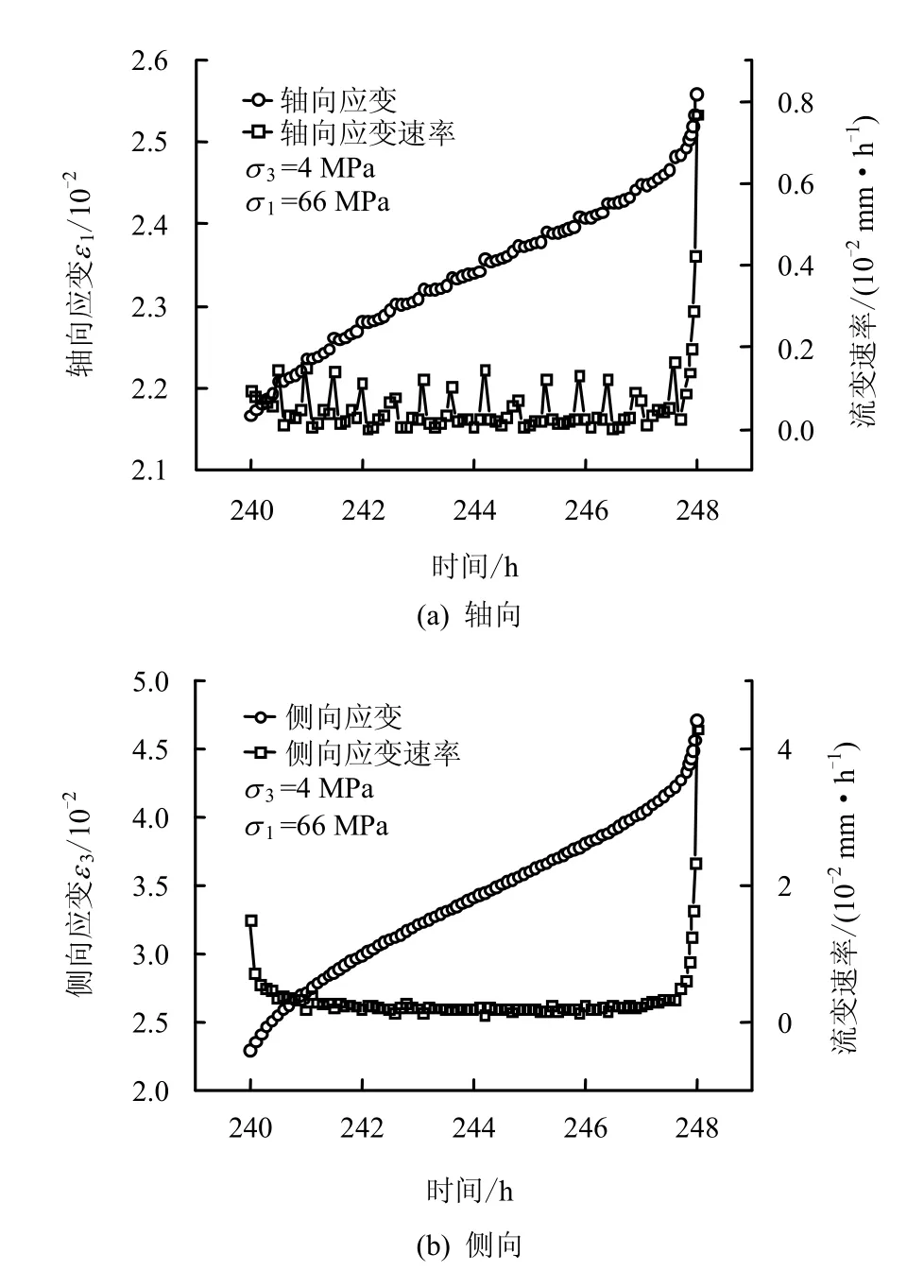
图3 轴向及侧向流变速率与时间的关系（试样c18-15）Fig.3 Relationships between rheological rate and time at axial and lateral directions (c18-15)

4 非线性损伤流变模型及参数辨识

4.1 非线性损伤流变模型

采用Boltzmann叠加原理对分级卸围压所得软岩轴向及侧向变形试验数据进行了整理，以便综合考虑试样的整体变形，并应用线性 Burgers流变模型对试验数据进行了拟合，试验数据及拟合曲线如图4所示，图中曲线附近数据为各级恒定围压值。

根据整理的流变试验曲线可以看出，在各级恒定围压下，试样均经历了初期衰减流变阶段和稳态匀速流变阶段，但在破裂围压下，试样从稳态匀速流变阶段过渡进入非线性加速流变阶段直至破坏。这一非线性加速流变阶段的出现主要是由于岩石材料中存在各种初始裂隙、孔洞及位错，当卸荷至较低围压后，这些初始损伤将经历一系列的演化扩展过程，岩石内部矿物颗粒介质发生晶粒滑移，导致岩石材料内部损伤的几何组构特征随之变化，进而使岩石变形呈非线性增长。而如图 5所示，基于Burgers模型的拟合曲线能较好地描述流变曲线的初始衰减流变和稳态匀速流变阶段，但对于非线性加速流变阶段的应变特征无法较好地反映。

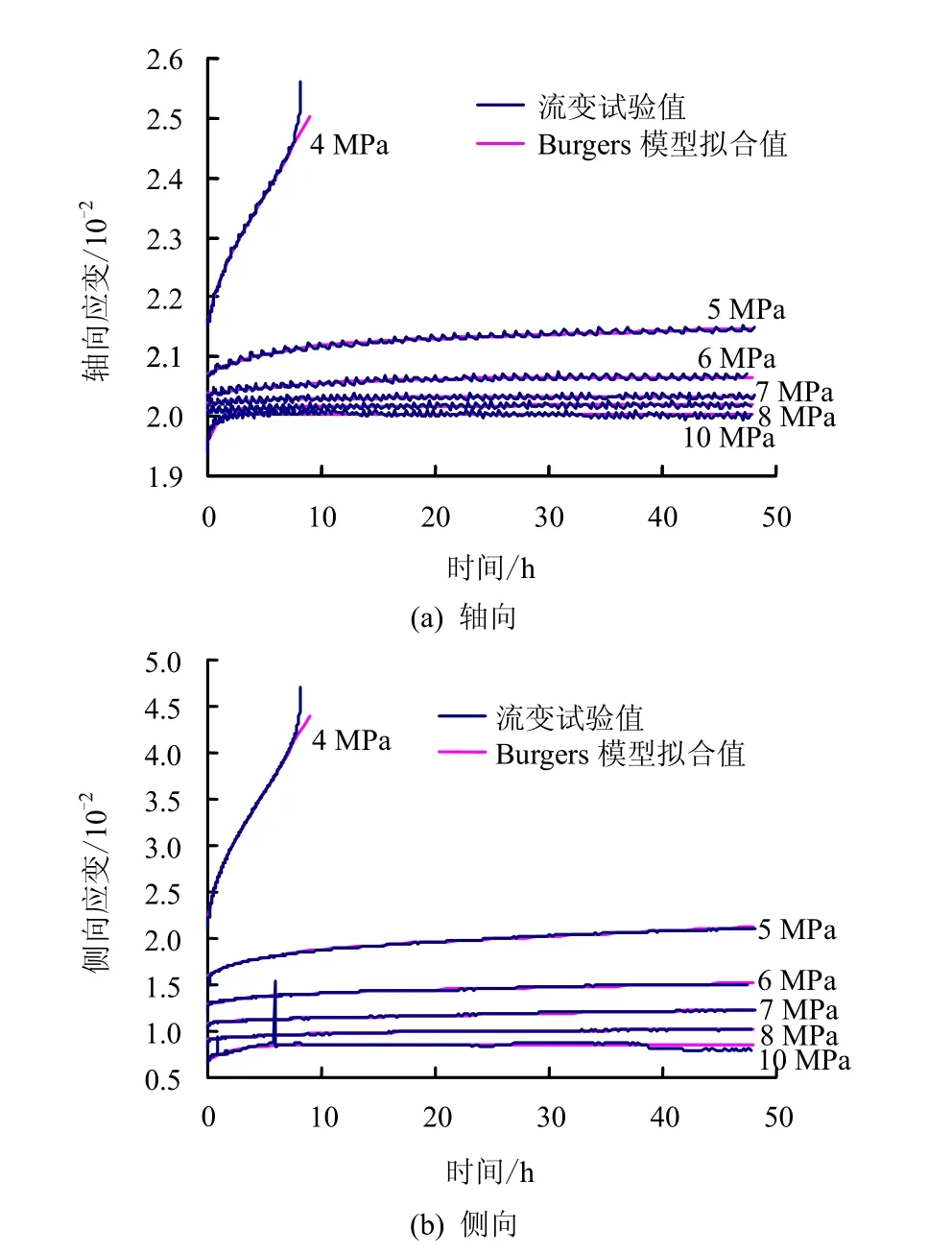
图4 试验数据及Burgers模型拟合曲线（试样c18-15）Fig.4 Rheological test data and fitting curves by Burgers rheological model (c18-15)

鉴于此，假定加速流变阶段岩石应变微元破坏服从Weibull分布，其分布函数为

实际补浇用材质均为低C、S、P的材质，目的是希望能够减弱冒口下成分偏析，模拟浇注时始终使用的都是同种材质。先按照以往铸造厂补浇的习惯操作，次数设定为一次，补浇钢液温度1590℃，重量为冒口高度的2/5的重量。设定补浇距离首次浇注的时间间隔为2h，观察补浇钢液对型腔内原有钢液的温度场影响，以及对冒口内缩孔高度的影响。根据观察结果，优化调整冒口尺寸及补浇方案。

且F(t)应为介于0和1之间的增函数，为此引入φ(t)形式为

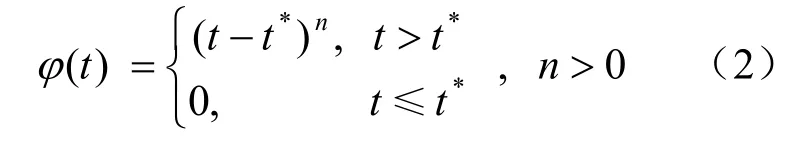
可以得出，岩石在经过时间t的加速流变后，内部损伤变量为

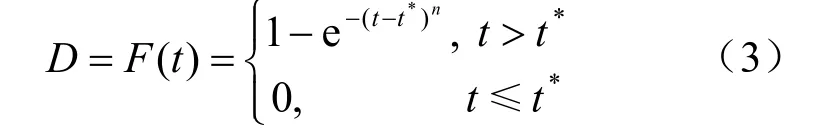
式中：D为损伤因子；t为流变时间；t*为试样从稳态匀速流变进入非线性加速流变的起始时刻。当时间t≤t*时，岩石试样处于稳态流变阶段，试样内部在恒定的应力水平下产生了渐进式的累积损伤，但还未进入突发式的贯通破裂损伤，此时假定损伤因子D趋近于0；当时间t ＞t*时，岩石试样越过稳态流变阶段进入了非线性加速流变阶段，此时，认为损伤因子D随时间t趋于∞而逐步趋近于1。

以 Burgers流变模型为基础，通过考虑损伤建立了一个新的非线性损伤流变模型如图5所示。模型中σs为破裂应力水平的前一级偏应力值，当模型中只有 1和 2部分起作用时，该模型就蜕变为Burgers流变模型。

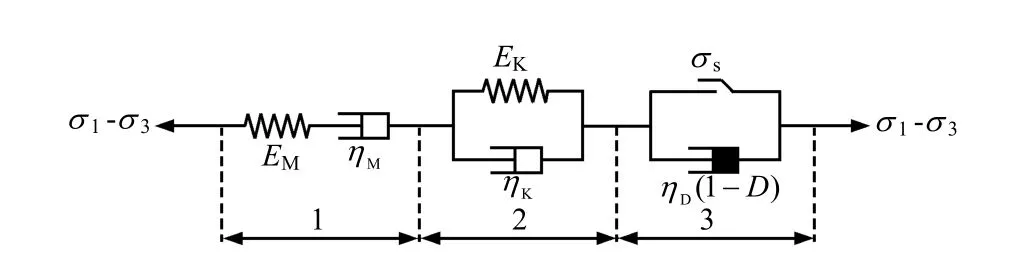
图5 非线性损伤流变模型Fig.5 Nonlinear damage rheological model

当应力0＜(σ1-σ3)＜σs时，模型中只有1和2部分起作用，模型蜕变为 Burgers线性流变模型，相应的状态方程为

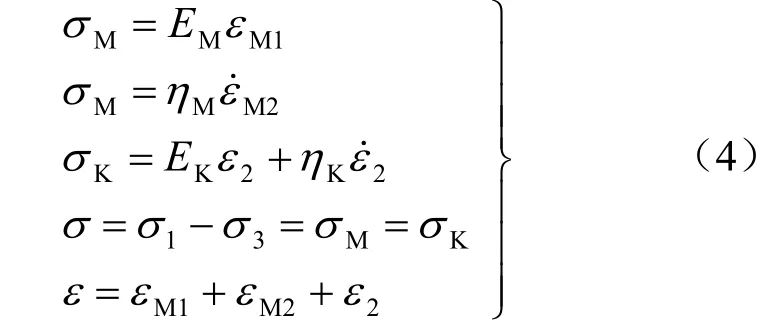
式中：σM和σK分别表示图5中第1部分及第2部分的应力值；εM1和ε˙M2分别表示第1部分中弹性元件及黏性元件的应变量；εM2同ε˙M2；ε˙2表示第2部分中黏性元件的应变量。

对式（4）进行相应的拉普拉斯变换及其逆变换则相应的一维流变本构方程为

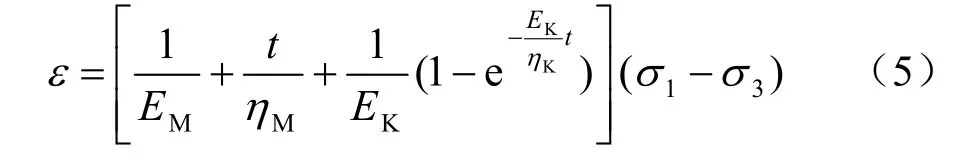
当应力0＜σs＜(σ1-σ3)，且t ≤ t*时，3部分中的非线性损伤因子不起作用，相应的状态方程为

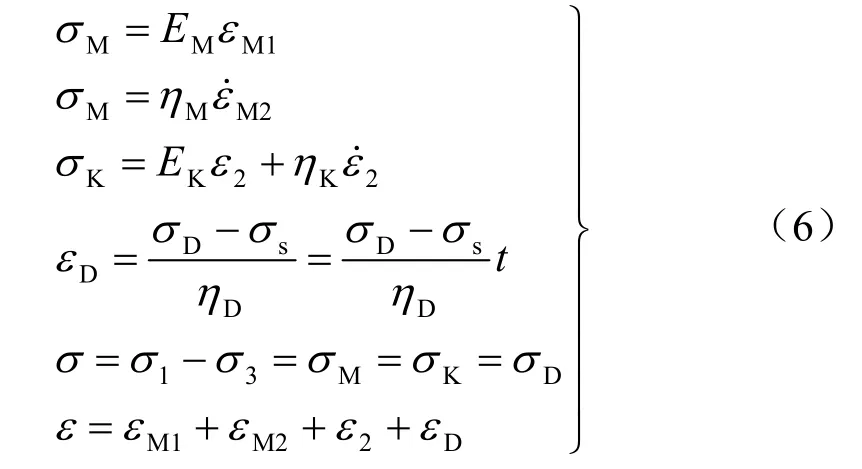
式中：εD表示第3部分对应的应变量；ηD表示损伤元件不起作用时的黏滞系数。

对式（6）进行相应的拉普拉斯变换及其逆变换，可得相应的一维流变本构方程为

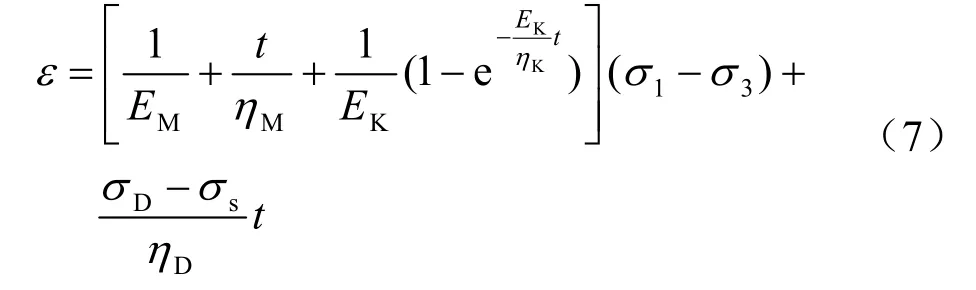
当应力0＜σs＜(σ1-σ3)，且t ＞ t*时，模型各部分及损伤因子D均起作用，相应的状态方程为

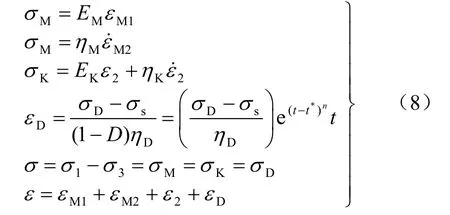
对式（8）进行相应的拉普拉斯变换及其逆变换，可得相应的一维流变本构方程为

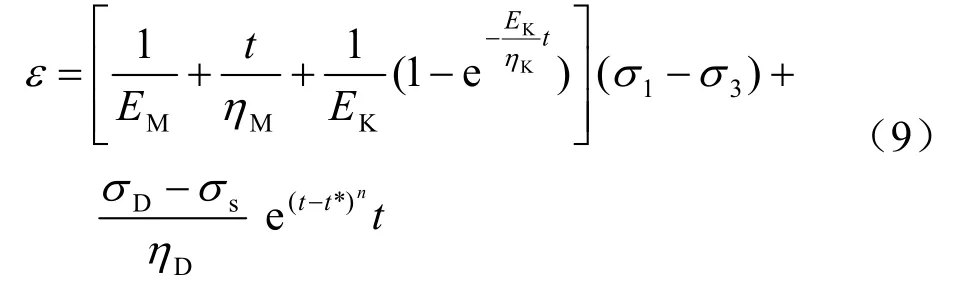
式中：下角标“M”、“K”与“D”分别表示 Maxwell体、Kelvin体与非线性损伤体对应的力学分量；EM、ηM、EK、ηK分别为Maxwell体和Kelvin体的弹性模量与黏滞系数；σD为模型第3部分的应力值；n反映试样非线性加速阶段流变速率的大小。

4.2 模型的参数辨识与验证

利用软岩试样不同应力水平下三轴卸荷流变曲线在破裂围压下的加速流变全过程试验数据，采用Levenberg-Marquardt非线性优化最小二乘法对非线性损伤流变模型进行验证，并辨识得到相应的模型流变力学参数如表4所示。

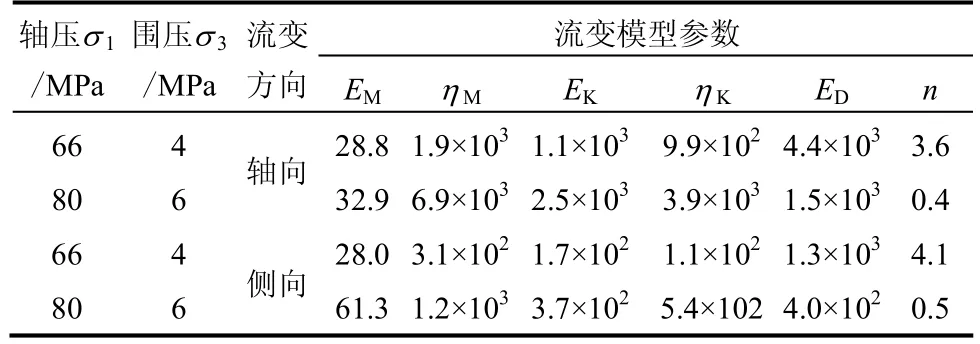
表4 非线性损伤流变模型参数Table 4 Parameters of nonlinear damage rheological model

图6、7给出了破裂围压下的加速流变全过程试验结果与建立的非线性损伤流变模型的对比。

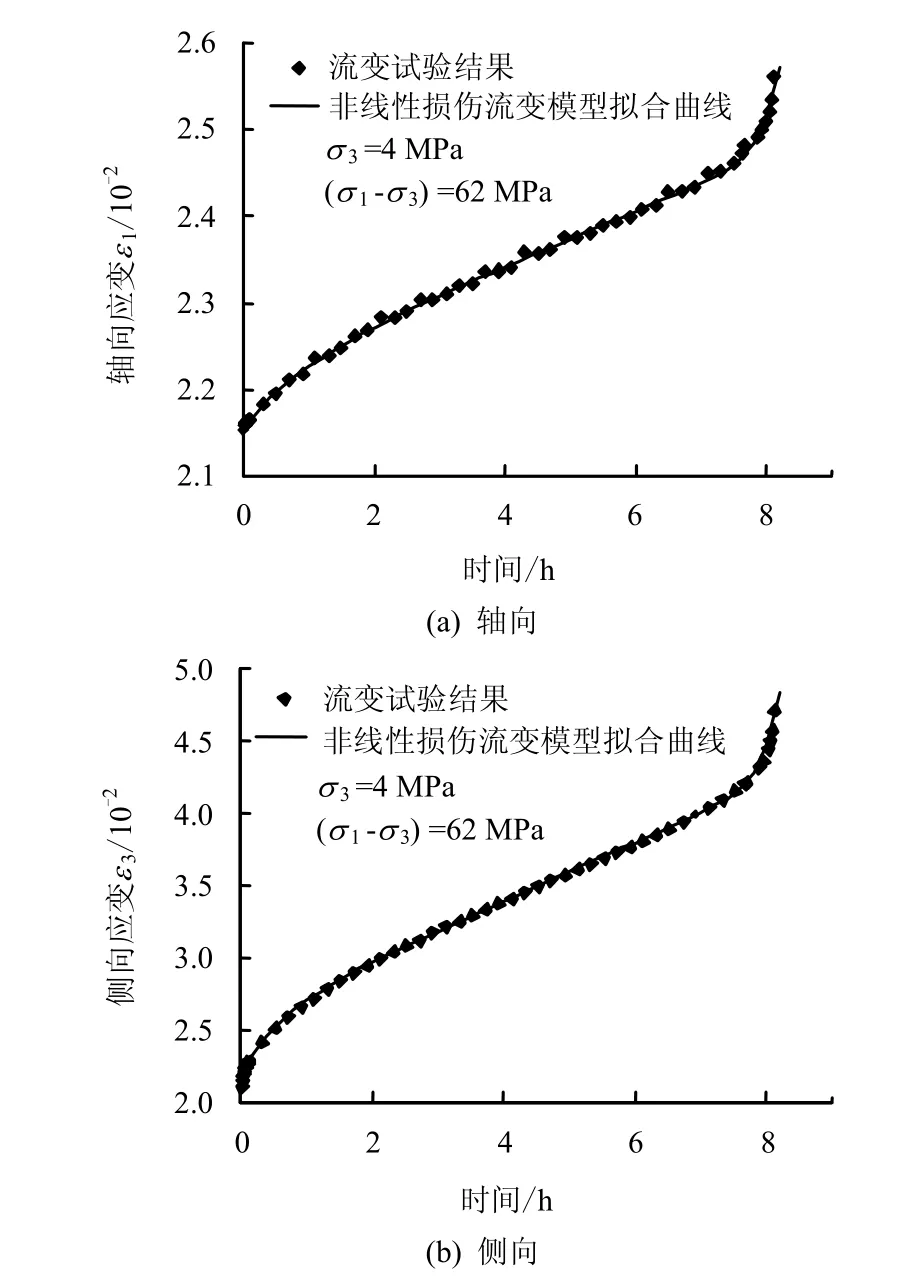
图6 非线性损伤流变模型与试验结果的对比（σ 1 =66 MPa，σ 3 =12 MPa）Fig.6 Comparison between nonlinear damage rheological model and experimental result (σ 1 =66 MPa, σ 3 =12 MPa)

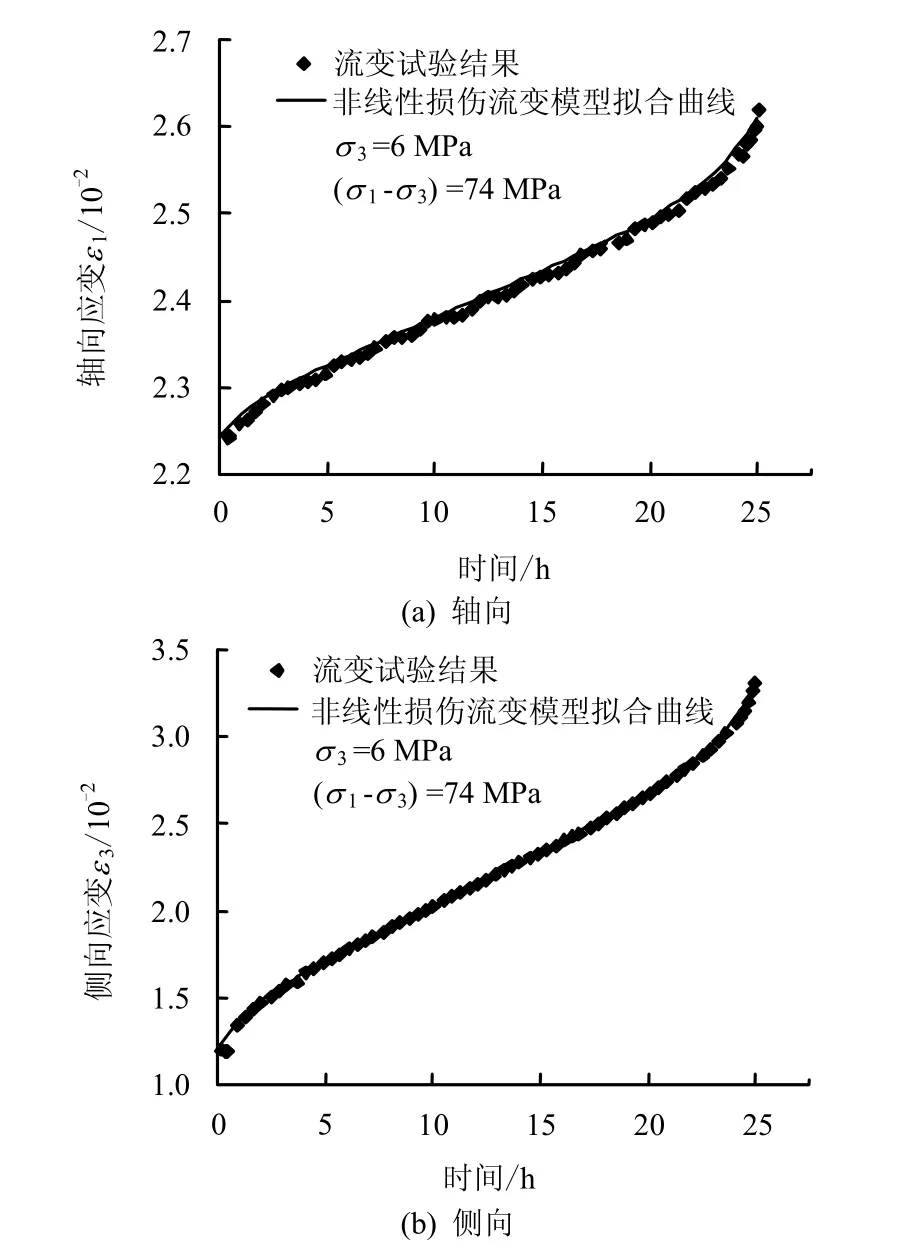
图7 非线性损伤流变模型与试验结果的对比（σ 1 =80 MPa，σ 3 =18 MPa）Fig.7 Comparison between nonlinear damage rheological model and experimental result(σ 1 =80 MPa, σ 3 =18 MPa)

由图可见，相比 Burgers模型而言，该非线性损伤流变模型能很好地反映加速流变全过程的各阶段，很好地体现了流变曲线的非线性特征。模型拟合曲线与试验结果吻合程度很好，这说明本文中建立的这一非线性损伤流变模型是正确合理的。

5 结 论

（1）各级恒定围压下，试样侧向瞬时及流变应变约为轴向的2.5～15倍，即试样在卸荷流变条件下侧向变形特性较轴向更为显著，侧向扩容效应明显，表现出与常规三轴流变试验时不同的变形规律。不仅如此，卸荷流变下的侧向流变变形发展要较轴向快。

（2）破裂围压下的试样加速流变全过程曲线表明，稳态流变在试样的轴向及侧向流变变形过程中均为主要阶段，且该阶段试样的侧向稳态流变平均速率约为轴向的5倍，表明侧向流变变形在破裂围压下较轴向发展更为迅速；而进入加速流变阶段后，试样的轴向及侧向流变速率均迅速非线性增大，试样破裂历时很短，故工程实践中应特别注意和重视该阶段的流变变形及速率特征。

（3）以 Burgers流变模型为基础，建立了一个新的非线性损伤流变模型，并采用该模型对不同应力水平下的软岩试样加速流变全过程曲线进行了辨识，得到了该模型下的流变参数，流变模型曲线与试验结果吻合程度很高，表明建立的非线性损伤流变模型是正确合理的。

[1]孙钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999.

[2]刘特洪, 林天健. 软岩工程设计理论与施工实践[M].北京: 中国建筑工业出版社, 2001.

[3]熊诗湖, 邬爱清, 周火明. 层状软岩力学特性现场试验研究[J]. 地下空间与工程学报, 2006, 2(12): 887－890.XIONG Shi-hu, WU Ai-qing, ZHOU Huo-ming. In-situ test on mechanical characteristics of soft layer rock mass[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(12): 887－890.

[4]GRIGGS D T. Creep of rocks[J]. Journal of Geology,1939, 47(3): 225－251.

[5]LI Yong-sheng, XIA Cai-chu. Time-dependent tests on intact rocks in uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2000,37(3): 467－475.

[6]GASC-BARBIER M, CHANCHOLE S, BÉREST P.Creep behavior of Bure clayey rock[J]. Applied Clay Science, 2004, 26(1－4): 449－458.

[7]许宏发. 软岩强度和弹性模量的时间效应研究[J]. 岩石力学与工程学报, 1997, 16(3): 246－251.XU Hong-fa. Time-dependent behaviors of strength and elasticity modulus of weak rock[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(3): 246－251.

[8]陈渠, 西田和范, 岩本健. 沉积软岩的三轴蠕变实验研究及分析评价[J]. 岩石力学与工程学报, 2003, 22(6):905－912.CHEN Qu, NISHIDA Kazunori, IWAMOTO Takeshi.Creep behavior of sedimentary soft rock under triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(6): 905－912.

[9]刘光廷, 胡显, 陈凤岐. 软岩多轴流变特性及其对拱坝的影响[J]. 岩石力学与工程学报, 2004, 23(8): 1237－1241.LIU Guang-ting, HU Xian, CHEN Feng-qi. Rheological property of soft rock under multiaxial compression and its effect on design of arch dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1237－1241.

[10]CHAN K S, MUNSON D E, BODNER S R. Creep deformation and fracture in rock salt[C]//Fracture of Rock.Boston: Southampton WIT Press, 1999.

[11]YAHYA O M L, AUBERTIN M, JULIEN M R. A unified representation of the plasticity creep and relaxation behavior of rock salt[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 787－800.

[12]曹树刚, 边金, 李鹏. 软岩蠕变试验与理论模型分析的对比[J]. 重庆大学学报, 2002, 25(7): 96－98.CAO Shu-gang, BIAN Jin, LI Peng. Comparison research of creep experiments and the analysis of the theoretical model of soft rocks[J]. Journal of Chongqing University, 2002, 25(7): 96－98.

[13]张向东, 李永靖, 张树光. 软岩蠕变理论及其工程应用[J]. 岩石力学与工程学报, 2004, 23(10): 1635－1639.ZHANG Xiang-dong, LI Yong-jing, ZHANG Shu-guang.Creep theory of soft rock and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(10): 1635－1639.

[14]范庆忠, 高延法. 软岩蠕变特性及非线性模型研究[J].岩石力学与工程学报, 2007, 26(2): 391－396.FAN Qing-zhong, GAO Yan-fa. Study of creep properties and nonlinear creep model of soft rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(2): 391－396.

[15]韦立德, 杨春和, 徐卫亚. 基于细观力学的盐岩蠕变损伤本构模型研究[J]. 岩石力学与工程学报, 2005,24(23): 4253－4258.WEI Li-de, YANG Chun-he, XU Wei-ya. Study of creep damage constitutive model of salt rock based on mesomechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(23): 4253－4258.

[16]徐卫亚, 杨圣奇, 杨松林. 绿片岩三轴流变力学特性的研究(I): 试验结果[J]. 岩土力学, 2005, 26(4): 531－537.XU Wei-ya, YANG Sheng-qi, YANG Song-lin.Investigation on triaxial rheological mechanical properties of green schist specimen(I): Experimental results[J].Rock and Soil Mechanics, 2005, 26(4): 531－537.