基于剪切滑移的圆形洞室应力状态研究
李 杰,李文培, ,施存程, ,王德荣,范鹏贤
(1. 解放军理工大学 爆炸冲击防灾减灾国家重点实验室,南京 210007;2. 海军工程设计研究局,北京 100070;3. 第二炮兵指挥学院 五系,武汉 430012)
1 引 言
地下工程的应力、应变状态分析是岩土力学的一个基本问题,是隧道、采矿通道以及钻井等工程初步设计的重要依据,也是验证数值结果及软件的重要方法。过去许多研究者从不同的岩体力学特性得出许多圆形洞室的解析解[1-5]。这些力学特性包括相关和不相关塑性流动法则、应变软化、脆性、黏性、剪胀和构造缺陷等。广泛使用的材料模型有弹性-理想塑性模型、弹-脆-塑性模型、弹性-应变软化模型等,此外用分段曲线逼近实测岩石应力-应变全本构曲线也是一种途径[6]。应用较广泛的屈服或破坏准则有Mohr-Coulomb准则、Hoek-Brown强度准则、Drucker-Prager强度准则和统一强度理论等[5, 7-10]。
岩石内包含各种尺度的孔隙、微裂缝甚至裂缝等缺陷,并不均匀连续,特别在峰后出现剪切应变局部化现象,位移场将出现间断。文献[11]采用光滑函数组合来描述岩石间断位移场变形特征并得出相应控制方程。将其应用于圆形坑道开挖中,考虑滑移面上不同的应力-滑移关系,研究了圆形坑道围岩稳定性问题[12-13]。文献[14]给出一个非连续平面应变弹塑性模型,并用Fortran语言编写局部剪切变形有限元程序,通过简单算例与传统连续介质理论弹性结果进行比较。但这种比较还不充分,需推导一种非连续模型弹塑性解析解来进一步比较验证。
本文引入圆形洞室非连续数学模型[12-13],推导得到开挖后应力状态的非连续表达式。研究了围岩的应力分区情况并得到了各分区中应力值。通过引入边界条件来确定荷载参数,解决了荷载参数不确定的问题。进一步根据围岩中应力分布状态确定荷载参数取值范围,并得出围岩应力分布图。将其与研编的有限元程序数值解比较验证。该解析考虑了岩石变形破坏的物理本质,可作为工程设计的依据以及数值计算验证的方法。
2 圆形洞室非连续数学模型
陈士林等[12]将岩石滑移线上的非线性本构关系应用于圆形洞室围岩的计算中,结合平面应变极坐标的动量守恒方程,利用对称原理得出了在极坐标系(r,θ )下圆形洞室的计算模型:

进而利用该模型推导得出了圆形洞室围岩应力状态非连续解为:

洞室开挖后,原始围岩中的应力平衡被破坏,其应力状态将发生巨大改变,通过变形围岩应力逐步向洞室围岩深处转移,并且最后达到一个新的平衡。图1给出了洞室围岩应力状态分布示意图,图中为洞室半径,为塑性软化区半径,为残余强度区半径,为未扰动区域岩石初始地应力。

图1 围岩应力状态分区Fig.1 Distribution of stress state for surrounding rock
对式(1)进行积分变换可得

由式(4)可确定函数τ(r,p),滑移量δ(τ)具有长度量纲,需要通过试验确定。应力–滑移量的变化规律与外摩擦的变化规律近似,可以应用研究外摩擦的类似方法间接地确定应力–滑移量图[16]。
当围岩的剪切应力-滑移关系如图2所示时,结合式(4)可得到应力状态分区半径分别为
从图1中可以看出,随着荷载参数的变化,洞室围岩可以出现3个不同的分区:弹性区、塑性软化区以及残余强度区。利用式(4)结合图2可得到应力表达式:

图2 剪切应力与滑移的关系Fig.2 Relationship between shear stress and slip
由式(6)~(8)可见,剪切应力τ =τ( r, p )是一个不定值,随着距圆形洞室中心的距离而变化,并受荷载参数p的影响,不同的荷载参数决定围岩处于何种应力状态。
为了分析方便引入无量纲参数:

洞室挖只影响到周围一定范围内的岩石,这部分岩石简称为围岩,围岩以外的岩石仍保持原始应力状态。在这里围岩的半径用R 表示,大量研究表明,洞室开挖的影响主要集中在10倍开挖半径范围内,超出这个范围,开挖的影响很小,可忽略。因此,可假定围岩深部应力为原始地应力作为边界条件。即

利用无量纲参数可将式(5)转化为:
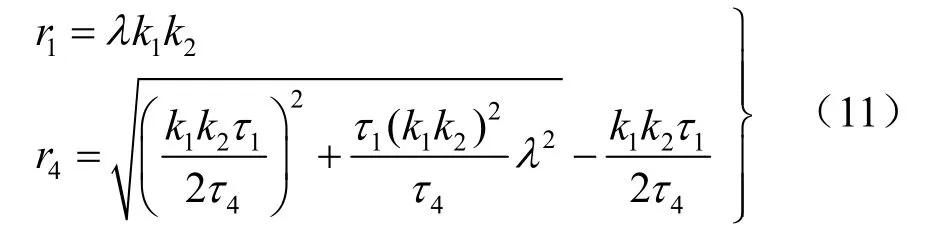
由式(11)可知,洞室围岩残余区和软化区半径不仅和岩石的性质有关,还取决于荷载参数λ。
3 圆形洞室围岩应力状态非连续解析
下面将对圆形洞室围岩应力状态非连续解进行分析。在深部条件下,围岩初始压力很大,这样体积力影响就相对较小,故忽略体积力Xr的影响,同时令这样式(2)可简化为:

在这里只考虑开挖后围岩不支护的情况,此时围岩的内压力为0,即 σrr(r0)= 0。
3.1 只出现弹性应力状态情况
当0 ≤ λ<m2,此时有 r1<r0,说明洞室围岩处于完全弹性状态,

将式(13)代入到式(12)中可得出该条件下围岩的应力状态为:
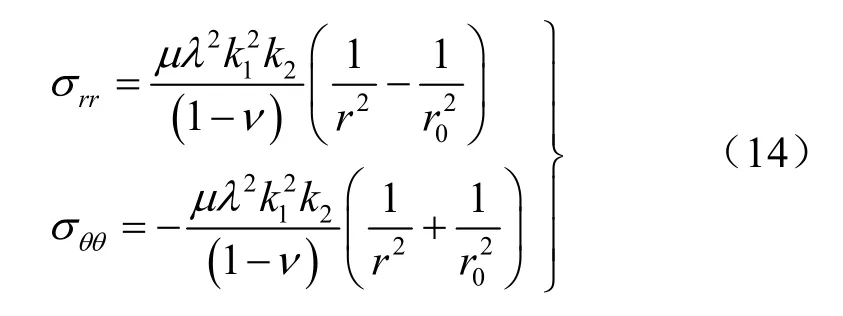
在式(14)中荷载参数λ是未知的,需要通过边界条件来确定。
下面通过一个算例来说明问题,在初始地应力为20 MPa的岩石中开挖一个半径为2 m的圆形洞室。剪切模量μ=5 GPa,泊松比ν=0.3,初始剪切强度τ1=7.5 MPa,残余剪切强度τ4=1.5 MPa,滑移 长 度k1=0.05 m, k2= μ/ (1- ν )τ1, 重 度 γ=25 kN/m3。
计算可知,围岩的径向和法向应力都出现了集中,集中系数为2.0,与弹性理论解符合。随距洞室中心距离的增大,围岩中应力渐接近初始应力状态。
3.2 出现两个应力状态分区情况
(1)在软化区, r0≤ r<r1,此时有:
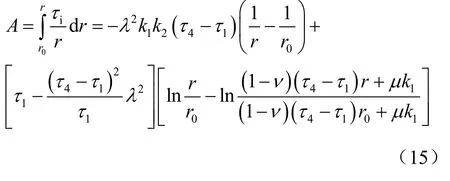
将式(15)代入式(12)得到

(2)在弹性区, r1≤ r ,此时有

将式(18)代入式(12)得到

采用前算例,参数不变,可得到围岩中仅存软化区和弹性区时应力状态。图3为围岩分为软化区和弹性区时的应力随距离变化图。从图中可知,径向应力σrr在洞室周围减小为0,随着距离的增大逐渐回复到原始应力;环向应力σθθ在洞室周围有松弛,逐步向围岩深处转移,在软化区和弹性区交接面上达到最大,约为1.4倍初始应力,在弹性区又逐步减小到初始应力大小。

图3 洞室围岩比例应力随围岩深度变化图Fig.3 Variations of proportional stresses vs. depth of surrounding rock around circular opening
3.3 出现3个应力状态分区情况
(1)在 r0≤ r<r4区域内为残余强度区,此时有
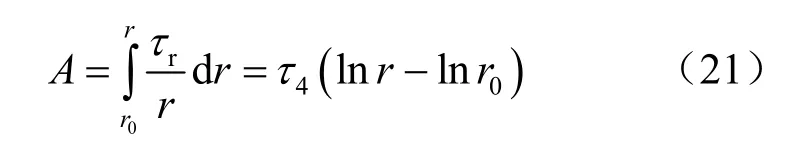
将式(21)代入式(12)得到

(2)在 r4≤ r<r1区域内变成软化区,有
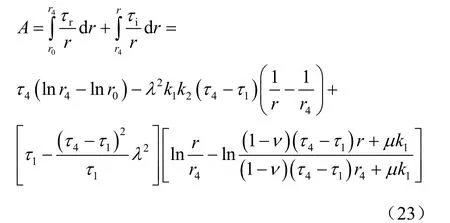
将式(23)代入式(12)得到
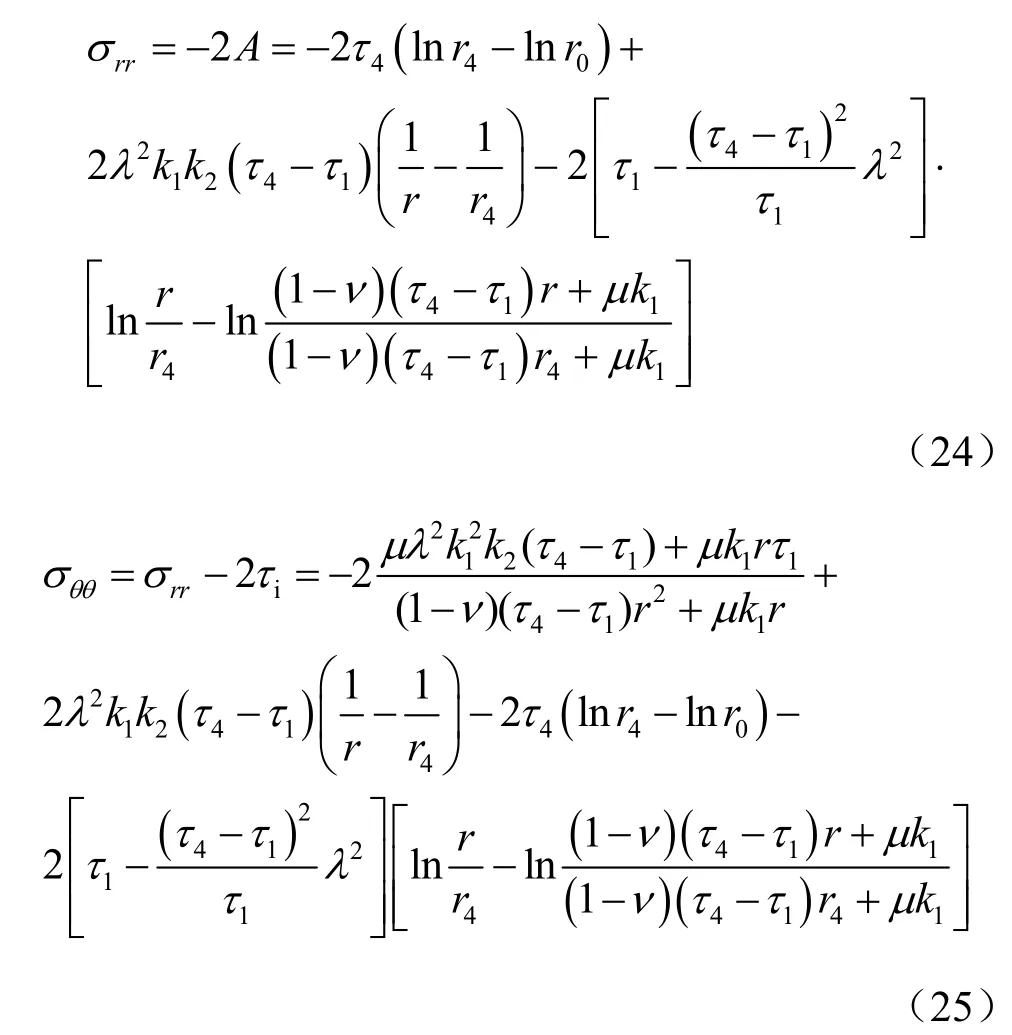
(3)在 r1≤ r 区域内为弹性区,此时有

将式(23)代入式(12)得到

同样,图4为洞室围岩分为3个区时的围岩应力随距离变化图。从图中可以看出,3个分区的应力连续。在残余强度区,围岩的径向和环向应力都很小,说明此处围岩处于一个十分不利的条件,将产生异常的变形,必须及时采取相应的工程处理措施。在软化区内,径向应力σrr在随着距洞室中心距离的增大逐渐回复,达到 0.7σ0;环向应力σθθ也逐步变大,在软化区和弹性区交接面上达到最大,约为1.4倍初始地应力。在弹性区两个方向的应力都逐步回复到初始应力大小。

图4 洞室围岩比例应力随围岩深度变化图Fig.4 Variations of proportional stresses vs. depth of surrounding rock around circular opening
4 比较与讨论
通过前面的分析可知,荷载系数λ对围岩的应力状态影响很大,不同的荷载系数决定了洞室围岩出现几个分区。而真实条件下,围岩只可能处于一个特定的应力状态。由工程实际可知,洞室开挖后,围岩中应力转移是一个渐进的过程。没有开挖前都处于弹性状态;开挖后,在开挖表面应力卸载,洞室周围逐渐进入软化区,当荷载足够大的情况下,洞室周围会进入到残余强度状态。
文献[12-13]研究表明:随着荷载系数λ的变化,洞室围岩中将出现不同的应力状态分区,应力也逐步向围岩深处转移,相应的围岩自身承载能力也将发生变化。围岩自身承载能力的无量纲化表达式可以写成:
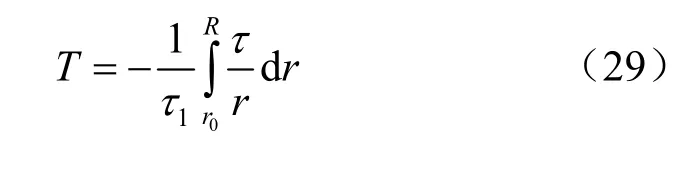
对上述3种不同情况分别计算T并对λ求导,可以得到当λ的取值在范围内时,函数T(λ)有惟一的最大值T(λ*),此时 r4<r0<r1,说明洞室围岩中没有残余强度区出现,只有弹性区和软化区。因此,在围岩初始应力状态没有超过围岩的最大自身承载能力之前,可以认为,此时围岩不会出现残余强度区。残余强度区的出现只能是在围岩外部荷载超过围岩最大自身承载能力的情况,此时应力进一步向围岩深部转移,而围岩的承载能力却有一定降低,这样就形成了一个不稳定的状态,即没有外部能量的输入,变形也将继续开展。因此,在外部荷载没有达到围岩自身最大承载能力之前,式(19)、(20)能够表示当前的应力状态。
通过一个简单算例将编写的有限元程序与非连续解析解相互比较验证。岩石中开挖一个半径为2.5 m的圆形洞室。剪切模量μ=5 GPa,泊松比ν=0.3,初始剪切强度τ1=7.5 MPa,残余剪切强度τ4=1.5 MPa,滑移长度k1=0.05m,k2=μ/ (1- ν)τ1,重度γ=25 kN/m3。利用式(19)、(20)能够计算出此时圆形洞室围岩应力状态解析解。
根据非连续解析解算例的输入数据反推得出有限元程序的岩石参数。从图2中可知,初始黏聚力τ0=τ1, 残 余 黏 聚 力 τr=τ4, 卸 载 模 量Eu=(τ4-τ1)/k1,其他具体参数见表1中。
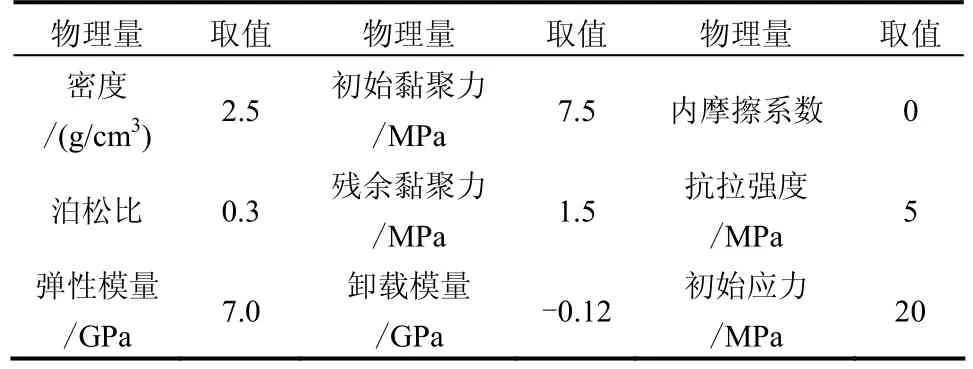
表1 计算所采用岩石参数Table 1 Parameters for rock
图5为有限元程序的数值解与非连续解析解比较图。从图中可以看出,数值解和解析解较一致。两种结果在孔洞周围的应力软化区半径几乎相同,这种表象的应力软化的根源是滑移面上因剪切力超过了岩石的剪切强度而产生沿滑移面的滑移。应力软化区围岩已经发生了剪切滑移破坏,处于峰后变形状态,但由于残余黏结强度及调动起来的摩擦作用,还具有一定的承载能力。在应力软化区的外围是弹性区,由于边界的影响,径向应力在边界附近有很小的误差,可忽略。在软化区和弹性区交接面上环向应力最大,都约为1.4倍初始地应力。
推导的圆形洞室周围应力状态解析解中荷载参数是不确定的,而荷载参数控制着应力分区以及各分区中应力值。本文通过引入边界条件来确定其中的荷载参数,解决了荷载参数不确定的问题,并且得到了不同荷载参数范围的洞室开挖后应力分布图。深入分析得知,在没有超过围岩的极限承载能力时开挖后围岩应力状态为第2种。采用这个应力状态解析解比较验证了有限元程序数值解。
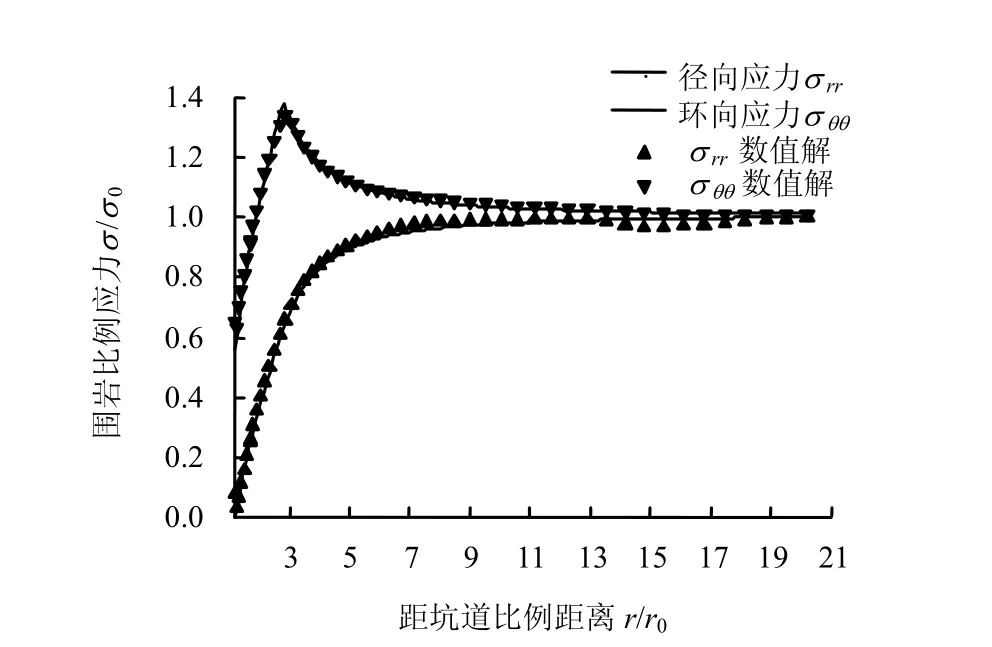
图5 数值解与解析解比较Fig.5 Comparison between analytical solution and numerical solution
5 结 论
(1)荷载参数控制着应力分区以及各分区中的应力值。通过引入边界条件来确定其中的荷载参数,解决了荷载参数不确定的问题。
(2)根据围岩中应力分布状态确定了荷载参数取值范围,并得出不同荷载参数范围内的洞室开挖后围岩应力分布图。采用剪切应力滑移模型来表示岩石的软化十分适合,不仅可在宏观上体现岩石的应力软化力学特性,而且能更好地刻画岩石变形破坏的物理本质。
(3)将推导的圆形洞室开挖后围岩应力分布解析解与局部剪切应变二维有限元程序数值解进行了比较验证,一致性较好。
[1]BROWN E T, BRAY J W, LADANYI B, et al. Ground response curves for rock tunnels[J]. Journal of Geotechnical Engineering, 1983, 109(1): 15-39.
[2]WANG Y. Ground response of circular tunnel in poorly consolidated rock[J]. Journal of Geotechnical Engineering, 1996, 122(9): 703-708.
[3]SHARAN S K. Analytical solutions for stresses and displacements around a circular opening in generalized Hoek-Brown rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(1): 78-85.
[4]蒋斌松, 张强, 贺永年, 等. 深部圆形巷道破裂围岩的弹塑性分析[J]. 岩石力学与工程学报, 2007, 26(5): 982-986.JIANG Bin-song, ZHANG Qiang, HE Yong-nian, et al.Elastoplastic analysis of cracked surrounding rocks in deep circular openings[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 982-986.
[5]CARRANZA-TORRES C. Dimensionless graphical representation of the exact elasto-plastic solution of a circular tunnel in a Mohr-Coulomb material subject to uniform far-field stresses[J]. Rock Mechanics and Rock Engineering, 2003, 36(3): 237-253.
[6]潘岳, 王志强, 王在泉. 非线性硬化与非线性软化的巷道围岩应力分布与工况研究[J]. 岩石力学与工程学报,2006, 25(7): 1343-1351.PAN Yue, WANG Zhi-qiang, WANG Zai-quan. Study of distribution of surrounding rock and work condition of tunnel based on strain nonlinear hardening and softening[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1343-1351.
[7]HOEK E, BROWN E T. Empirical strength criterion for rock masses[J]. Journal of Geotechnical Engineering Division, ASCE, 1980, 106(9): 1013-1035.
[8]ROUAINIA M, WOOD D M. A kinematic hardening constitutive model for natural clays with loss of structure[J]. Geotechnique, 2000, 50(2): 153-164.
[9]KIM M K, LADE P V. Modeling rock strength in three dimensions[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1984, 21(1): 21-33.
[10]昝月稳, 俞茂宏, 王思敬. 岩石的非线性统一强度准则[J]. 岩石力学与工程学报, 2002, 21(10): 1435-1441.ZAN Yue-wen, YU Mao-hong, WANG Si-jing. Nonlinear unified strength criterion of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(10): 1435-1441.
[11]REVUZHENKO A F, SHEMYAKIN E I. Problem of plane strain of hardening and softening plastic materials[J]. Journal of Applied Mechanics and Technical Physics, 1977, 18(3): 406-420.
[12]陈士林, 钱七虎, 王明洋. 深部坑道围岩的变形与承载能力问题[J]. 岩石力学与工程学报, 2005, 24(13): 2203-2211.CHEN Shi-lin, QIAN Qi-hu, WANG Ming-yang.Problems of deformation and bearing capacity of rock mass around deep buried tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(13): 2203-2211.
[13]李文培, 王明洋, 范鹏贤. 基于间断位移场的洞室围岩承载能力研究[J]. 岩土力学, 2010, 31(8): 2441-2447.LI Wen-pei, WANG Ming-yang, FAN Peng-xian. Bearing capacity of tunnel surrounding rock based on discontinuous displacement field[J]. Rock and Soil Mechanics, 2010, 31(8): 2441-2447.
[14]李文培, 王明洋, 范鹏贤, 等. 深部围岩变形与破坏模型及数值方法研究[J]. 岩石力学与工程学报, 2011,30(6): 1250-1257.LI Wen-pei, WANG Ming-yang, FAN Peng-xian, et al.Study of deformation and failure model for deep rock mass and its numerical method[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(6): 1250-1257.
[15]Новожилов В В. Две статьи о математических моделях в механике сплошной среды[J]. ИПМ АН СССР ЛГУ пр, Москва, 1983, 215: 56-60.
[16]NIKIFOROVSKY B S, SHEMYAKIN E I. Dynamic failure of solid bodies[M]. Nauka Novosbirsk: [s. n.],1979.

