关于GA－凸函数的Hadamard型不等式的一个注记

时统业，吴 涵

(海军指挥学院浦口分院，南京 211800)

1 引理

定义 1［1］设 f(x)是定义在区间 I⊂(0，+ ∞)上的连续函数，如果对于任意 a，b∈I和 t∈(0，1)，有

则称f(x)在区间I是GA－下凸的。如果式(1)的不等号反向，则称f(x)在区间I上是GA－上凸的。

文献［2－4］给出关于GA－凸函数的Hadamard型不等式，见定理1。

定理 1［3－4］设 f(x)是［a，b］上的 GA － 下凸函数，则

如果f(x)是［a，b］上的GA－上凸函数，则式(2)的不等式反向。当且仅当f(x)=c+dlnx时等号成立，c、d是常数。

注1 由定理1的证明过程易知

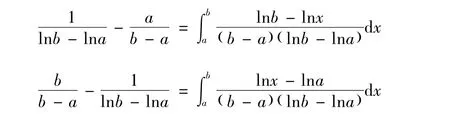
引理1［1］设f(x)是定义在［a，b］⊂(0，∞)上的函数，则f(x)是［a，b］上的GA －下凸函数的充要条件为f(ex)为［lna，lnb］上的下凸函数。

引理 2［5］设 f(x)是［a，b］上的下凸函数，则对任意 x，y∈［a，b］，有

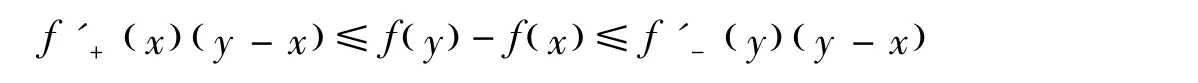
当且仅当f(x)=c+dx时等号成立，c、d是常数。

引理3 设f(x)是定义在［a，b］⊂(0，∞)上的GA－下凸函数，则

1)x f'－(x)和 x f'+(x)在(a，b)单调不减。

2)对任意 x，y∈［a，b］，有

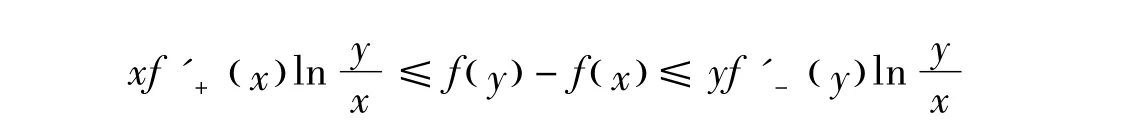
当且仅当f(x)=c+dlnx时等号成立，c、d是常数。

证明 令h(x)=f(ex)，那么

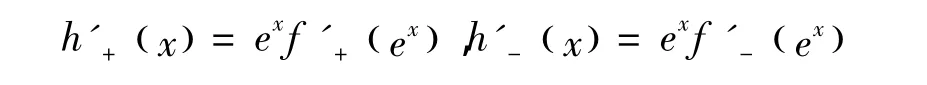
因为 f(x)是［a，b］⊂(0，∞)上的 GA －下凸函数，由引理1知，h(x)是［lna，lnb］上的下凸函数。根据下凸函数的性质知h'－(x)与h'+(x)在(a，b)单调不减，也即 xf'－(x)和xf'+(x)在(a，b)单调不减。又由引理 2 知，对任意 u，v∈［lna，lnb］，有

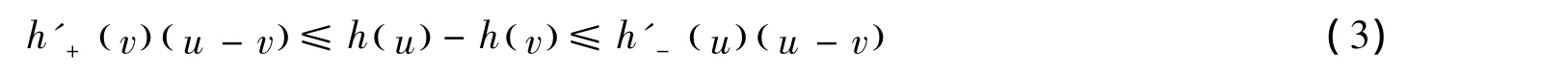
在式(3)中取u=lny，v=lnx，则引理3结论2)得证。

引理4 设f(x)是定义在［a，b］⊂(0，+∞)上的连续的GA－下凸函数，则有

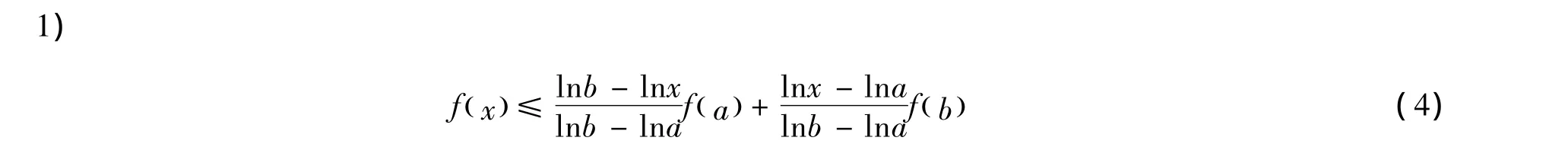
当且仅当f(x)=c+dlnx时等号成立，c、d是常数。

当且仅当f(x)=c+dlnx时等号成立，c、d是常数。

证明 对任意 x∈［a，b］，有

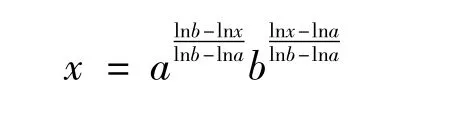
由GA－下凸函数的定义得式(4)。式(4)在［a，b］上取积分得式(5)。

设 f(x)是定义在(a，b)上的可导的下凸函数，对于任意 x1，x2∈［a，b］，x1＜x2，文献［6］证明了下面结果:

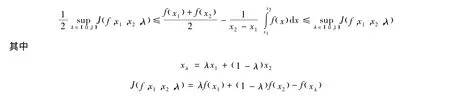
本研究将仿照文献［6］的方法，将上述结果移植到GA－下凸函数。设0＜x1＜x2，λ∈(0，1)，引入记号

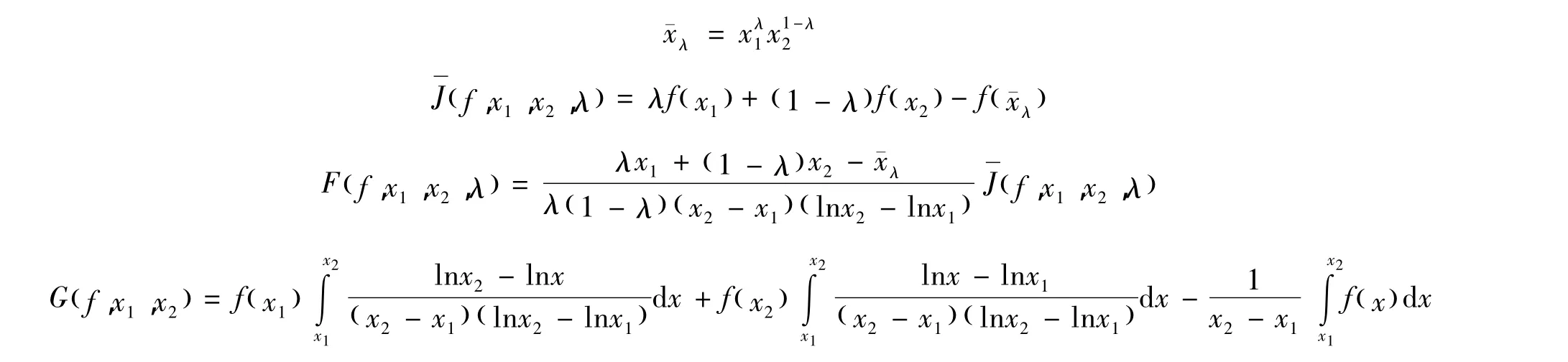
本研究的主要结果:

定理2 设 f(x)是定义在(a，b)上的可导的 GA －下凸函数，对于任意 x1，x2∈(a，b)，x1＜x2，有

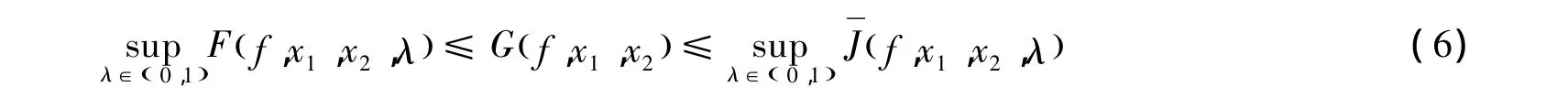
当且仅当f(x)=c+dlnx时等号成立，c、d是常数。

2 定理2的证明

由引理4得

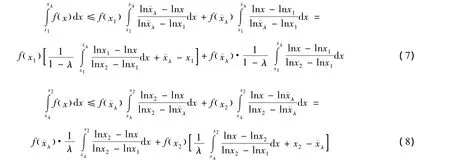
式(7)、(8)两式相加得:

则式(6)的左端部分得证。

由Cauchy中值定理，存在τ∈(x1，x2)，使得

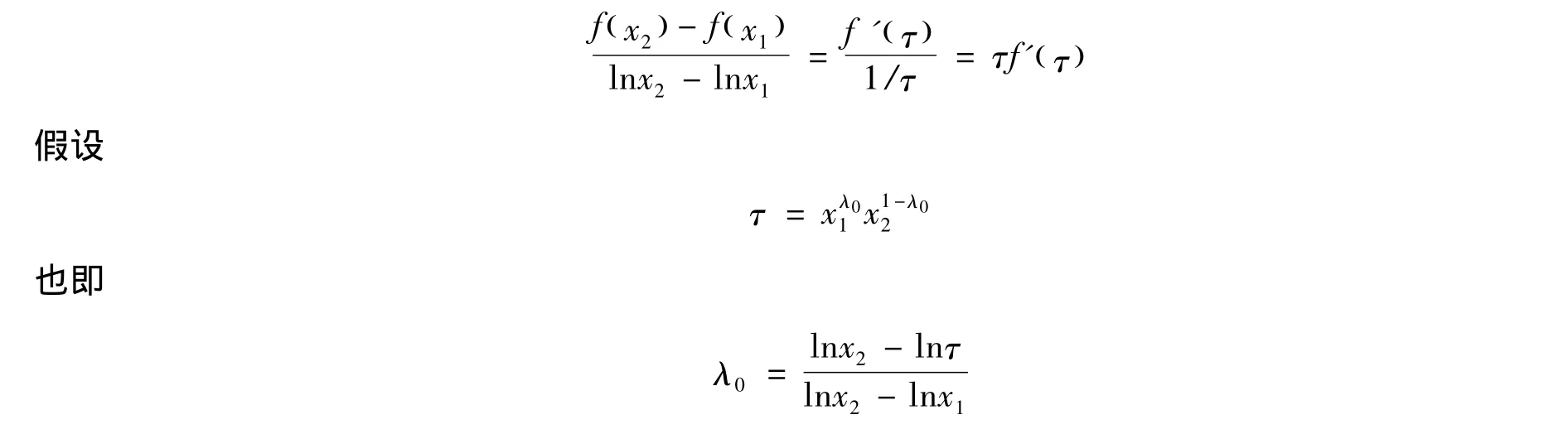
由引理3 知，对于任意 x∈［x1，x2］，有

式(13)的两边对x在［x1，x2］上积分得

式(6)得证。

当f(x)=c+dlnx(c、d是常数)时，经简单计算可知式(6)中的3项都为零，所以等号成立。反之，若式(6)的等号成立，则由上面的证明过程可知，必有式(14)等号成立，由引理4知，f(x)=c+dlnx(c、d是常数)。

推论1 设 f(x)是定义在(a，b)上的可导的 GA －下凸函数，对于任意 x1，x2∈(a，b)，x1＜x2，有

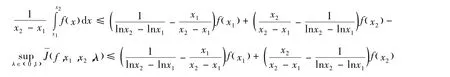
当且仅当f(x)=c+dlnx时等号成立，c、d是常数。

［1］吴善和.GA－凸函数与琴生不等式［J］.贵州师范大学学报:自然科学版 ，2004，22(2):52-55.

［2］ZHANG X M，CHU Y M.A Double Inequality for the Gamma and Psi Functions［J］.International Journal of Modern Mathematics，2008，3(1):23-27.

［3］华云.关于 GA-凸函数的Hadamard型不等式［J］.大学数学，2008，24(2):147-149.

［4］张小明，褚玉明.解析不等式新论［M］.哈尔滨:哈尔滨工业大学出版社，2009:198-203.

［5］匡继昌.常用不等式［M］.3版.济南:山东科学技术出版社，2004:375-376.

［6］Zoran D.Mitrovi.A Remark on Hadamard’s Inequality［J］.Applied Mathematical Sciences，2008，2(43):2127-2130.