具有Holling II类功能反应的3种群食物链模型稳定性

闫 莎

(安康学院 数学系，陕西安康 725000)

讨论3种群食物链模型［1］

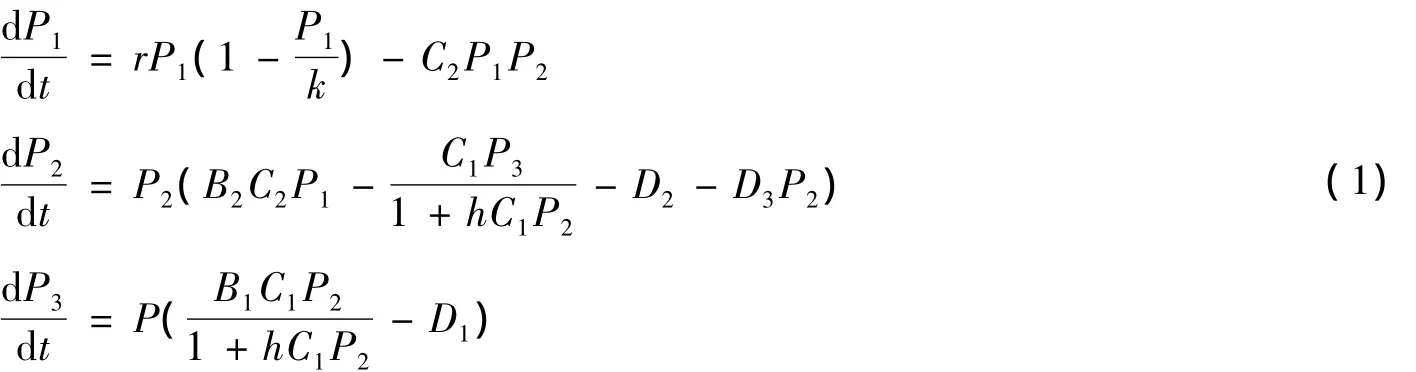
解的一致有界性和正平衡点的稳定性。式(1)中:P1、P2、P3分别表示食饵、捕食者和最高捕食者种群的密度;是Holling II型功能反应函数;P2自身具有密度制约;B1、B2是捕食者P3、P2的转化率;h是捕食者P3的消化系数;D1、D2是捕食者P3、P2的死亡率;D3是捕食者P2的密度制约系数;C1、C2是捕食者P3、P2的捕食率;r和k分别是食饵 N的内禀增长率和环境容纳量。详细的生态意义见文献［1－3］。

本文主要采用文献［4］的思想，应用线性化方法和Lyapunov函数方法讨论模型(2)的正平衡点的稳定性。

1 一致有界性

经简单计算知，式(2)至少有平凡平衡点(0，0，0)和半平凡平衡点(1，0，0);至多有一个正平衡点，其存在的充要条件是

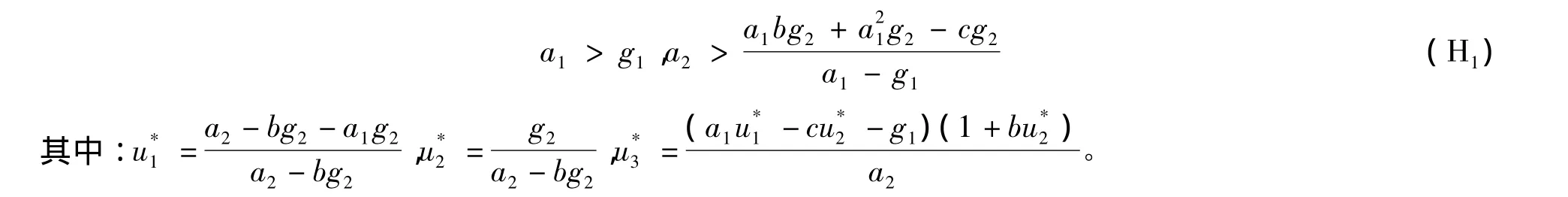
定理1 设(u1(t)，u2(t)，u3(t))是系统(2)取正初值 $(u1(0)，u2(0)，u3(0))时的解，其中［0，T)是解最大存在区间，则存在依赖于式(2)的系数以及初值ui(0)(i=1，2，3)的正常数M，使得0≤ui(t)≤M(i=1，2，3)，进一步有 T=+ ∞。

证明 设(u1(t)，u2(t)，u3(t))是问题(2)在初值 ui(0)≥0(i=1，2，3)时的解，由比较原理［5］易知，当 t∈［0，T)时，(u1(t)，u2(t)，u3(t))≥0。

下面证明(u1(t)，u2(t)，u3(t))在［0，T)上是有界的。对式(2)的第1个方程应用比较原理得

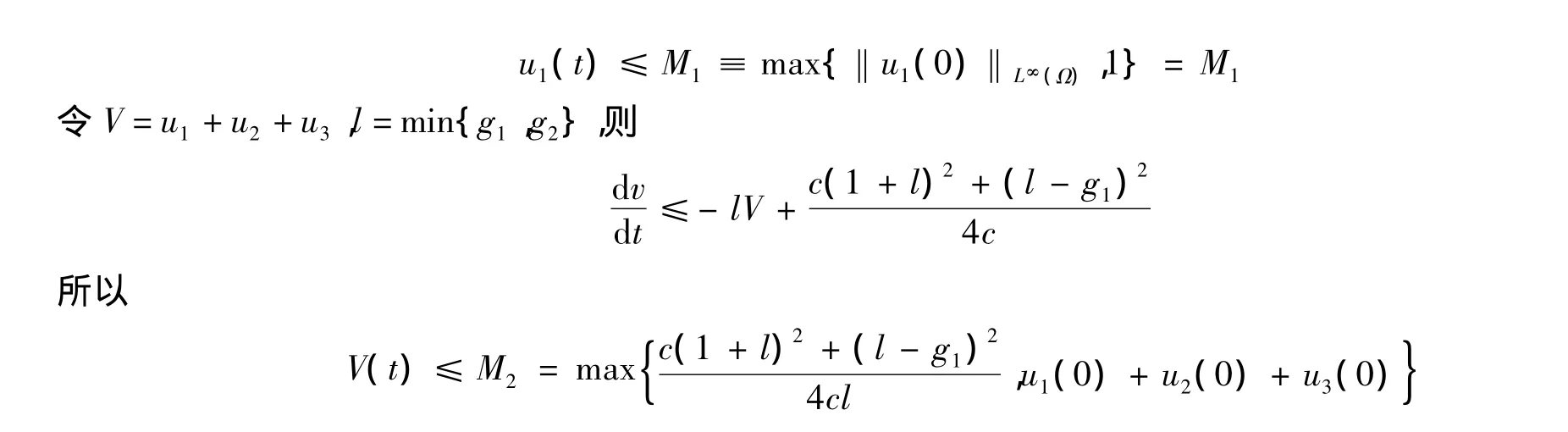
因此，对∀t∈［0，∞)，有 ui(t)≤M(i=1，2，3)。由延拓定理得 T=+∞。

2 局部渐近稳定

系统(2)在E*处的线性化矩阵为

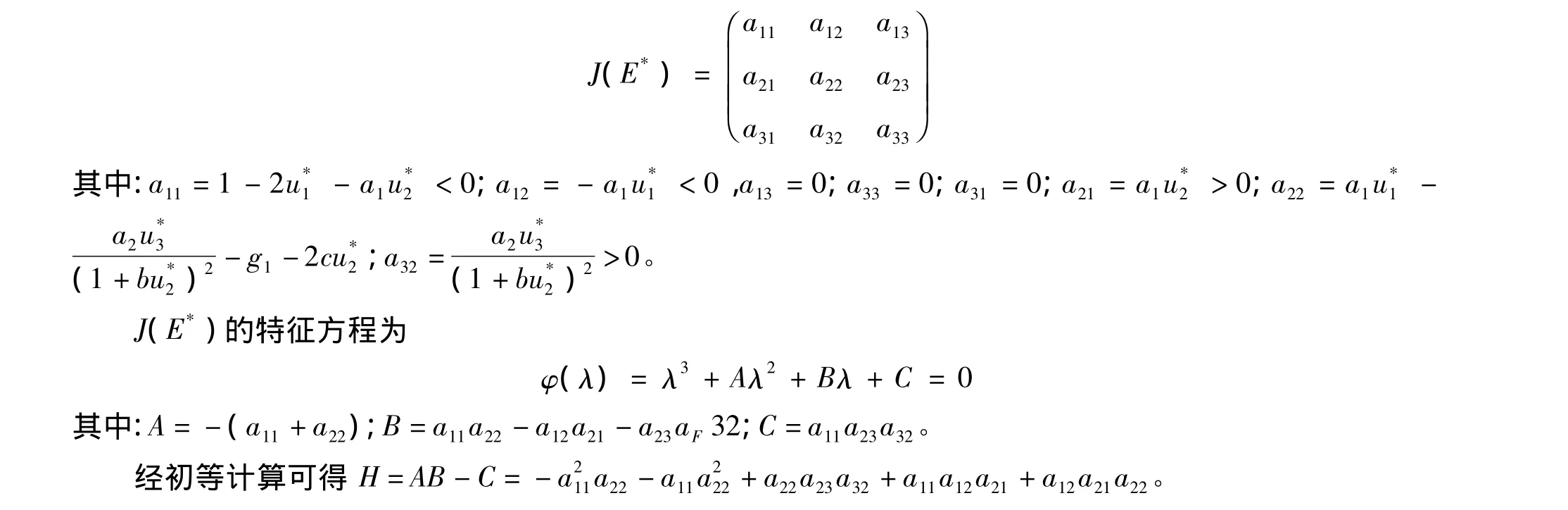
要使 φ(λ)的3 个根 λ1、λ2、λ3均有负实部，必有A ＞0，C ＞0，H ＞0，即 a11、a22均为负。注意到 a11＜0成立，而a22＜0的充要条件是

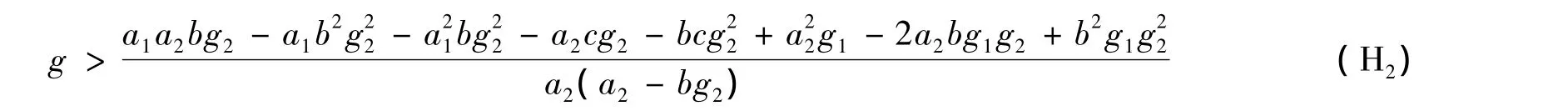
于是，由文献［6］定理5.5.1可得如下结论:

定理2 若条件(H1)、(H2)成立，则问题(2)的正平衡点局部渐近稳定。

3 全局渐近稳定性

由Lyapunov-Lasalle不变原理［7］，再结合E*得局部渐近性，从而可得E*是全局渐近稳定的，即:

定理3 若条件(H1)、(H2)、(H3)成立，则问题(2)的正平衡点E*全局渐近稳定。

［1］Armstrong R A，McGehee R.Competitive exclution［J］.Am Nature，1980，115:151-170.

［2］陈兰荪.数学生态学模型与研究方法［M］.北京:科学出版社，1988.

［3］Abrams A，Brassil E，Holt D.Dynamics and responses to mortality rates of competing predators undergoing predator-prey cycles［J］.Theoretical Population Biology，2003，64:163-176.

［4］Xin-an Zhang，Lansun Chen，Avidan U N.The stage-structured predator-prey model and optimal harvesting policy［J］.Mathematial biosciences，2000，168:201-210.

［5］叶其孝，李正元.反应扩散方程引论［M］.北京:科学出版社，1999.

［6］May R M.Stability and Complexity in Model Ecosystems［M］.［S.l.］:Princeton University Press N J，1974.

［7］Hale J K.Ordinary Differential Equations［M］.［S.l.］:Krieger Malabar F L，1980.