严重噪声污染下的模糊图像复原方法

周 徽

(中国电子科技集团公司第二十八研究所，南京 210007)

数字图像复原/恢复技术(以下简称复原技术)是数字图像处理的重要研究内容，已在诸多领域取得了成功应用［1］。

由于现有的图像系统都存在某种程度的缺陷，呈现出各种退化因素，因而进行图像复原是必要的。总体上退化因素可以归结为2类。①空间退化，又称为模糊。成像系统中某些元件失常、图像传感器与成像目标之间的相对移动、摄像机失焦、不良天气影响等因素都会造成图像模糊。②点退化，通常指噪声。最常见的点退化来自电子元件或数字化噪声。

图像退化过程可被模型化为一个退化函数和一个加性噪声项共同作用于原始图像f(x，y)，从而产生一幅退化的图像g(x，y)，如图1所示。根据该模型，退化图像的数学描述见式(1)。

其中:g(x，y)代表退化图像;f(x，y)代表未退化图像;n(x，y)代表噪声项;h(x，y)代表模糊算子，又称点扩展函数(point spread function，PSF);符号“*”代表卷积。为了便于描述，式(1)改写为矩阵形式

其中:f、g和n为NM×1维向量，由二维图像按行或者列堆积而成;H是由PSF生成的MN×MN块循环矩阵。

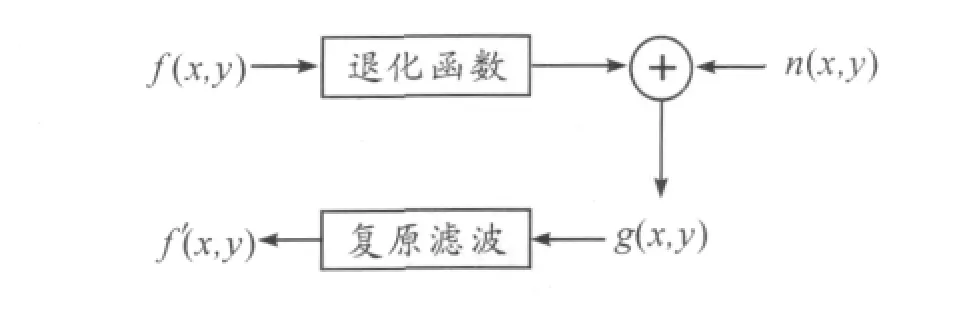
图1 基本图像退化/复原模型

理论上，在给定f(x，y)以及退化函数H和噪声n(x，y)的一些先验知识后，便可以获得原始图像的一个近似估计f^(x，y)。然而，式(2)具有病态特性，导致直接求解不容易实现，只能先设法对式(2)施加一定的约束，将其病态转为良态后再设法求其最优估计解。这个估计应能尽可能接近原始图像。

针对该问题，人们提出过许多方法，如在已知g、H与n有关的先验知识的前提下，去求原图像的逼近解。在这些方法当中，Tikhonov正则化方法最具优势［2］。该方法是一个在L2空间的最小方差近似问题，能够平衡精确性与平滑性［3］，因而得到广泛研究。它将式(2)变为带约束条件的优化解，即

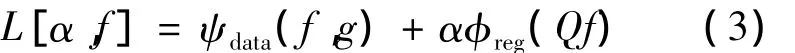
其中:ψdata(f，g)表示数据逼近项;φreg(Qf)表示正则化项;Q为高通滤波算子;d为正则化参数，用以控制数据逼近项与正则化项的空间分布。理论上，在 L(α，f)最小化，即条件下的解就是原图像f(x，y)的最优逼近解。

在正则化方法应用中确定正则化参数是非常关键的一步。人们先后提出过许多关于如何选择正则化参数的方法。Galatsanos等［4］提出了基于均方误差(MSE)评判标准的正则化参数选择和噪声变量估计方法。Nakano等［5］提出用权矩阵的方式优化正则化效果，而局部正则化优化权矩阵从迭代过程获得。Reeves［6］则给出了在限制性条件下，用交叉有效性准则判断正则化最优度的方法。Molina等［7］将等级贝叶斯方法应用到图像复原中，提出了一个3步方法。该方法在每个步骤中完成1个正则参数的确定，降低了对噪声先验知识的依赖性。Leung［8］提出用L曲线作为选取正则化参数的依据，通过实验验证了L曲线的曲率与正则化参数优异性之间的相关性，其结论是:当曲率最大化时，取得的参数是最优的。Demoment［9］综述了正则化方法的详细内容。

上面提到的正则化参数选取方法都具有全局性限制，即参数在算法开始之前就已经确定，导致过分依赖于先验信息，无法在算法迭代过程中自适应修正。与上面的方法不同，Katsaggelos等［10］提出用正则化函数取代全局正则化参数的方法，使算法能够自适应地修改正则化参数，大幅提高了算法的效率。本文的工作就是充分利用该思想，提出一种改进的自适应加权正则化迭代图像复原方法，增强算法对强噪声存在时的适应性。

1 自适应正则化函数

用含有自变量f的正则化函数α(f)代替全局正则化参数α，建立目标平滑泛函式(4)。

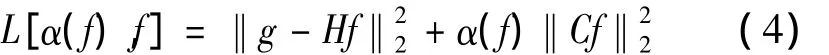
目标泛函建立之后，正则化参数的选择至关重要。自适应正则化函数α(f)的选取应满足3条性质［10］:① α(f)为平滑泛函的函数;② α(f)与目标泛函之间需满足一定的极值性质，即当时，α(f)→0;‖g － Hf‖时，α(f)→∞;③ 在α(f)取值范围内不改变目标泛函的凸函数性质。

根据上面性质，假设存在正实数λ使得式(5)成立，则

正则化项用于惩罚解的粗糙性，然而过分的惩罚会造成解的过分平滑，抑制算法对高频成分的恢复，从而导致复原结果在图像强度变化剧烈处产生振铃效应，影响图像视觉效果。因此，在复原滤波时，必须将图像局部细节特性考虑在内，采取加权形式增强算法的局部适应能力，提高算法对振铃的抑制能力，改善复原质量［5］。

文献［11］认为，图像中小的梯度值对应噪声，需对其进行平滑，而大的梯度值则对应图像边缘轮廓，应给予保护。根据该理论，定义加权正则化项为

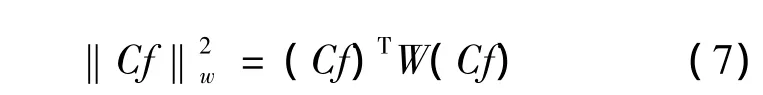
其中W是由wij构成的矩阵，wij定义为

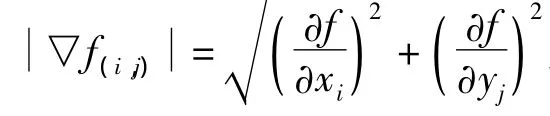
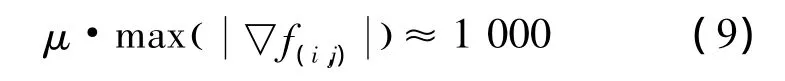
加权后的自适应正则化函数如式(10)所示。

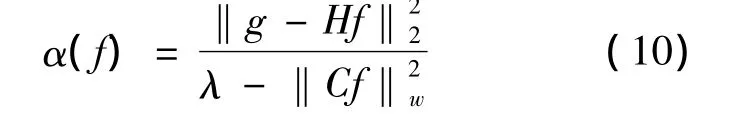
2 迭代复原算法及收敛性分析

图像复原过程等价于式(4)定义的平滑函数逼近最优解的过程。由于目标泛函的凸性，恰当地选取正则化参数能够使式(4)存在唯一的全局最优解。该最优解在平滑函数梯度为0时取得，即

将式(11)对f求导，得

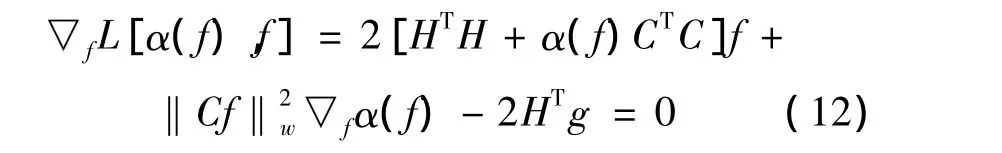
因为α(fk)是第k次迭代结束后计算出的参数，用于第k+1次迭代，所以▽fα(f)=0，从而式(12)化简为

建立逐步逼近的Van Cittert格式的迭代等式:

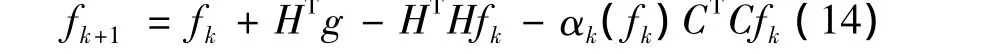
首先分析算法的收敛性，改写式(14)为

对式(15)左右两边同时取范数，并根据矩阵范数与向量范数的协调性，有

反复使用这个不等式得

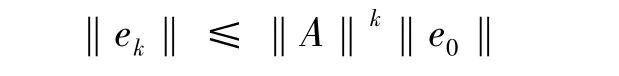
下面分析算法的收敛条件。因为‖A‖＜1等价于 ρ(A)＜ 1，有

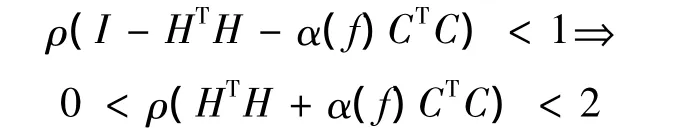
其中ρ(·)定义为“·”的谱半径。根据三角不等式，上式等价于

通过规范化H、C可使ρ(HTH)和ρ(CTC)均不大于1，从而算法收敛的充分条件演变为α(f)＜1，即

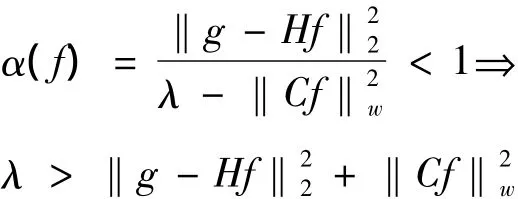
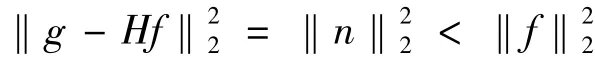
算法流程描述:

步骤1 设置初始值f0=g，迭代计数值k=0，设定算法终止条件ε=10－7，开定时器。

步骤2 在第k步迭代中，自动修正正则化参数αk(fk)，并利用式(14)对图像进行复原滤波。更新fk+1。

步骤4 关定时器，计算复原评价指标ISNR，显示复原结果。

3 实验与分析

选择2组实验验证本文提出算法的有效性。第1组是样条图像，用来验证算法对图像边缘恢复的效果;第2组是经典的lena图像，用来验证算法对图像细节恢复的效果。

实验1 样条图像尺寸为158×300的灰度图像，如图2(a)所示。本实验在PC机(CPU为P42.4GHz，内存512 Mbytes)上进行，模糊算子H取为11×11的均匀模糊，随机叠加信噪比为20 dB的高斯噪声，C取2－D拉普拉斯算子。判据‖fk+1－fk‖/‖fk‖ ＜10－7作为算法终止迭代的条件，改进信噪比(improvement signal-to-noise ratio，ISNR)作为算法性能的评价指标，ISNR定义为

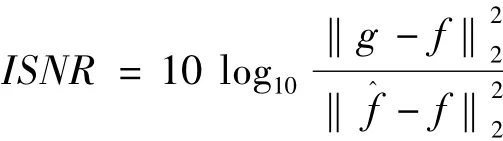
图2 样条图像复原效果

图2(a)、(c)、(e)分别为原始样条图像、退化图像和复原图像。图2(b)、(d)、(f)分别为穿越图2(a)、(c)、(e)中部的水平扫描线，其横坐标为水平象素点，纵坐标为对应象素的亮度值。

由图2(e)可以看出，相对于图2(c)，算法恢复的视觉效果是比较理想的。图2(f)给出的复原图像中部的扫描线说明样条交接的轮廓线基本得以复原，显然较图2(d)有明显改善。实验获得的具体参数见表1和图4。

实验2 lena图像尺寸为300×300的灰度图像，如图3所示。其他条件同实验1。图3(a)、(b)分别为退化的lena图像和复原后的lena图像。图3(c)、(d)分别为图3(a)、(b)的局部放大图像。实验获得的具体参数见表1和图4。

图3 lena图像恢复效果

表1 实验结果参数

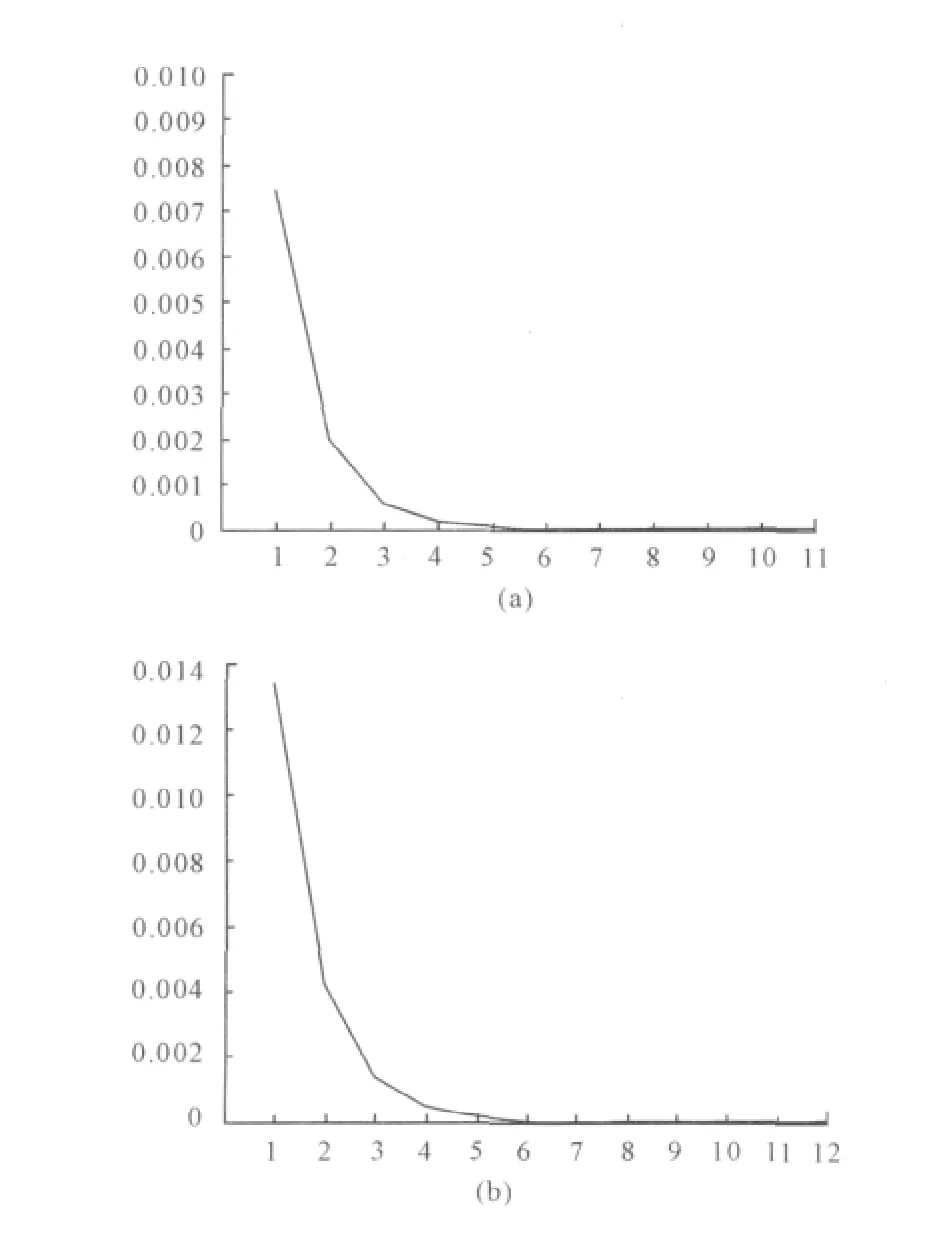
图4 收敛误差曲线

图4给出2组实验中每一迭代步骤对应的误差判据变化曲线，其中图4(a)是样条图像，图4(b)是lena图像，横坐标对应迭代次数，纵坐标对应误差判据值。由图4可以看出，无论迭代初始条件如何，算法能够以较少的迭代次数快速平稳地趋向于最优估计解。

4 结束语

本文提出一种改进的自适应加权正则化迭代图像复原算法。该算法能够自适应地选择并自动修正正则化参数。算法对初始值不敏感，在每步迭代中，算法完成1次复原滤波，并更新正则化参数，确保结果能够快速趋向于最优。讨论了算法的收敛性与收敛条件，通过建立显式迭代复原算法寻找全局最优解。该算法具有占用内存小、计算速度快等优点。无需任何噪声信息作为先验知识，算法通过观测图像本身自适应估计并调整正则化参数以适应强噪声存在下的复原操作。用2组实验验证了算法的有效性。结果显示:该算法能提高算法对强噪声存在的适应性，抑制Gibbs振铃波纹，具有较好的评价结果和较高的实时性。

［1］Banham M R，Katsaggelos A K.Digital image restoration［J］.Signal Processing，1997，14(2):24-41.

［2］Bouhamid A，Jbilou K.Sylvester Tikhonov-regularization methods in image restoration［J］.Journal of Computational and Applied Mathematics，2007，206(1):86-98.

［3］Leung C M，Lu W S.Optimal determination of regularization parameters and the stabilizing operator［J］.Signal Processing，1995，201:403-406.

［4］Galatsanos N P，Katsaggelos A K.Methods for choosing the regularization parameter and estimating the noise variance in image restoration and their relation［J］.IEEE Transactions on Image Processing，1992，1(3):322-336.

［5］Nakano K，Eguchi M，Toyota Y，et al.On regularization for image restoration problems from the viewpoint of a Bayesian information criterion ［C］//IECON-93.Hawaiian，USA:［s.n.］，1993:2257-2261.

［6］Reeves S J.Optimal regularized image restoration with constraints［C］//ICASSP-92.San Francisco，USA:［s.n.］，1992:301-304.

［7］Molina R，Katsaggelos A K，Mateos J.Bayesian and regularization methods for hyperparameter estimation in image restoration.Image Processing［J］.IEEE Transactions on Image Processing，1999，8(2):231-246.

［8］Leung C M，Lu W S.An L-curve approach to optimal determination of regularization parameter in image restoration.Electrical and Computer Engineering［J］.Electrical and Computer Engineering，1993，2:1021-1024.

［9］Demoment G.Image reconstruction and restoration:overview of common estimation structures and problems［J］.IEEE Transactions on Signal Processing，1989，37(12):2024-2036.

［10］Moon G K，Katsaggelos A K.General choice of the regularization functional in regularized image restoration［J］.IEEE Transactions on Image Processing，1995，4(5):594-602.

［11］Charbonnier N P，Blanc F L.Deterministic edge-preserving regularization in computed imaging［J］.IEEE Transactions on Image Processing，1997，6(2):298-311.