有限群的阶与群的结构*
夏 晶
(大庆师范学院)
0 引言
通过群的阶来给出群的一些性质已有许多结果.例如著名的Feit-Thompson定理:奇数阶群必可解和Burnside定理:设p、q是素数,a、b是正整数,则paqb阶群必可解等等.以及在文献[1]中还给出了象有限p-群(p是素数)是幂零群阶是2n,n是奇数的群是可解群,p2(p是素数)阶,群必为交换群等重要结果.该文给出了若群的阶|G|=p1p2…pn,则G是超可解群;以及群G的阶|G|=60p1…pn,若G是极小单群,则G≌A5,这里p1,p2,…,pn是互不相同的大于5素数.
1 主要概念和引理
定义 极小非可解群即每个真子群为可解的单群,称之为极小单群.
引理1[1]设p是群G的阶的最小素因子,P∈Sylp(G),P循环,则G有正规p-补.
引理2[1]设G是非交换单群,p是G的阶的最小素因子,则p3||G|或12||G|.
引理3[1]60阶单群必同构于A5.
引理4[2]极小单群有下述五个类型:
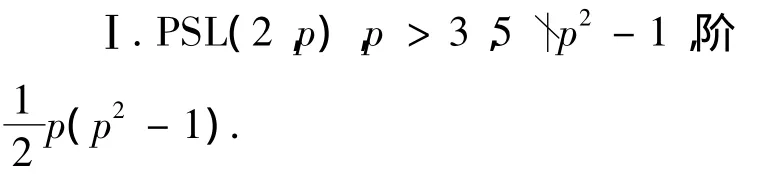
Ⅱ.PSL(2,2q),q是素数,阶 2q(22q-1)
Ⅲ.PSL(2,3q),q是奇素数,阶·3q(32p-1).
Ⅳ.PSL(3,3),33(33-1)(32-1)=24×33×13.
Ⅴ.Suzuki群S2(2q),q奇素数,阶(22q+1)22q(2q-1).
引理5[1]60阶单群必同构于A5.
2 主要定理
定理1 设G的阶为|G|=p1p2…pn,其中p1,p2,…,pn是不同的素数,则G是超可解群.
证明 不妨设p1<p2<…<pn.当n=1时,G是p-群,是幂零群,当然是超可解群.于是可以假设n≥2,Sylow定理知G的Sylowp1-子群P1的阶是素数p1,从而是循环子群.于是G有正规p1-补G1,且|G1|=p2…pn.同理G1有正规p2-补G2.即G2◁G1,且|G2|=p3…pn.易知G2是G的Hall子群,再由G2是G的次正规子群,从而G2是G的正规子群.如此下去,我们得到G的一个正规子群列.
使得|Gi-1/Gi|=pi,i=1,2,…,n.从而G是超可解群.
定理2A5是极小单群.
证明 设N是A5的任意真子群,由|A5|=60,|M|||A|知|N|=1,2,3,5,4=2×2,6=2×3,10=2×5,12=22×3,15=3×5,20=22×5,30=2×3×5,即|N|=p,paq,pqr型群.其中p、q、r是不同的素数,由文献[1]及定理1,知N是可解群.而A5是单群,从而A5是极小单群.
定理3 设群G的阶为|G|=22×3×5×p1×p2×…×pn,其中p1,…,pn均是大于5的不同素数,若G是极小单群,则G≌A5.即G是阶为60的单群.
证明 由引理4知G只有五个类型的可能.若G是类型Ⅰ由5||G|,5,知p=5.即

由引理5知G≌PSL(2.5)≌A5.
若G是类型Ⅱ.由22|||G|,及q是素数知,q=2,即22(22×2-1)=60.从而有G≌A5≌PSL(2.4).
若G是类型Ⅲ,q是奇素数,则33||G|,与|G|恰好被3 整除,矛盾,故G≌/PSL(2,33).
由24||PSL(3,3)|,知G≌/PSL(3,3),即G不可能是类型Ⅳ.
若G≌S2(2q).由q是奇素数知26||G|,与4|||G|矛盾.故G≌/S2(2q).
综上所述,有G≌A5.
[1] 徐明曜.有限群导引(上)[M].北京:科学出版社,1999.
[2] 陈重穆.内外-∑群与极小非-∑群[M].重庆:西南师范大学出版社,1988.

