双币种模型下资产价格带跳的欧式期权定价*
高惠泽,王玉文
(哈尔滨师范大学)
0 引言
现代期权定价理论始于1973年,由美国芝加哥大学教授Black与Scholes发表了“The Pricing of Options and Corporate Liabilities”一文,导出了著名的Black-Scholes期权定价公式,但是该模型假设股票的价格服从几何布朗运动,即股票价格是连续的,而市场中股价往往是不连续的,经常会出现股价“跳空”的现象.因此,众多学者就提出了各种期权定价模型,如 John C.COX 和 Stephen A.ROSS 引入纯跳跃的模型[3].另一方面,在金融市场中,经常利用期权来对冲已有的风险,这种对冲不仅局限在国内的单一市场,在国际市场中也经常发生,此时,单一的货币模型已经不再适用.笔者受文献[1,3]启发,将文献[2]中的双币种模型推广至带跳的情形,选取英镑和美元市场为例,假定以英镑计价的风险资产价格是跳跃的,跳跃幅度为常数且跳跃服从Possion过程.
1 带跳的双重货币模型
记{Bt}t≥0和{Dt}t≥0分别为美元和英镑现金债券,记Et为t时刻1英镑的美元价值和St为t时刻的英镑风险资产价格,则模型为

定义1[1]一个金融资产称为双重货币工具,如果它是以另一种货币作为清算的衍生证券.
引理1[1](多因子 Girsanov定理)设在生成σ-域流的测度P下…,n,是独立的布朗运动,令…,n为可料过程,使得

引理2[1](资产价格带跳的 Girsanov定理)设是一个标准的P-布朗运动,是在P下强度为的(可能是时间非齐次)泊松过程,即是一个P-鞅.记为由生成的σ-域,假设和是可料过程,且对每一个t,φt为正,使得和<∞,那么在测度Q下,它关于P的Radon-Nikodym导数为,这里L0=1.且,定义为的过程是个布朗运动且的强度为
2 双重货币模型下资产价格带跳的欧式期权定价
假定市场是无套利的(否则不存在等价鞅测度),利用上述两个引理构造等价鞅测度Q,找到Q关于P的Radon-Nikodym导数中的θi,i=1,2和φt,使得在测度Q下资产的贴现价格是鞅,从而利用鞅方法进行定价.
由于模型中风险资产的价格是以英镑计价的,英镑资产在美元市场不可交易,但是英镑债券的美元价值EtDt以及风险资产的美元价值EtSt在美元市场中是可交易的,选取美元现金债券作为计价单位.
定理1 双重货币模型中带跳风险资产敲定价格为K到期日为T的欧式看涨期权在t时刻的价格Vt为

其中

证明 分为两部分,(a)要构造测度Q,(b)要计算在测度Q下资产贴现收益的期望.
(a)因为EtDt和EtSt为美元可交易资产,由期权定价的鞅方法,需要构造等价鞅测度Q,使得资产价格的贴现值在测度Q下是鞅,进而求得此权益在Q测度下的贴现收益的期望.
首先求出Yt与Zt满足的随机微分方程


利用多因子分部积分公式,得
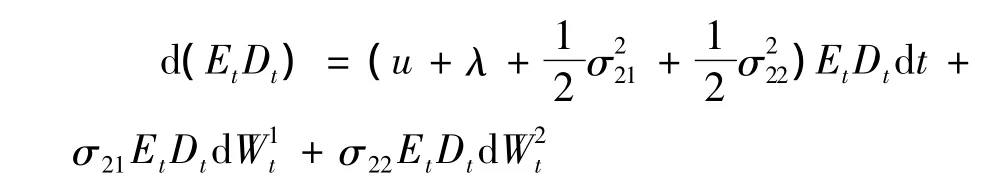
因此

如果资产价格存在跳,投资者期望补偿与跳跃有关的附加风险(即存在“补偿的”跳跃),此时,由风险资产价格跳跃而引起的附加风险为E[ηλtν],其中,ν是资产价格对市场震动的敏感性测度,η表示每单位带跳的风险资产的高额回报率.由引理2中Mt及“补偿者”Λt的定义,用dMt代替dNt,使风险资产跳跃的附加风险得到补偿,使得由风险资产跳跃产生的附加风险被抵消,这样的风险资产价格满足:
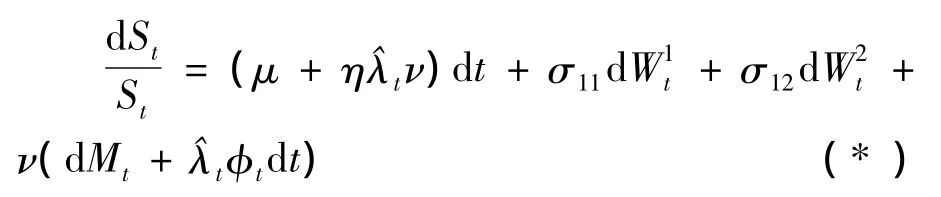
利用Itô公式,重复上面的方法,可得Zt满足的随机微分方程
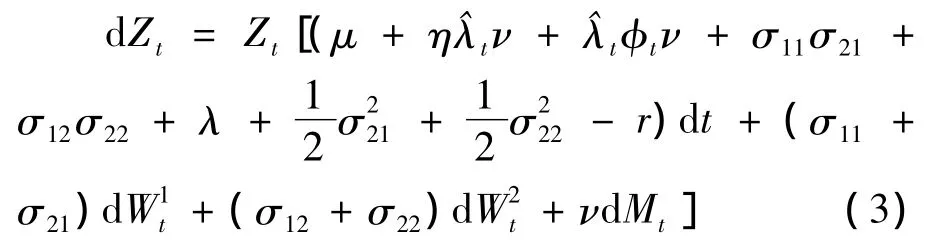
此时由引理2,在测度Q下i=1,2和已经为鞅.由引理1,若要满足资产的贴现值在测度Q下为鞅,则需(2)、(3)中的漂移项为0,因此有

解方程组(4)得:

为保证Yt、Zt在测度Q下是鞅,而非局部鞅,还需要满足如下的 Novikov条件[1]:
注2 此时,由于φ=-η,对 式两端取期望,得

(b)在方程(1)中如果存在一个震荡,那么资产的价格将以因子(1+ν)减少,因此,在测度Q下,方程(1)的解为

进而,令τ=T-t,得

那么在测度Q下,由前面的计算知此欧式看涨期权的价格为

在测度Q与Ft条件下与是独立同分布的布朗运动,都服从均值为0方差为τ的正态分布,即,因此,由正态变量和的分布,有

而ST>K⇒z>

其中z为标准正态随机变量,做变换由正态分布的对称性,知
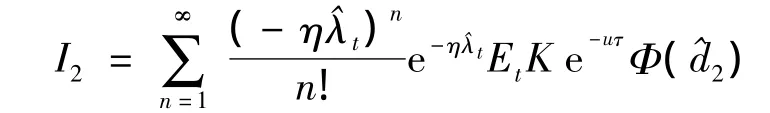


注3 在此定理中,如果令σ11=σ1,σ12=0,σ21=ρσ2,σ22,,即得文献[1]中双重货币模型.
[1] 埃瑟里奇.张寄洲译.金融数学教程[M].北京:人民邮电出版社,2006.
[2] 约翰·赫尔.王勇,索吾林,译.期权、期货及其他衍生产品:第七版[M].北京:机械工业出版社,2009.
[3] Cox J C,Ross S A.The valuation of options for alternative stochastic processes[J].J Fina Eco,1976,3(1):145-166.
[4] 王莉,杜雪樵.跳扩散模型下的欧式障碍期权的定价[J].经济数学,2008,25(3):248-253.

