局部凸空间中的集合极小元的刻画*

刘 齐 ，胡艳红，马玉秋

(1.哈尔滨师范大学;2.哈尔滨学院)

向量优化理论是优化理论和应用的主要研究领域之一.对这一问题的研究涉及到凸分析、非线性分析 、非光滑分析 、偏序理论等多门学科.它的理论和方法在现代社会经济中具有十分广泛的应用，因此向量优化理论的研究既具有重要的理论价值也具有实际应用意义.Phelps在文献［1］中，定义了一个Bishop-Phelps锥，在Phelps文献［1］和Jahn文献［2］中，证明了任何一个有有界闭基的尖锥，都存在包含 C的Bishop-Phelps锥.2001年，Gasimov在文献［3］中证明了由Bishop-Phelps锥引入偏序的赋范空间中，在没有凸性和有界性的假设下，一类单调增的次线性函数支撑点集就是Benson意义下的真有效点集.

在文献［4］中Refail Kasimbeyli给出了3种扩展对偶锥的定义.由这些扩展对偶锥的元素定义了一族特殊的单调增次线性函数.作为锥分离的应用，Refail Kasimbeyli利用纯量化技巧，证明了Banach空间中集合的真有效点都可以由最小化某个次线性函数来计算.

该文主要是在上述文献的启发下，在局部凸空间下，将一般对偶锥推广，并用扩展对偶锥的元素定义了一类单调增的次线性函数.给出了扩展对偶锥的一些性质和利用一个对非凸向量优化问题的简单有效的纯量技巧，并由此证明集合的有效点解可以通过计算某个次线性泛函的最小点得到.在赋范空间中Phelps定义的Bishop-Phelps锥如下:

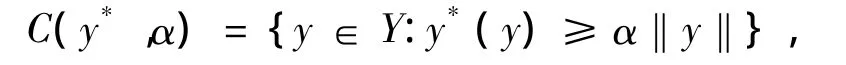
其中α∈(0，1］，y*∈Y*是一个连续的线性泛函且‖y*‖ =1.锥可以被表示成这个函数f(y)=α‖y‖-y*(y)的零次水平集.

设Y是一个实的拓扑向量空间，Spec(Y)是Y上的一族半范，则可由Spec(Y)引入局部凸的拓扑，使得Y是局部凸的拓扑向量空间.

令C是Y的非空子集，集合C是一个锥是指:若y∈C，λ ≥0，λy∈C.

一个锥C是尖的是指:C∩(-C)={0}.

一个锥C是生成锥是指:C-C=Y.

由一个集合A生成的锥记为 cone(A):cone(A)={λa:λ ≥0，a∈A}.

一个凸锥C≠{0}的非空凸子集D称为锥C的基是指:

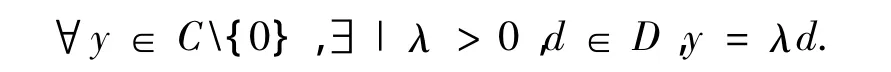
定义1 设Y是局部凸的拓扑向量空间，C是Y中凸锥并诱导一个偏序，

Y的对偶空间记为Y*，C的对偶锥为C*，定义如下:

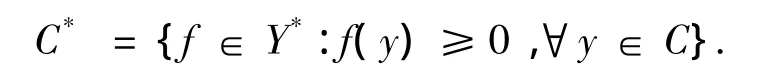
用C#表示C*的拟内部，这里

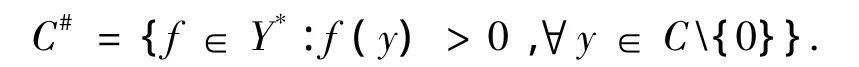
定义2 设Y是局部凸拓扑向量空间，对于存在的f∈Y*任意的p∈Spec(Y)，常数α＞0，定义Bishop-Phelps锥:

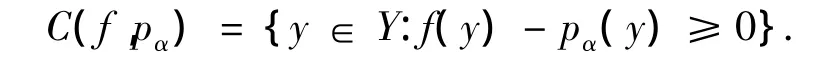
由文献［5］中的定理1.33及推论知，当Y是局部凸空间时，C有一个有界基的充要条件是存在一个非零的连续泛函f满足对任意的连续性半范P，存在一个αp＞0使得f(y)≥αpp(y)，∀y∈C，因此当C具有有界基时，存在一个包含C的Bishop-Phelps锥.

据此引入扩展对偶锥定义如下:

显然有如下的包含关系成立:Ca#⊂Ca0⊂Ca*.

扩展对偶锥的一些性质.

定理1 令C和K是Y中的两个非空锥，假设Ca*非空，则下列结论成立:

(1)若C⊂K，则有Ka*⊂Ca*.(2)对任意的(f，pα)∈Ca*，定义水平集

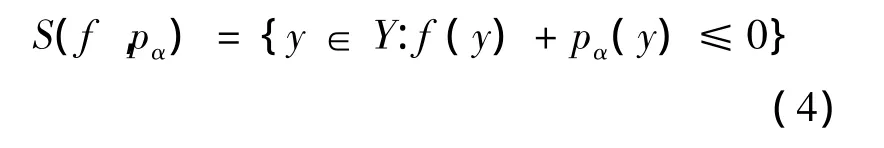
则S(f，pα)是包含-C的闭凸锥.

(3)对任意的(f，pα1)，(f，pα2)∈Ca*若任意的 ∀y∈Y，都有pα1(y)≤pα2(y)，则S(f，pα1)⊂S(f，pα2)成立.

证明 (1)∀(f，pα)∈Ka*，∀y∈K，都有f(y)-pα(y)≥0，对任意的∈C⊂K由于C⊂K.即(f，pα)∈Cα*，故有Kα*⊂Cα*

(2)任取(f，pα)∈Cα*，因为函数g(f，pα)=f(y)+pα(y)是一个连续的正齐次凸函数，故S(f，pα)是闭凸锥.对 ∀y∈-C，有f(-y)-pα(y)≥0即有f(y)+pα(y)≤0，故有-C⊂S(f，pα).

(3)任取(f，pα1)，(f，pα2)∈Cα*，任取(f，pα2).由pα1(y)≤pα2(y)，则 0 ≥f(y)+pα2(y)≥f(y)+pα1(y)，这就说明y∈S(f，pα1)，故有Kα*⊂Cα*.

定义3 令C是局部凸空间Y中的凸锥，函数g:Y→R在Y上是单调的是指:∀y1，y2∈Y，若y1-y2∈C，则g(y1)≥g(y2).

定义4 令C是局部凸空间Y中的凸锥，函数g:Y→R在Y上是强单调的是指:对任意∀y1，y2∈Y，若∀y1-y2∈C{0}，则g(y1)＞g(y2).

定义5 令C是局部凸空间Y中的凸锥，且int(C)非空，函数g:Y→R在Y上是严格单调的是指:对任意y1，y2∈Y，若y1-y2∈int(C)则g(y1)＞g(y2).

定理2 设Y是由一个闭凸锥C赋偏序的局部凸空间 ，任取f∈C#和pα1∈Spec(Y)，定义函数g:Y→R+如下:

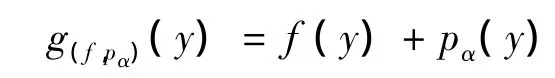
则这个函数g(f，pα)(y)在Y上是单调的，严格单调的若int(C)非空和强单调的当且仅当(f，pα)分别属于Cα*，Cao和Ca#.

证明 充分性:任取y1，y2∈Y，且y1-y2∈C.

任取(f，pα)∈Ca*.

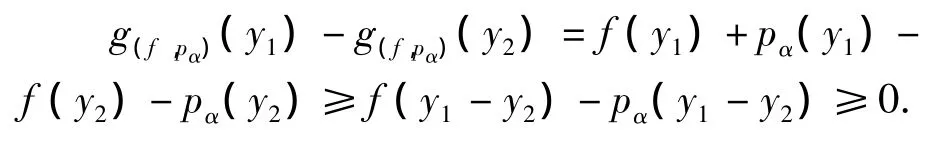
从Cα*的定义中可知g(f，pα)是单调，同理从Cao和Cα#的定义可知g(f，pα)是严格单调和强单调的.

必要性:任取(f，pα)∈C#×Spec(Y)，若g(f，pα)(y)=f(y)+pα(y)是单调的，∀y∈C，0-(-y)∈C.故有0=f(-y)+pα(-y)，即f(y)-pα(y)≥0.从而(f，pα)∈Ca*.当g是强单调和严格单调时也可以分别证明(f，pα)∈Cao，(f，pα)∈Ca#.

定理3 令C是局部凸空间Y的一个闭凸尖锥.若C有一个有界闭基，则C#是非空的.进一步地对于每一个f∈C#，存在Pα∈Spec(Y)满足(f，pα)∈Ca#.

证明 令D为C的一个有界闭基.因为D是闭凸的和0∉cl(D)，知存在一个非零的连续线性泛函f∈Y*和一个实数δ满足

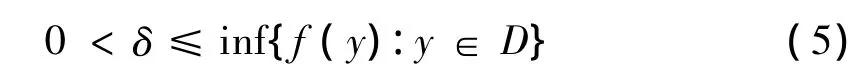
这说明f∈C#，则C#是非空的.

另一方面，对于∀y∈D，令显然pα是连续的半范.

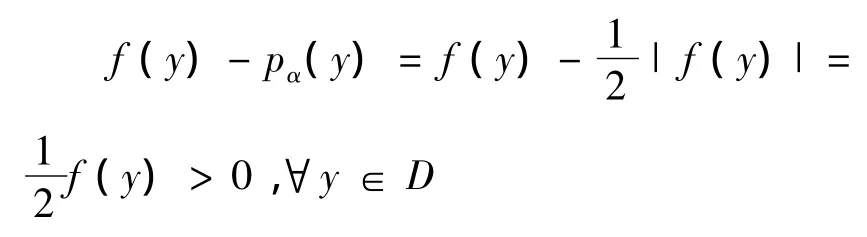
进而f(y)-pα(y)＞0，∀y∈C{0}.这说明(f，pα)∈Ca#.

接下来的定理说明的是 cone(-C)可以表示成(4)中定义的水平集的交集.

定理4 令C是一个实的局部凸空间Y的闭凸尖锥，若C有一个有界闭基，则-C=S(C)，其中

证明 由定理3知C#是非空的.进一步地对于每一个f∈C#，存在Pα∈Spec(Y)满足(f，pα)∈Cα#.再由定理 1 的 (2)知-C⊂S(C).因此，只需去证明相反的结论.假设0≠∈S(C)且∉(-C).令T=R+{}，则T∩(-C)={0}.由于C是闭凸尖锥，那么由文献［6］的定理3.22知存在一个f∈C#使得f)＞0，这样由定理3知，存在Pα∈Spec(Y)满足(f，pα)∈Ca#.由于pα()≥0，有f()+pα()＞0，这与∈S(C)矛盾.

下面的定理可以写成定理4的函数表示.定理5 令C是实的局部凸空间Y的闭凸尖锥.定义函数gC:Y→R如下:

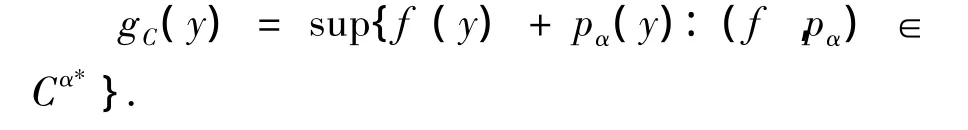
若C有一个有界闭基，则-C={y∈Y:gC(y)≤0}.由定理4的结果直接得到，故略去证明.

令Y是由一个凸锥C⊂Y赋偏序的局部凸向量空间，A是Y中的非空子集.

定义6(a)元素∈A称为集合A的极小元，如果({}-C)∩A}={}

(b)令int(C)非空，元素∈A，称为集合A的弱极小元，如果

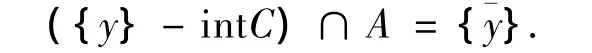
(c)元素∈A，称为集合A有Benson意义下的极小元，如果是A的极小元素或者Y中的零元是A+C在处的射线锥R(A+C，)的极小元，其中R(A+C，)=cl(cone()).

(d)元素∈A，称为集合A有Henig的意义下的真极小元，如果∈A是集合A关于某个凸锥K的极小元，其中C{0}⊂int(K).

定理6 令Y是由闭凸尖锥C⊂Y赋偏序的局部凸向量空间，令

(f，pα)∈Y*×Spec(Y)，Sol(SP)是纯量问题(SP)的最优解集

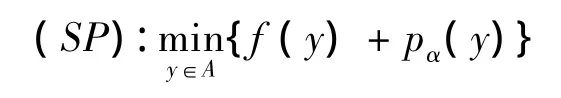
对于一个任何给定的(f，pα)∈Ca*，如果Sol(SP)非空，则下列结论成立:

(1)若(f，pα)∈Cao，则每一个 Sol(SP)的元素都是A的弱极小元素.

(2)若(f，pα)∈Ca*，Sol(SP)是一个单点集，则这个元素是A的极小元素.

(3)若(f，pα)∈Cα#，则 Sol(SP)中的每一个元素都是A有Benson意义下的真极小元.

证明 (1)令(f，pα)∈Cao，用反证法，假设存在∈Sol(P)但不是A的弱极小元.则存在y∈A{}，使得y∈{}-int(C).由(f，pα)∈Cao，由定理2 知函数g(f，pα)=f(y)+pα(y)是严格单调的，进而有g(f，pα)(y)＜g(f，pα)()这与∈Sol(P)矛盾.

(2)令(f，pα)∈Ca*，假设存在∈Sol(P)不是A的极小元素，则({}-C)∩A≠{}，即∃y∈A，使得y∈{}-C，因为(f，pα)∈Ca*.由定理 2 知g(f，pα)=f(y)+pα(y)是单调的，进而有g(f，pα)(y)≤g(f，pα)().这与是Sol(SP)的唯一解矛盾.

(3)令(f，pα)∈Ca#，假设∈Sol(P)不是A有Benson意义下的真极小元.若不是A的极小元素，则({}-C)∩A≠{}}，即∃y∈A，使得y∈{}-C.因为(f，pα)∈Ca#由定理2知g(f，pα)=f(y)+pα(y)是强单调的，进而有g(f，pα)(y)≤g(f，pα)().这与∈Sol(P)矛盾.若0不是射线锥R(A+C，)的极小元素.即cl(cone())∩(-C)≠{0}.存在0≠y1∈-C，使得y1∈，∃y2∈A，y3∈C，使得y1=y2+y3-，y2-1-y3.由(f，pα)∈Ca#，知g(f，pα)=f(y)+pα(y)是强 单调的，g(f，pα)(y)＜g(f，pα)()这与∈Sol(p)矛盾.

［1］ Phelps R R.Support cones in Banach space and their applications.Advances in Math，1974，13:1-19 .

［2］ Jahn J.A generalization of a theorem of Arrow ，Barankin，and Blackwell，SiamI J.Control Optim，1998，26:999-1005.

［3］ Gasimov R N.Characterization of the Benson proper efficiency and scalarization in non-convex vector optimization，in Multiple Criteria Decision Making in the New Millennium(Ankara，2000).Lecture，2006:521-540.

［4］ Refail Kasimbeyli.A nonlinear cone separation theorem and scalarization in non-convex vector optimization.Siam J Optim，2010，20(3):1591-1619.

［5］ Song W，Sach P H.Set-valued Vector Optimization.

［6］ Jahn J.Vector optimization.Springer-Verlin，Berlin，Heidelberg，2004.