Banach空间中分离优化问题的最优性条件分析*

王茜茜

(哈尔滨师范大学)

0 引言

近几十年中，约束集具有分离结构的优化问题受到广泛的关注，因为此类优化问题在数学经济，均衡问题，决策分析等许多实际方面有广泛的应用背景.分离优化是指约束集具有分离结构的优化问题，其中分离结构是指约束集是由有限个独立集合的并集构成.文献［3］中，作者研究了一类在有限维空间中分离优化问题的一阶最优性条件并且通过对均衡问题指标集的划分，将均衡问题转化为约束集为有限维空间中有限个凸多面体的并集的分离优化问题，最终得到了此类问题的一阶最优性条件.在有限维空间中广义凸多面体与凸多面体是等价的，然而在无限维空间中，两者的定义是截然不同的.该文是在此基础上将有限维的情况推广到无穷维Banach空间，分析了约束集是有限个广义凸多面并集的分离优化问题的一阶最优性条件.

1 预备知识

约束集为抽象集合的优化问题如下:

定义问题(1)的可行域为Φ={x∈X:g(x)∈K}.

定义1设是问题(1)的可行点，

(Ⅰ)若条件0∈Δf()+(Δg())*(g()，K)在点成立，则点是问题(1)的强稳定点.

(Ⅱ)若条件0∈Δf()+(Δg())*×N(g()，K)在点成立，则点是问题(1)的M稳定点.当K是凸集时，N(g()，K)(g()，K)，即在K是凸的情况下，M稳定点和强稳定点是等价的.

定义2设是问题(1)的可行点，

(Ⅰ)若条件TΦ()={u∈X:Δg()u∈TK(g())}=:LΦ()在点成立，则称广义阿贝德型约束品性(GACQ)在点成立.

(Ⅱ)若条件N;Φ())⊂(LΦ())-在点成立，则称广义纳特型约束品性(GGCQ)在点成立.

明显地，因为(;Φ)⊂(TΦ())-，所以若(GACQ)在点成立，则(GGCQ)也在点成立.

引理1［2］(广义Fakas引理)设X和Y是Banach空间，是A:X→Y线性连续映射且像是闭的，ai∈X*，i=1，2，…，p，则

的负极锥可以写成如下形式:

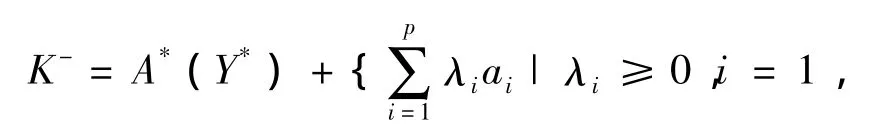
…，p}

引理2［1］设是 Banach 空间中有限个非空闭集的并，∈K且定义积极指标集为Ⅰ()={i∈∈Ki}，则有

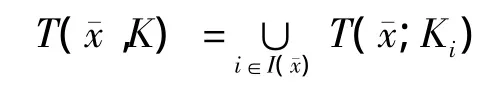
进一步，若Ki，i∈Ⅰ是凸的，则

此引理的证明详见文献［1］中性质3.1.该文中基本记号文献［4］.

2 主要结论

该文主要研究下述分离优化问题的最优性条件:

其中Ki，i∈Ⅰ={1，…，m}是Y中的广义凸多面体，X和Y是Banach空间，f:X→R和g:X→Y连续可微映射，约束集K是有限多个广义凸多面体集Ki的并.

设∈Φ，定义极值映射L:Y⇒X:

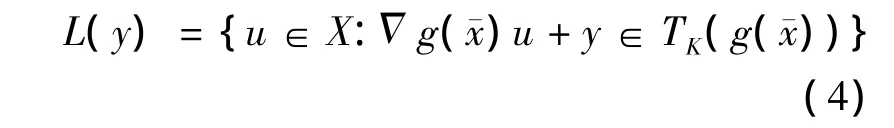
命题1 设K是Y中的非空闭集，g:X→Y是连续可微映射，∈g-1(K)且Φ为定义中的集值映射.若Φ在点(0，)是calm的，则

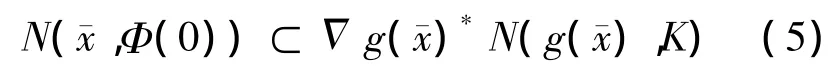
证明 定义函数f(y，x)=y+g(x)，其中(y，x)∈Y×X.因为g是连续可微的，故f:Y×X→Y在(0，)点是连续可微的且是满射.由文献［4］中的定理1.17，

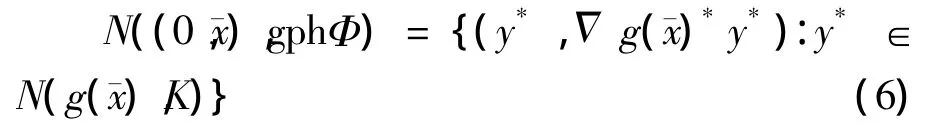
下面证明对任意的x*∈N(，Φ(0))，存在y*∈Y*使得(y*，x*)∈N((0，)，gphΦ).

因为x*∈N(，Φ(0))，故对任意的k∈N，存在使得x*.因为是有界的，故存在一个有界序列λk使得，由文献［4］中引理1.35和引理1.84知，对任意的γ＞0，函数

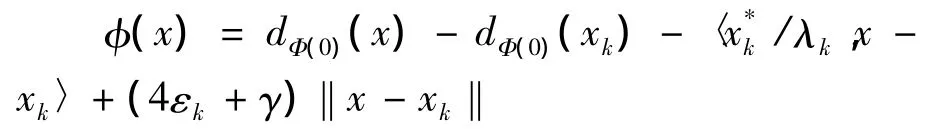
在xk点达到局部最小值，即存在rk↓0，使得对∀x∈B(xk，rk)有

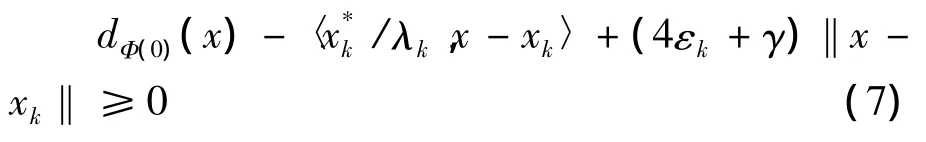
由题设知Φ在点(0，)是calm的，故存在r＞0和L＞0，使得对∀y∈B(0，r)，有

由公式(7)和(8)知，当k充分大时，函数

在点(0，xk)∈gphΦ点达到局部最小值.由文献［5］中引理4.3.4知，对于充分大的，函数φ(y，x)+dgphΦ(y，x)在(0，xk)点达到一个无约束的局部极小值.进而由［4］中引理5.3可知，存在∈LB(Y*)使得0+(4εk+γ)B(X*)+N((0，xk)，gphΦ).令k→∞ 和γ→0，则有*∈LB(Y*)和λ＞0，使得(*，x*/λ)∈N((0，)，gphΦ)，其中且λk→λ.因为N((0，)，gphΦ)是一个锥，故有(*，x*/λ)∈N((0，)，gphΦ)成立.由(6)能够推出(5)，命题得证.

定理1设是问题(3)的局部极小值点，若在点满足广义型约束品性(GGCQ)，则是问题(3)的M稳定点.

证明因为在点满足(GGCQ)，由文献［4］中命题5.1可知0∈Δf()+L(0)-.进一步，由负极锥的定义可知，u=0是下述优化问题的解:

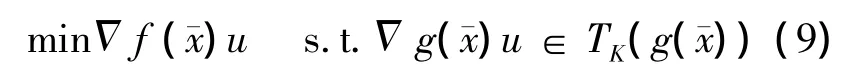
由公式(4)中L的定义可知，问题(9)的约束集可以等价为u∈L(0).因为Ki是广义凸多面体，则T(g()，Ki)是广义凸多面体锥.故由引理2知，

是有限个广义凸多面体锥的并集，由文献［2］中定理2.207和定理2.208知，L在0点是上lipschitz的，故L在(0，0)点是calm.由命题1，有

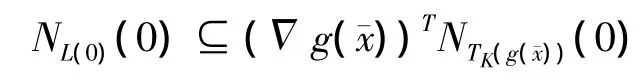
又因为广义凸多面体是满足conical性质的，故NTK(g(x))(0)=NK(g())成立.最后，因为u=0是优化问题(9)的解，故由文献［4］中命题5.1，优化问题(9)的最优性条件可以表示为

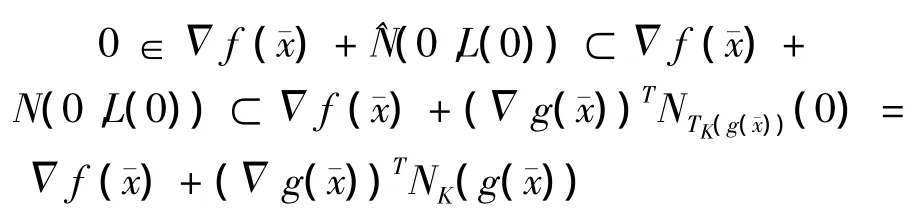
故满足M稳定点定义，定理得证.

定义2设是问题(3)的局部极小值点，若条件

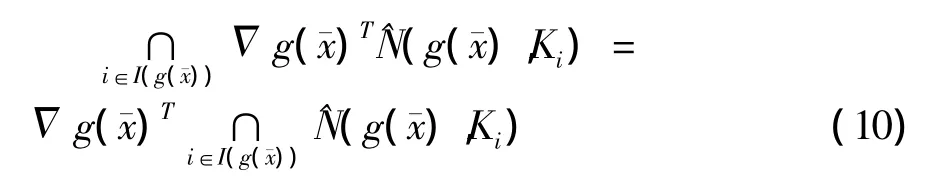
成立，称交叉性质在点满足.

定理2设是问题(3)的局部极小值点，若在点满足纳特型约束品性(GGCQ)和交叉性质(10)，则是问题(3)的强稳定点.

证明 由定理1的证明过程，本定理从下式开始证明

由公式(4)和引理1知，

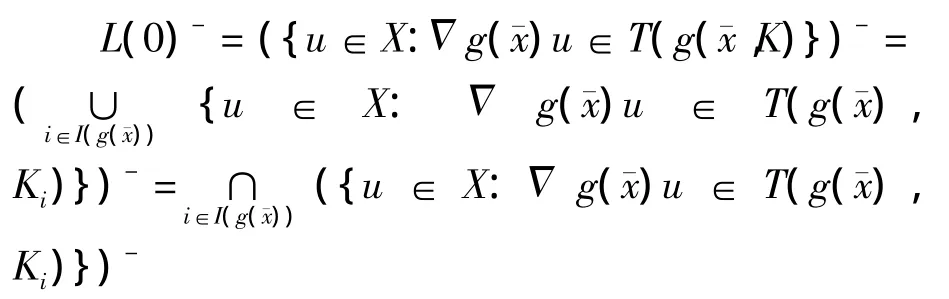
因为Ki是广义凸多面体，则T(g()，Ki)是广义凸多面体锥.不妨假设存在，A是从Y到Z的一个连续线性映射，使得

又因为A是线性连续映射，故对∀i∈Ⅰ，有

由引理1可知，

上式由交叉性质和引理2可得.故L(0)-=，则

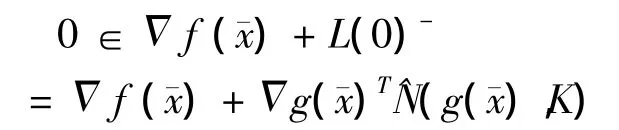
故由强稳点定定义可知，命题得证.

［1］ Ban Liqun，Boris S，Mordukhovich，Song Wen.Lipschitzian Stability of the Parameterized Variational Inequalities over Generalized Polyhedron in Reflexive Banach Spaces.Nonlinear Anal，2011，74:441-461.

［2］ Bonnans J F，Shapiro A.Perturbation Analysis of Optimization Problems.Springer，New York，2000.

［3］ Flegel M L，Kanzow C，Outrata J V.Optimality Conditions for Disjunctive Programs with Application to Mathematical Programs with Equilibrium Constraints.Set-Valued Anal，2007，15:139-162.

［4］ Mordukhovich B S.Variational Analysis and Generalized Differentiation I:Basic Theory.Springer，Berlin，2006.

［5］ Clarke F H.Optimization and Nonsmooth Analysis.Wiley，New York，1983.