一类远期启动林木期货期权定价*

陶原峰，王玉文

(哈尔滨师范大学)

0 引言

当前我国林业资源有限，但需求量很大.国家林业局出台了关于加强林木采伐许可证核发管理工作的通知，严格执行采伐制度.因此如何在市场中利用金融衍生品来保障各类参与者的利益，降低参与者的风险成为了一个引人关注的问题.大商所已对林木期货合约进行立项，随后还会有其他相关的衍生品陆续推出.

期货期权的持有者有权利在将来一定时刻以约定的期货价格进入期货合约.1982年，美国长期国债期货期权在芝加哥期货交易所上市，引发了期货交易的一场革命.期货期权交易不仅对于现货商，对于期货商也起到了一定的规避风险的作用.相对于关于标的资产的期权，期货期权合约以其流动性更好，更容易交易，交易费用更低的优点吸引了很多投资者.在期权的研究中，定价是核心问题.期货价格的行为的变化直接导致了期权定价模型的有效性.1973年，Black和Scholes得出了著名的Black-Scholes期权定价模型［1］.在该模型基础上，Black在 1976年给出了期货期权的定价模型.Cox，Ingersoll和 Ross(1981)在非随机风险中性利率假设下，进一步扩展了Black期货期权定价模型［2］.

该文介绍一种远期启动的林木期货期权，木材需求者在当前时刻可以提前支付一定金额，然后无须支付额外金额即可在未来的某时刻，也就是商品林林木所有人取得林权证时拥有一份期货期权，在期权的到期日，此时商品林林木所有人已获得采伐权可以选择执行期权来以约定的金额进入一份期货合约，若之前的敲定价格不利也可以选择放弃期权.

该文主要应用随机分析中的Girsanov定理.

引理1［1］(Girsanov定理)假定{Wt}是一个P-布朗运动，其自然σ-域流是，且是 一 个适应过程，使得

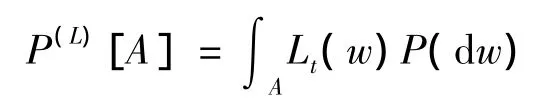
是一个标准的布朗运动.

1 数学模型

假定市场是无套利，有效，无摩擦，从而存在风险中性的鞅测度，利用上述引理构造等价鞅测度Q，找到Q关于P的Radon-Nikodym导数中的θ，使得在测度Q下资产的贴现价格是鞅，从而利用鞅方法进行定价.

合约模型:持有人在未来的T0时刻(林木所有人已具有林权证)在无须支付额外费用的情况下拥有一份敲定价为FT0，到期日为T1(此时林木所有人已具有采伐证)的期货期权，T1＞T0，相应的期货合约到期日为T2＞T1.期货合约开始于T0时刻.无风险利率为r.求在t＜T0时刻的期权价格.

定理1 对于T0之前的t时刻，远期启动的期货期权价格由下式给出

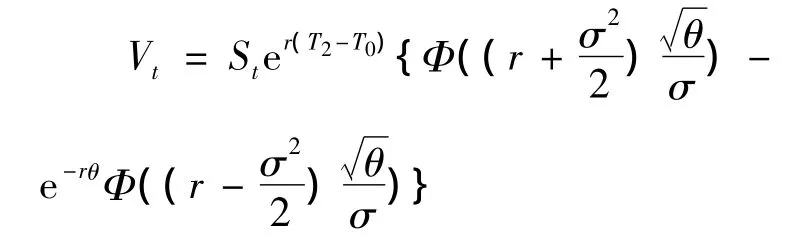
其中θ=T1-T0

证明 设林木的市场价格St服从几何布朗运动St=S0exp(νt+σWt)，则对应的到期日为T2的期货合约价格为［4］

设

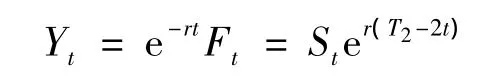
应用伊藤公式有

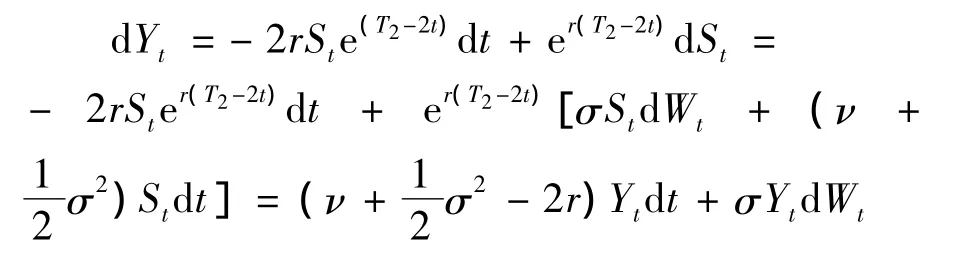
由引理可知，{Yt}t≥0为Q-鞅，则由

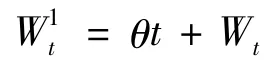
特别在t=T1时刻，有

在期权到期日T1，如果期货期权被执行，期权持有人收益等于期货价格和敲定价格的差.由资产定价基本定理，对于t∈［T0，T1］，记 τ=T1-t，有

其中Q为上面构造的概率测度，在该测度下期货合约贴现价格是个鞅.因为在测度Q和条件下为Q-标准布朗运动，从而是一个期望为0，方差为τ的正态分布随机变量，进行标准化，令，则服从标准正态分布.从而有

首先由被积函数非零确定Z的范围，整理得

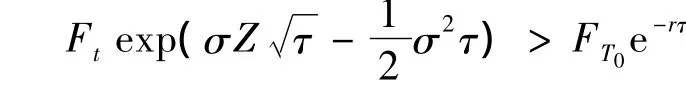
等价于

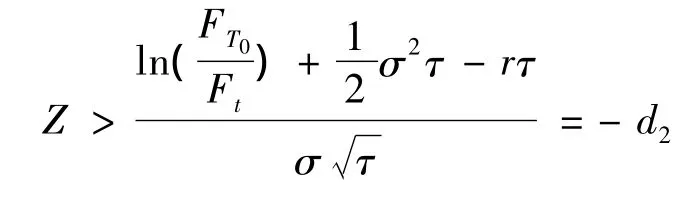
代入有

其中

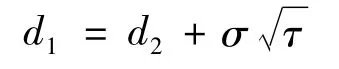
特别地，在T0时刻，有

记θ=T1-T0，则有

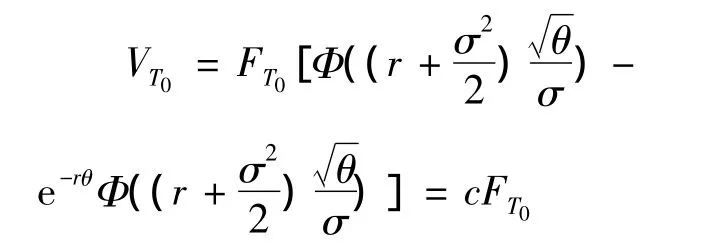
其中c=c(r，σ，T1，T0)与期货价格无关.

对于t＜T0，此时不适合用期货价格定价.注意到在T0时刻的期权可以有c份林木期货合约复制，又由于

从而有

其中a=a(r，σ，T0，T1，T2)与林木价格无关.对于t＜T0，期权价格可由aSt给出，即

得证.

［1］ Black F，Scholes M.The Pricing of Options and Corporate Liabilities［J］.The Journal of Political Economy，1976，81(3):637-654.

［2］ Cox J C，Ingersoll J E，Ross S A.The Relation between Forward Prices and Futures Prices［J］.Journal of Financial Economics，1981，9(4):321-346.

［3］ 埃瑟里奇.金融数学教程［M］.张寄洲，译.北京:人民邮电出版社，2006.

［4］ Hull J C.期权、期货及其他衍生品(第七版)［M］.王勇，索吾林，译.北京:机械工业出版社，2009.