相贯线的图示方法比较分析及其简化

林春江 丁 雨

(大连海洋大学，辽宁大连116300)

相贯线的图示方法比较分析及其简化

林春江 丁 雨

(大连海洋大学，辽宁大连116300)

相贯线一直是让人挠头的教学难点问题。针对不同的专业领域，文章从相贯线的绘制精确度、方法的简捷实用性、学生的可接受性和对制图学习的迁移影响等方面加以分析和比较，总结提出了与之相适应的解决办法，即在教学设计上，贯彻相贯线的简化作图，或将成为破解相贯线教学难点的关键。

相贯线;比较分析;表面求点法;近似画法;三点法;简化

工程制图上，表达工程构件中由两立体表面相交而产生的轮廓线称之为相贯线。其形状可因两立体及其相对位置不同而各异，且大多为空间曲线。相贯线作为工程构件中常见的轮廓形状，对其在工程图样中的图示表达是不可避免的问题。但是，相贯线的绘制求解方法涉及较难理解的图学理论与方法，学生对此常感到挠头，历来是教学难点。如何针对不同的专业领域，从相贯线的绘制精确度、方法的简捷实用性、学生的可接受性和对制图学习的迁移影响等方面加以分析和比较，总结提出与之相应的解决办法，对教学具有现实指导意义。

工程实际中，最为常见的是两圆柱正交的相贯线，其绘制方法也有多种。另外，用 CAD(计算机辅助设计)制图的技术已普遍应用。因此，基于这种情况选取了几种常见的两圆柱正交作为案例分析。

1. 几种圆柱相贯线绘制方法案例

1.1 表面求点法

相贯线是两个立体表面的共有线，相贯线上的点同时属于两立体表面，因此，求作相贯线常利用立体表面求点的方法来解决，这是表面求点法求相贯线的理论基础。在此基础上，又分为利用立体表面投影积聚性求点法、辅助平面法求点及辅助球面法求点等完成相贯线的求解作图［1］。图1是利用立体表面投影积聚性求点法作两圆柱正交的相贯线图例。其主要步骤如下所述:

图1 表面求点法求相贯线

① 求特殊点Ⅰ、Ⅲ、Ⅴ、Ⅷ，用对象捕捉追踪功能确定。见图1(a)。

② 求一般点Ⅱ、Ⅳ、Ⅵ、Ⅷ，用偏移(Offset)命令，以y偏距确定2、4、6、8及2″4″6″8″，进而求出2'、4'、6'、8'。见图1(b)。

③ 发出Spline(样条曲线)命令绘制出空间相贯曲线，如图1(c)所示。若求作更多一些一般点，曲线的形状会更精确。

1.2 三点法

分析求出理论相贯线上三个特殊点Ⅰ、Ⅲ、Ⅴ已知的投影1'、3'、5';1、3、5;1″3″5″，见图2(a)。以此三点为基础，可用两种绘制命令，但绘制结果有所不同。

方法一，以Spline(样条曲线)命令绘制出空间相贯曲线如图2(b)所示。

方法二，以圆弧(Arc)命令中“三点”画圆弧方式画出1'、3'、5'三点确定的圆弧，代替理论相贯线，如图 2 (c)所示。

图2 三点法求相贯线

1.3 近似画法

用近似画法绘制相贯线的条件是:当两正交圆柱直径相差较大且作图精确度要求不高时，可以圆弧代替理论相贯线，与三点法不同的是，该圆弧是取参与相贯的大圆柱底圆半径R为其半径，用绘制圆弧(Arc)命令，以起点1'、端点5'、半径 R为条件方式完成作图，如图3(b)所示。

图3 近似画法求相贯线

图4 几种相贯线画法的比较

2. 几种图示方法的比较分析

2.1 精确度分析

精确度分析是指用某种图示方法绘制的相贯线与理论相贯线的精准程度。通过图4对三种图示结果来看，其精准度从高到低，依次为表面求点法、三点法和近似画法。另外，当用三点法一(样条曲线)时，其精确度与表面求点法相近，见图4(a);若用三点法二(圆弧)时，其精确度与近似画法相当，见图4(b)。这为其选用提供了灵活性。

2.2 简捷实用性分析

简捷实用性分析，着重是看作图过程明晰，方法简捷实用，既不失去表达的原意，又不会引起误解或产生理解的多义性［2］。其实质是强调了简化作图，这符合GB/T16675.1－1996《技术制图简化表示法》的规定。通过图2、3看出表面求点法较为繁琐，三点法和近似画法作图相对方便简捷。

2.3 可接受性分析

可接受性是教学过程中必须遵循的一个重要原则。同样的问题对不同的学生，其可接受性将会不同。但是通过统一考试录取的同班学生来说，又有其可比性。在同等条件因素下，学生容易接受的方法，自然有其可取之处。在三种方法中，三点法既有理性的作图原理分析，又提供了简便的作图方法，自然更容易接受。表面求点法作图原理方法相对复杂，不易理解接受。

2.4 迁移影响分析

迁移是指一种学习对另一种学习的影响［3］，且具有二重性，既可产生正向迁移促进学习，也可能产生负向迁移阻碍学习的深化。用表面求点法绘制相贯线，整个作图过程中，思维活跃，逻辑性强，便于学生理解记忆，做到举一反三，有利于正向迁移的发生。而用近似画法，则需机械性记忆，使得思维消极，不利于学生培养科学的思维品质。

3. 相贯线图示方法的应用与选择

上述分析结果证明:相贯线的各绘制方法各有其长短，选用时应根据不同专业技术领域对教学目标的要求，有所侧重地来选择不同的绘制方法，做到有的放矢。

对相贯线精确度的要求，依据其工程图样应用的专业技术领域的不同而不同。对于石油化工管道、农业机械、船舶等行业的工程图样，其中应用焊接成型工艺较多，常需要作展开放样图等。其相贯线的绘制应重点考虑精准程度因素，以选择表面求点法等精确作图方法为宜。

对于以热加工为主要技术支撑的机械制造行业，机件多为铸造工艺成型。在这类工程图样中绘制相贯线，过分要求其精准度则是没有必要的，则应以方法便捷实用作为首选，宜采用近似简化画法或三点法。

从教学的角度考虑，三点法折中，兼有表面求点法与近似画法的长处，其中，方法一绘制的相贯线，其作图较表面求点法简便，精确度与之靠近;方法二绘制的相贯线其作图方法及结果与近似画法相近。这两种方法对于学生理解作图原理过程及绘制操作容易掌握等方面均有长处，同时在较大程度上促进了学习的正向迁移，值得推广。

4. 结论

当前，图样简化在国内外图学教育与应用领域得到普遍重视。现今，在各校工程制图教学学时大为减少的情况下，在教学设计上，贯彻相贯线的简化作图或成为趋势。这对合理利用教学课时和提高设计制图效率均有裨益，或成为破解相贯线教学难点的关键。而且，在 GB/T16675.1－1996《技术制图简化表示法》中可寻到图样简化的权威性依据。其中规定了相贯线简化作图原则，指出“在不引起误解时，图形中的过渡线、相贯线可以简化，例如用圆弧或直线代替非圆曲线”，“也可以采用模糊画法表示相贯线”，并表列简化作图范例［4］，如图5所示。这为在教学及图样绘制实践中的示范应用提供了指导与发挥空间。目前，简化作图在教学及应用上贯彻的力度还不够大。案例中仅对两圆柱正交时的相贯线简化方法作了重点分析。依据国家标准规定，可将分析比较结果引申应用到圆柱与圆锥、圆柱与圆柱斜交等状况下绘制简化的相贯线。如在图6中给出的示例，是采用三点法绘制的。但这种方法示例，目前在国内工程制图教材中可能尚不多见，其可行性将有待于进一步探讨和论证。

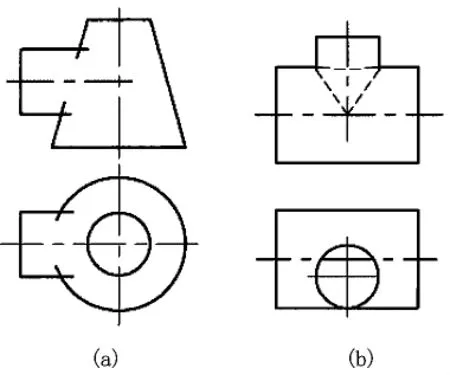
图5 制图标准中相贯线简化作图示例

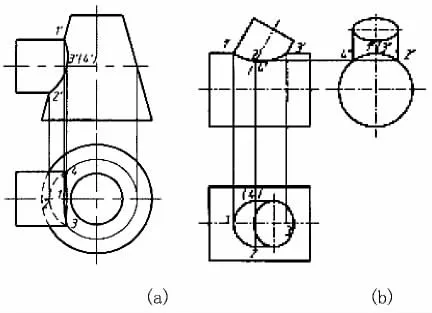
图6 圆柱与圆锥、圆柱斜交的相贯线

［1］ 金大鹰.机械制图［M］.北京:机械工业出版社，2009.83－87.

［2］ 国家技术监督局.技术制图简化表示法［M］.北京:中国标准出版社，1997.2.

［3］ 骆伯巍.教学心理学原理［M］.杭州:浙江大学出版社，2004.153.

［4］ 国家技术监督局.技术制图简化表示法［M］.北京:中国标准出版社，1997.11.

(责任编辑 陈永康)

book=34,ebook=34

TH126

A

1008－7257(2012)02－0073－02

2012－04－07

林春江(1954－)，男，辽宁大连人，大连海洋大学教授，主要研究方向为工程图学教育及CAD等。