基于Kalman滤波技术的纤维增强复合材料界面断裂参数确定方法

何周理 徐绯， 段敏鸽

(1.西北工业大学航空学院，西安 710072;2.上海飞机设计研究院，上海 200232)

连续碳(及碳化硅)纤维增强复合材料具有较高的比强度、比刚度以及耐高温、耐腐蚀、抗氧化、低密度等优点，因此，已越来越广泛地应用于航空、航天等高温领域。

在固体力学和材料力学领域中，某些材料参数通过试验直接测量十分困难。但却可以通过试验测量得到与这些材料参数直接相关的其它物理量，再考虑通过反演计算得到所需的材料参数值。常用的反演方法主要包括:Monte Carlo［1］法、模拟退火法［2］、遗传算法［3］、改进的人工神经网络法［4］等等。上述的几种反演方法属于完全非线性反演法，具备全局搜索能力，但是计算量往往很大，计算效率不高。所以对于单个或者未知参数较少时的反演情况，上述方法并非最佳选择。本文将介绍一种计算效率较高的Kalman滤波反演法。

1960年，Kalman提出了用递归方法解决离散数据线性滤波问题。此后，由于数字计算技术的进步，Kalman滤波技术得到了广泛的应用，特别是在自主及协助导航领域。Kalman滤波可由一系列递归数学公式描述，它们提供了一种高效的方法来估计过程的状态，并使估计均方误差最小［5］。其应用广泛且功能强大，即使对相应模型的性质不确定，可以估计信号的过去和当前状态，甚至将来的状态。基于以上Kalman滤波反演方法的优点，促使其正逐渐走进研究者的视野，如结合边界元利用扩展的Kalman滤波方法对材料弹性和热弹性参数［6］进行反分析;利用Kalman滤波方法对金属材料的Gurson模型参数［7，8］进行反演确定;利用扩展的 Kalman滤波对单一载荷下裂纹断裂参数和动态界面分层参数进行反演确定［9，10］;大体积混凝土结构位移场参数［11］的反演等等

本工作介绍了Kalman滤波反演方法的基本原理，并且结合SiC(SCS-6)/Ti复合材料的单纤维顶出试验，成功地反演出了碳化硅纤维钛基复合材料的界面参数。论证了Kalman滤波反演法具有较好的收敛性和较高的精确性。并且通过不同的测量噪音证明了其具有一定的消除噪音的能力。通过例证还可看出，Kalman滤波反演方法可在一定程度上简化实验方案［12］。

1 纤维顶出试验研究

单纤维顶出试验［13］是从细观上对纤维增强基体复合材料界面性能进行研究的一种试验手段，主要用于获得纤维和基体交界处的界面性能，比如界面的剪切强度、拉伸强度以及断裂能等等。单纤维顶出试验的实验示意图和试验结果曲线如图1、图2所示，实验机通过压头施加压力把纤维从基体中顶出，同时测量出压头的支反力和位移。

从试验曲线可以看出初始载荷随位移呈线性增加，当载荷增加到Fmax时，表示界面剪切应力达到最大值，界面开始脱粘，此后载荷开始直线下降。由试验曲线可以获得2个重要的参数Fmax以及与Fmax对应的位移δmax。然后根据公式:

上式中d是纤维的直径，L是试样的长度，通过上式计算得到界面的试验剪切强度。由于在上述试验中获得的界面剪切强度τ为纤维脱粘时整个界面的剪切应力平均值，然而在实际情况中，纤维脱粘时沿纤维轴向的拉伸应力和剪切应力分布都是不均匀的，所以上述试验中获得的界面剪切强度并非材料界面的真正剪切强度［14］。为了得到纤维增强复合材料界面的真实剪切强度，很多研究者运用有限元模拟计算来反演界面剪切强度。如文献［9］中关于正问题的研究，成功地用cohesive单元模拟单纤维顶出试验，得到了纤维脱粘时切应力沿界面的分布，通过有限元计算得到的力-位移曲线和试验的结果基本一致。在本文的研究中我们用反问题思路，即考虑界面剪切强度和断裂能量都为未知参数，通过参考文献［15］中试验得到的力-位移曲线结果，结合Kalman滤波反演技术来反演计算未知的两个参数。

有限元模型，试验模型可看成轴对称模型所以在模拟计算中用轴对称条件进行简化。简化后的有限元模型及尺寸如图3所示，图中显示了对称轴和界面的位置，分别标识了压头端和简支座端，对称轴采用对称边界条件，简支端限制Z向位移，加载端Z向位移0.09mm。

图3 简化的有限元模型Fig.3 the FEA model

2 Kalman滤波原理简介

简单来说，Kalman滤波是一个优化自回归数据处理算法，用递归的方法解决离散数据线性滤波问题。Kalman滤波应用广泛且功能强大，他的广泛应用已经超过30年，包括机器人导航、控制、传感器数据融合甚至在军事方面的雷达系统以及导弹追踪等等。近年来更被应用于计算机图像处理，例如头脸识别、图像分割及图像边缘检测等等。Kalman滤波器的基本工作原理主要由时间更新(预测)和量测更新(校正)两部分组成，原理公式如表1中所示。

式(2)表示由k－1时刻的状态变量xk－1递推k时刻的状态变量xk;式(3)表示估计误差协方差的递推公式;式(4)表示量测向量zk在状态变量xk时的函数表达。其中P－k为先验估计误差协方差矩阵，R为量测噪音协方差矩阵;A表示差分方程的增益矩阵，B代表可选的控制输入u∈Rl的增益矩阵，wk－1表示过程激励误差;h表示状态变量xk对量测变量zk的增益函数，向量vk表示量测误差。估计误差协方差Pk和量测误差协方差R都随着时间步k的变化而不同。Hk为k时刻量测变量值对状态变量(待估参数)的一阶偏导数:

当Kalman滤波的过程激励噪音wk=0、增益矩阵A为单位矩阵I、控制输入u=0时，Kalman

滤波的状态更新方程简化为为:

Kalman滤波器向估计误差协方差矩阵更新方程为:

表1 Kalman滤波原理(-代表先验，^代表估计)Kalman filter principle table(-is priori state estimate，^denote estimate)

3 Kalman滤波反演步骤

(1)首先假设待估参数的初值:取状态变量的初值为x0和误差协方差初值为P0。

(2)把第k步的状态变量值和已知的各材料参数代入到有限元模型计算中，得到计算量测向量;并且提取有限元结果计算出Hk。

(4)根据第k步的值计算Kalman增益矩阵Kk+1。

(6)检验更新的误差协方差矩阵的最大特征值是否达到预设的精度ε。

(7)如果没有达到精度要求则重复反演计算步骤2－6;如果达到精度要求则停止滤波反演计算。

4 实例证明

4.1 例证1

在第1节中已经说明了单纤维顶出试验得到的是复合材料界面的平均性能，而非界面的真实性能。本例将使用Kalman滤波反演法来求解真实的剪切强度τb，设界面的剪切强度τb为未知参量，即状态向量为xk=τbk;以压头支反力的最大值为Kalman滤波的量测标准，即量测向量为zk=Fmax。本例中状态向量只有一个参数，所以属于一维的Kalman滤波反演计算。在反演计算中，力的单位为N，剪切强度的单位为MPa，位移的单位为mm。

表2 Kalman滤波器的参数设置Table 2 The initial parameters of Kalman filter

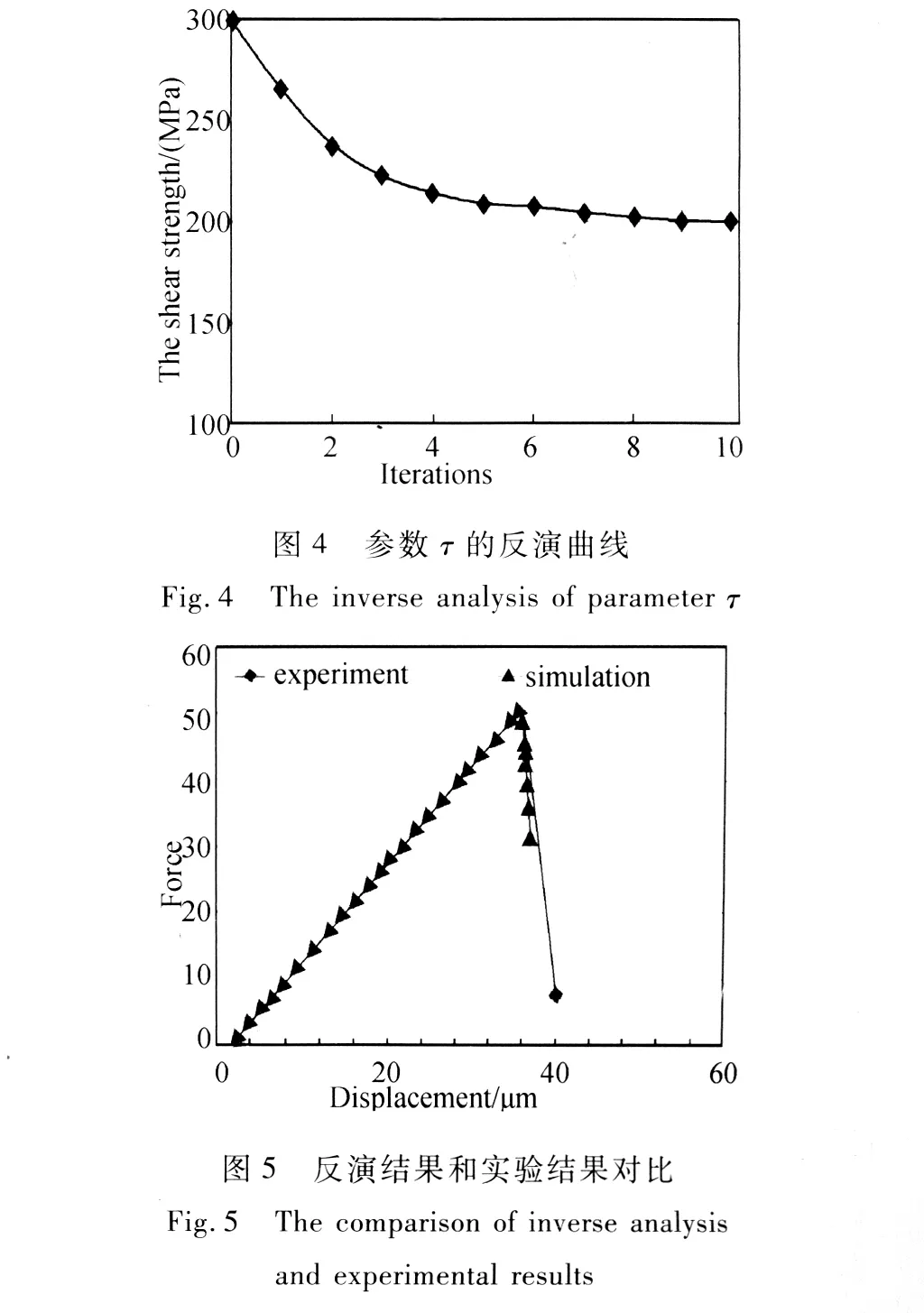
Kalman滤波反演计算的每一步更新中必须已知试验量测向量Zk+1和Hk的值，所以针对不同的状态变量xk，结合有限元计算可得到所需的计算量测向量z－k和Hk，然后可以使Kalman滤波反演计算向后一步一步进行预估校正。当即估计误差的协方差小于等于1时，认为找到合适的反演结果。把上述初始估计和误差协方差矩阵代入Kalman滤波反演计算中。当经过10次反演计算后最终误差矩阵协方差为0.999，反演结果为 200.8MPa，反演数值曲线如图4所示。

把得到的参数xk=τbf=200.8 MPa代入到数值模拟计算中，计算得到的力-位移曲线如图5所示，与试验得到的力-位移曲线相比较，两者基本吻合，证明了此方法的可行性和精确性。

4.2 例证2

运用Kalman滤波反演法确定单纤维增强复合材料界面的多个未知参数。界面的剪切强度τb和断裂能均为未知参量，即状态向量为xk=［τ，G］T，所以本例的计算属于二维的Kalman滤波反演计算。在反演计算中以压头的压力和对应的下压位移为反演的量测标准，即量测向量为zk=［Fmax，δ］。在计算中，力的单位为N，剪切强度的单位为MPa，位移的单位为mm，断裂能的单位为N/mm。本例进行计算的初始参数设置如下。

初始状态变量:

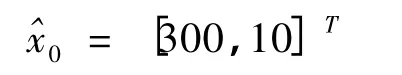
初始估计误差的协方差矩阵:

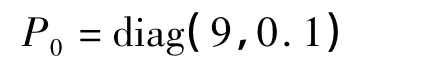
观测误差的协方差矩阵:

过程激励噪声方差矩阵:

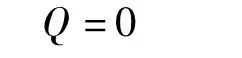
把上面的的各个值结合有限元计算可得到反演所需的Zk和Hk，然后按照Kalman滤波反演计算的步骤一步一步向后进行反演计算。当(即估计误差的协方差矩阵的最大特征值小于等于1时)，认为反演值达到要求的精度，找到了合适的反演结果。本例中的观测误差协方差矩阵为:R=diag(2.5，2.5)，当经过44次反演计算后得到结果为xk=［τ，G］T为［200.555，3.9548］T，最终的误差协方差为过程激励噪声方差矩阵:P44=diag(0.9983，0.001)，得到参数 τ和 G的反演曲线如图5所示。

把反演得到的参数τ和G代入到有限元计算中的界面模型中，进行数值模拟计算，最后计算得到的力－位移曲线如6图所示，并且和试验得到的力－位移曲线相比较。由图6中可以看出，最后的反演结果计算得到的曲线和试验得到的曲线基本重合，所以反演的结果为精确值。另外随着反演的参数增多，滤波次数明显增多。

4.3 例子3

研究量测噪音误差对反演结果的影响，例2中其它各参数不变，而仅仅把量测噪音误差协方差分别设为 diag(1，1)，diag(5，5)和 diag(16，16)，相对应的试验误差分别为2%，4.5%和8%的情况。按照例2的步骤进行Kalman滤波反演计算，得到的结果如表3示。

图6 剪切强度(τ)(a)和断裂能(G)(b)的反演曲线Fig.6 The inverse analysis of shear strength(τ)(a)and the fracture energy(G)(b)

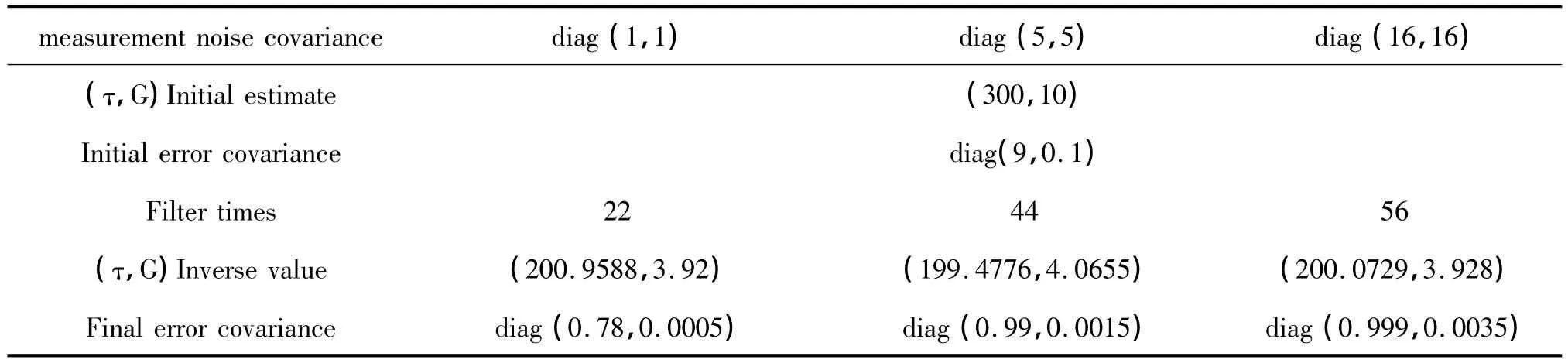
表3 不同的量测噪音协方差Kalman滤波反演结果Table 3 The results of influence of noise by Kalman filter

图7 反演结果和实验结果对比Fig.7 Comparison of inverse analysis and experimental results

表3说明Kalman滤波反演计算具有一定的消除噪音的能力，由不同的测量噪音误差协方差得到的反演结果具有一致性;但是随着噪音的增大，滤波的次数要明显增多。

5 结论

通过对SiC(SCS－6)/Ti单纤维增强复合材料的界面参数计算研究表明:

(1)Kalman滤波反演方法不论对于单个参数反演还是多个参数反演都是可行的，由图4和图6可知Kalman滤波反演法的收敛性较好。

(2)图3和图7的例证结果表明反演得到的结果和试验得到的结果［9］吻合很好，说明Kalman滤波反演方法具有较高的精度。

(3)Kalman滤波反演方法可以引入不同的量测噪音协方差矩阵，说明实验噪声的影响，这也是该方法作为材料参数反演计算的一个重要特点和优点。

［1］姚姚.蒙特卡洛非线性反演方法及其应用［M］.北京:冶金工业出版社，1997.

［2］KIRKPAT rick S，CELATT C D，VECCHI M P.Optimization by simulated annealing［J］.Sciences，1983，220:671－680.

［3］师学明，王家映.地球物理资料非线性反演方法讲座(四)遗传算法［J］.工程地球物理学报，2008，5(2):129－140.

［4］靳蕃，范俊波，谭永东.神经网络与神经计算机原理应用［M］.成都:西南交通大学出版社，1997.

［5］KALMAN RE.A new approach to linear filtering and prediction problems［J］.Transaction of the ASME—Journal of Basic Engineering，1960，82:35 －45.

［6］王元淳，孙浩.弹性、热弹性物性值反问题的边界元分析［J］.计算结构力学及其应用，1993，10(4):490－494.

［7］AOKI Shigeru，AMAYA Kenji，SUGA Kazuhiro，et al.Identification of Gurson’s Material Constants by Using Kalman-Filter［J］.Transactions of the JapanSociety of Mechanical Engineers，2001，67(664):1892 －1897.

［8］ALBERTO C，STEFANO M，BARBARA O.Identification of Gurson-Tvergaard material constants by using Kalman filtering technique I Theory［J］.International Journal of Fracture，2000，104(4):349 －373.

［9］BOLZON G，FEDEL R，MAIER G.Parameter identification of a cohesive crack model by Kalmanfilter［J］.Computer Methods in Applied Mechanics and Engineering，2002，191:2847 －2871.

［10］ALBERTO C，STEFANO M.Identification of a consititutive model for the simulation of time-dependent interlaminar debonding processes in composites［J］.Computer Methods in Applied Mechanics and Engineering，2002，191:1861 －1894.

［11］蔡汝铭，张剑，赵新铭.大体积混凝土位移场参数的卡尔曼滤波反演［J］.华北水利水电学院学报，2006，27(1):24－27.

［12］WELCH Greg，BISHOP Gary.An Introduction to the Kalman Filter［J］.UNC-Chapel Hill，2006，TR:95 － 041.

［13］KERANS R J，PARTHASARATHY TA.Theoretical A-nalysis of the Fiber Pull-Out and Push-Out Tests［J］.Journal of the American Ceramic Society，1991，74:1585 －1596.

［14］原梅妮，杨延清，马志军，等.SiC纤维增强钛基复合材料界面强度研究进展［J］.稀有金属材料与工程，2007，36:1115－1118.

［15］CHANDRA N，Li H，SHET C，et al.Some issues in the application of cohesive zone models for metal-ceramic interfaces［J］.International Journal of Solids and Structures，2002，39:2827 －2855.