不锈钢材料高温、高应变率下动态力学性能的试验研究

张 红， 索 涛， 李玉龙

(西北工业大学航空学院，西安 710072)

不锈钢是现代工业中的一种重要结构材料，广泛应用于航空、化工、能源等方面，对其力学性能的研究具有重要的价值。从现有对各类不锈钢材料的研究可发现:应变速率增加时，其真实应力、加工硬化率和应变率敏感性存在较大差异［1～3］;同时温度对这类材料的力学性能也有较大影响［1～6］。

而不锈钢结构件的加工、使用过程经常会涉及高温环境和动态载荷，因此有必要研究不锈钢材料在高温、高应变率耦合条件下的力学行为，以便为动态载荷下材料和结构的设计、加工及优化提供参考。例如，结构件的高速切削加工即为典型的高应变率、高温变形过程，对切削过程的仿真分析则必须提供相关的动态力学性能参数才能进行。但目前国内对不锈钢材料的研究多为高温准静态试验［4～6］和室温动态试验［7］的分别研究，高温、高应变率耦合力学性能的研究结果较少。为此，本文利用加装同步组装系统的高温Hopkinson压杆系统对某不锈钢材料高温、高应变率耦合状态下的动态力学性能进行了测试，得到了材料不同应变率和温度下的真实应力-应变曲线，并与准静态压缩结果对比，研究了材料的塑性流变行为，对其温度及应变率效应进行了分析。

1 试验条件及试验装置

1.1 试验条件

本工作对不锈钢的压缩试验涉及不同温度下的准静态和动态两种情况。准静态试验采用φ5mm×5mm圆柱试样在电子万能实验机上进行，通过控制加载速率使应变率保持在0.001s－1。试验温度为室温20℃ ，200℃ ，400℃ 。

动态试验选取1100s－1，2400s－1，4000s－1，8000s－1和 16000 s－1五种应变率。其中，1100 s－1和2400 s－1两种应变率下的压缩试验采用 φ5mm ×5mm的圆柱形试样，在直径12.7mm的分离式Hopkinson压杆上进行;应变率4000和8000 s－1试验采用 φ2mm ×2mm ，16000 s－1采用 φ2mm ×1mm 圆柱形试样在直径5mm的微型Hopkinson压杆［8］进行。试验温度为室温 20℃ ，200℃ ，400℃ ，600℃ ，800℃。为避免试样加热引起加载杆温度变化造成波阻抗变化影响试验准确性，高温时采用加装同步组装系统的高温 Hopkinson杆系统［9，10］实现高温、高应变率同时加载。

1.2 高温Hopkinson压杆系统

传统Hopkinson压杆由空气炮、子弹(撞击杆)、入射杆、透射杆、测试系统、支持系统组成［9］。其基本工作原理［9］是将试件夹在入射杆和透射杆之间，利用空气炮以一定速度发射子弹撞击加载杆产生压缩应力波，并通过入射杆和透射杆上粘贴的应变片记录入射波εI、反射波εR和透射波εT信号。根据一维应力波理论［11］，得到被测试样的应变率˙εS、应变εS、应力σS随时间的变化历程:

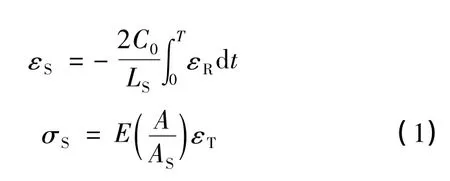
式中E，C0和A为加载杆弹性模量、纵波波速和横截面积，LS，AS为试样原始长度和横截面积。

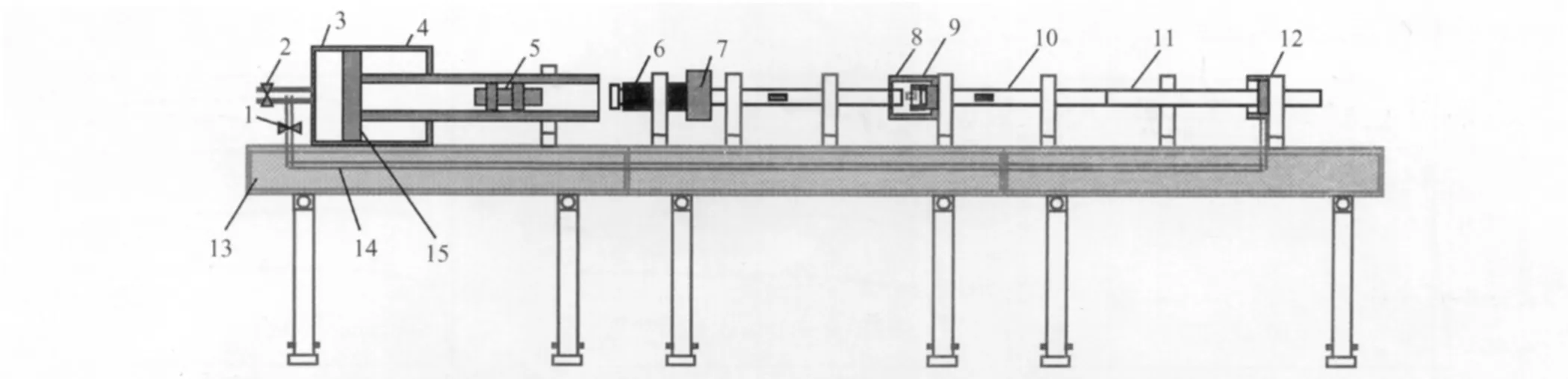
图1 带有同步组装系统的高温Hopkinson杆系统［9］Fig.1 High temperature Hopkinson bar with synchro assembly system 1—outlet valve;2—inlet valve;3—back air chamber;4—front air chamber;5—strike bar;6—incident bar;7—reaction mass;8—heating furnace;9—sample;10—transmitted bar;11—momentum trap bar;12—driver;13—support;14—air pipe;15—plunger.

由于在Hopkinson压杆试验过程中试样必须与两加载杆相接触，高温试验时若把试样和加载杆的杆端同时放于加热炉中进行加热，加载杆上将产生温度梯度，而温度的变化会引起波阻抗的变化。Hopkinson压杆实验中假设波阻抗沿加载杆长度方向不变，因此这种加热方法将对实验数据的处理造成诸多不便［13］。高温Hopkinson压杆系统则只对与加载杆分离的试样单独加热，并利用同步组装系统，实现加载应力波到达入射杆与试样接触面之前，预加热试样、入射杆和透射杆在毫秒量级时间内充分接触，克服了加载杆温度变化及弹性杆过热等一系列问题［9，10］。图 1 为高温 Hopkinson 压杆系统的工作原理图，装置的详细介绍参阅文献［9，10］。

2 试验结果分析与讨论

2.1 试验结果分析

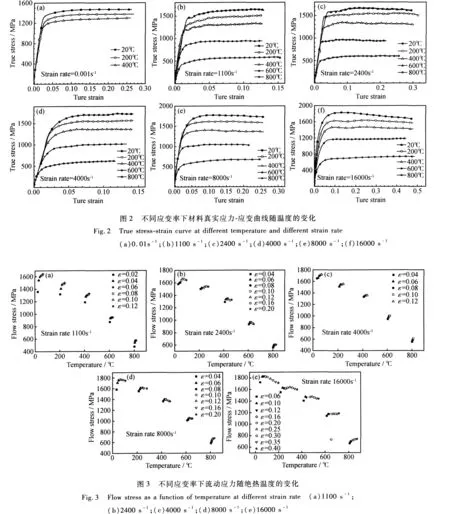
图2给出了不锈钢在准静态及 1100s－1，2400s－1，4000s－1，8000s－1和 16000s－1应变率下不同温度的真实应力-应变曲线。由图可知，该不锈钢材料具有明显的温度和应变率敏感性。准静态及动态加载时材料的流动应力均随温度升高显著降低，存在明显的热软化效应;同一温度下，动态加载时材料的流动应力均高于准静态，且流动应力随应变率增加而增大。

动态压缩过程中，较低应变率下材料的真实应力-应变曲线与准静态时变化规律相似，存在微弱的应变硬化现象，但高温高应变率下变形规律与准静态结果存在明显差异。当应变率达到2400s－1时，材料在各试验温度下均无应变硬化发生，表现为近似的弹性-理想塑性变形行为。

图2f中材料在16000s－1应变率时出现明显软化。材料的这种应变硬化行为随应变率升高而降低的现象与高应变率下塑性变形的绝热效应有关。在动态压缩时，由于加载时间很短，材料塑性变形引起的热来不及散出，导致变形时的温度随应变水平的增加逐渐升高。较大的绝热温升引起材料软化就会导致应变硬化率降低，甚至出现应变软化。

高应变率变形时的绝热温升ΔT由变形过程中的塑形功转化成的热量产生，一般可由下式计算［12］:

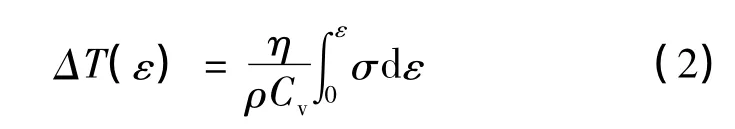
式中，σ为真实应力，ε为真实应变，ρ是材料密度，CV是材料的比热容;η是功热转化系数，通常，可认为塑性功全部转化成热量，取η=1.0。本研究所用材料，ρ=7.8 ×103kg/m3，CV=0.5kJ/(kgK) 。

图3给出了流动应力与绝热温度的对应关系。由图中可看出，材料温度随变形量的增大不断升高，这是动态加载时塑性变形产生的热在材料内不断累积的表现。而温度的升高通常会引起材料变软，因此在高应变率下变形时，实际上存在着材料本身的应变硬化与绝热效应引起的应变软化相互竞争。在1100s－1、室温变形至应变 0.12 时，绝热温升仅为44.5℃ ，由此引起的热软化较弱，因此应力-应变曲线仍表现出一定的应变硬化现象。而随着应变率的升高，由于材料的流动应力增大，变形时的塑性功增大，引起的绝热温升也显著增大，引起热软化增强，导致材料应变硬化率显著降低，甚至出现应变软化。例如，在16000s－1应变率下该现象最为显著，应变由0.1增至0.4的过程中，温度升高了138℃ ，流动应力下降107MPa。但随着试验温度的增高，材料流动应力降低，变形时的塑性功减小，引起的绝热温升降低，材料的软化现象也趋于不明显。例如在16000s－1应变率下，800℃ 应变达0.4时，绝热温升仅为70.1℃ ，材料表现出一定的应变硬化行为。

2.2 材料的温度效应

金属材料的塑性流动基本上是由位错的运动引起的［13］。根据热激活位错运动理论［12］，位错运动过程需克服的能量势垒有短程和长程两种。其中短程势垒为热激活项，可由热能ΔG克服;长程势垒则由材料结构本身决定。因此，材料的流动应力可表示为热激活σ*和非热激活σG两部分，即

热能ΔG与温度及应变率存在以下关系［12］:

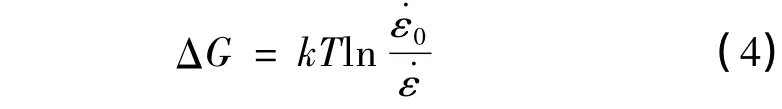
假设势垒为简单的矩形形式时，σ*可表示为［12］

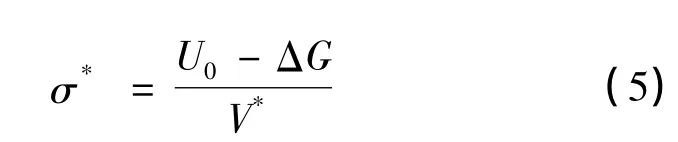
式中，U0为温度0K时对应的短程势垒(J)，k为Boltzmann量，T为热力学温度(K)，为参考应变率。V*为激活体积(m3)，与林位错间距、位错扩展宽度和Burgers矢量有关。V*可由式对ln˙ε求偏导得到，即:

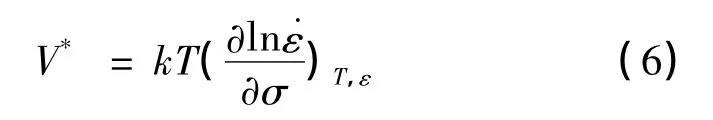
表1给出了无量纲激活体积随温度的变化趋势，其中 b=2.65 × 10－10m，为 Burgers矢量的模［14］。由表1可以看出，激活体积随温度升高不断增加。这是由于随着温度升高，原子振荡的幅度加大导致热激活体积增大。温度升高时，ΔG增加，短程势垒的有效高度降低［12］，位错运动克服势垒所需应力减小，因此式5中σ*为温度的减函数;而非热激活 (长程)势垒项σG几乎不随温度变化。宏观上即表现为图2中相同加载速率下材料的流动应力随着温度升高而迅速降低。

表1 激活体积V*随温度的变化(ε=0.10)Table 1 activation volume V*at different temperature

材料流动应力对温度变化的依赖性可采用温度敏感性因子定量分析。本文参考Morrone等给出的定义［15］，温度敏感性因子 ST为:

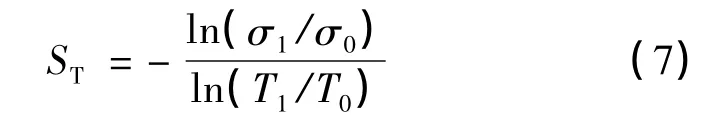
式中T0为参考温度(本工作中取20℃)，T1是实验温度，σ0和σ1分别是T0和T1时对应的流动应力(本工作中取真实应变为0.1时的应力)。

图4 温度敏感性因子随应变率的变化(ε=0.1)Fig.4 Variation of temperature sensitivity as a function of strain rate at a constant strain of 0.1

图4给出了不同温度下材料的温度敏感性因子随应变率的变化。由图中可以看出，随着应变率的升高，低温时温度敏感性因子变化不大;温度超过600℃，温度敏感性因子呈减小趋势。同一应变率下，温度敏感性因子则随着温度的升高显著增大，且高温时增大趋势更为明显。

2.3 材料的应变率效应

将图2中不同应变率下结果进行比较可发现，本研究不锈钢材料具有明显的应变率强化效应。这是由于随着应变率的增加，位错克服势垒所需的时间减少，同时热能ΔG的作用也会有所下降［12］。因此高应变率变形会导致势垒有效高度升高，宏观上即表现为材料的变率强化效应。这一现象在应变率的对数坐标下更为明显。图5给出了真实应变0.1时不同温度下材料流动应力随应变率的变化规律。由图可知，材料在各温度下的流动应力均随应变率的增加而增加。而且材料在室温准静态的流动应力明显高于800℃，16000s－1时的流动应力，表明该不锈钢材料的应变率效应相对温度效应较弱。

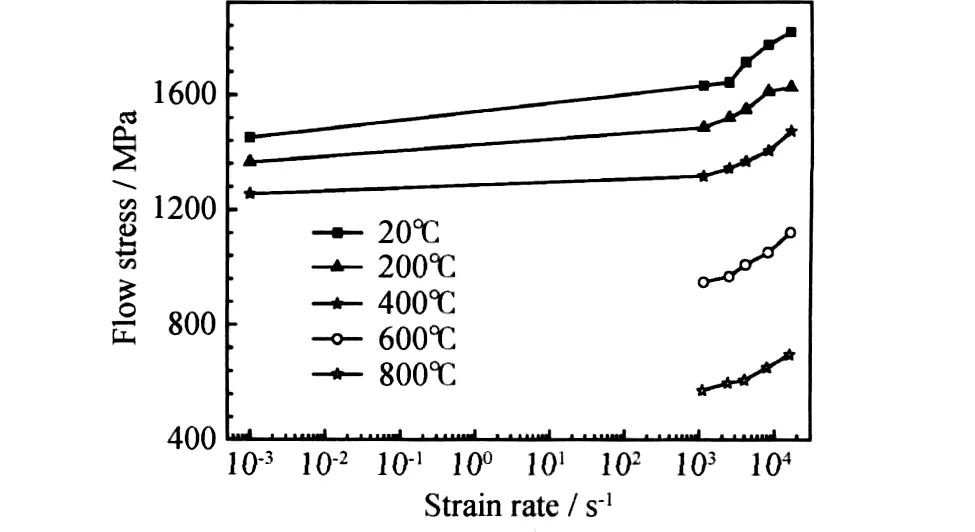
图5 应变为0.1时不同温度下流动应力-应变率曲线Fig.5 Influence of temperature on flow stress at a constant strain of 0.1，as a function of strain rate

为了定量的描述材料的流动应力对应变率的依赖性，将双对数坐标下应力-应变率曲线的斜率定义为应变率敏感性因子［15］m:

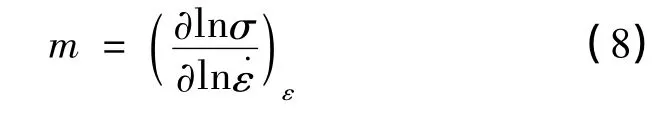
式中m的取值与应变大小有关，本研究用中取真实应变为0.1时的流动应力来计算应变率敏感性因子。表2给出了由式8计算得到的不同温度下的应变率敏感性因子。可以看到，温度在200～400℃间变化时，材料的应变率敏感性因子变化不大，高于600℃应变率敏感因子明显增加，表明该不锈钢材料在高温变形时对应变率更为敏感。

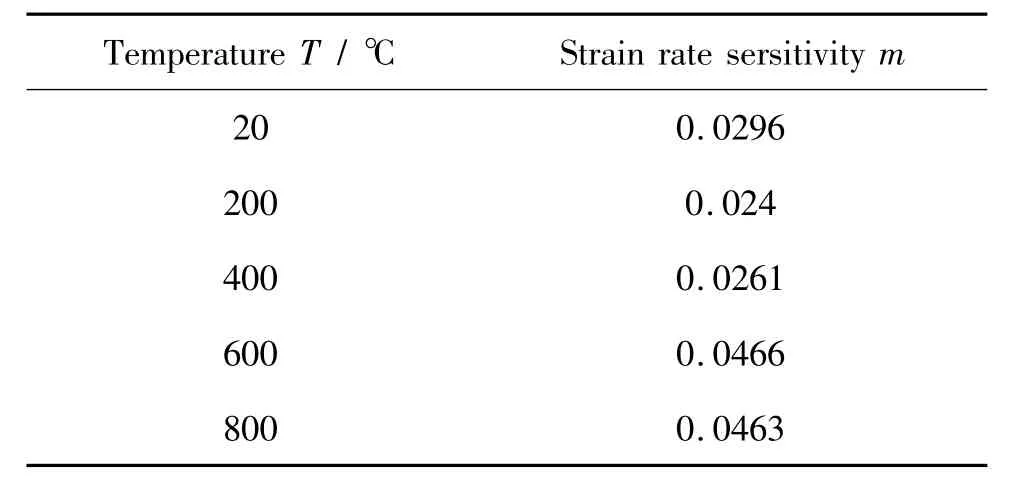
表2 不同温度下的应变率敏感性因子(ε=0.1)Table 2 Strain rate sensitivity at different temperature( ε =0.1)

3 结论

在较大的温度和应变率范围内研究了不锈钢材料的动态压缩力学行为，得到如下结论:

(1)准静态及较低应变率下该材料表现出微弱的应变硬化现象。高应变率下变形时，由于材料本身的应变硬化与绝热效应引起的应变软化相互竞争，材料在部分温度下表现为应变软化。

(2)该不锈钢材料具有较显著的温度敏感性，温度敏感性因子随着温度的升高显著增大，高温时温度敏感性随应变率增加而减小。

(3)材料具有应变率强化效应，高温、高应变率下材料力学性能对应变率更加敏感。

［1］LEE WS，LIN C F，LIU T J.Strain rate dependence of impact properties of sintered 316L stainless steel［J］.Journal of Nuclear Materials 2006，359(3):247 －257.

［2］GUO W G，SIA Nemat Nasser.Flow stress of nitronic-50 stainless steel over a wide range of strain rates and temperatures［J］.Mechanics of Materials 2006，38(11):1090 －1103.

［3］LEE W S，LIU C Y.The effects of temperature and strain rate on the dynamic flow behaviour of different steels［J］.Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing，2006，426(1 －2):101—113.

［4］王艳，王明家，蔡大勇，等.高强度奥氏体不锈钢的热变形行为及其热加工图［J］.材料热处理学报，2005，26(4):65－68

［5］罗德信，曾萍.马氏体不锈钢高温变形抗力研究［J］.轧钢，1995，6:12 －14.

［6］童骏，傅万堂，林刚，等.00Cr25Ni7Mo4N超级双相不锈钢的高温变形行为［J］.钢铁研究学报，2007，19(10):40－43.

［7］何著，赵寿根，杨嘉陵，等.0Cr17Ni4Cu4Nb不锈钢动态力学性能研究［J］.材料科学与工程学报，2007，25(3):418－421.

［8］李玉龙，郭伟国.微型 Hopkinson杆技术［J］.爆炸与冲击，2006，25(6):303 －308.

［9］李玉龙，索涛，郭伟国，等.确定材料在高温高应变率下动态性能的Hopkinson杆系统［J］.爆炸与冲击，2005，25(6):487－492.

［10］LI Y L，GUO Y Z，HU H T，et al.A critical assessment of high-temperature dynamic mechanical testing of metals.［J］.International Journal of Impact Engineering，2009，36(2):177－184.

［11］郭伟国，李玉龙，索涛.应力波基础简明教程［M］.西安:西北工业大学出版社，2007.

［12］Meyers M A.材料的动力学行为［M］.张庆明，刘彦，黄风雷，等，译.北京:国防工业出版社，2006.

［13］许泽建，李玉龙，刘明爽，等.不锈钢0Cr18Ni10Ti焊接头高温、高应变率下的动态力学性能［J］.金属学报，2008，44(1):98－104.

［14］XU Z ，LI Y.Dynamic behaviors of 0Cr18Ni10Ti stainless steel welded joints at elevated temperatures and high strain rates［J］.Mechanics of Materials，2009，41:121 – 130.

［15］MORRONE A A.Strain rate and temperature effects during dynamic deformation of polycrystalline and monicrystalline high purity aluminum including TEM studies［D］.Providence，USA，Brown University，1986.