多肋T形梁桥动力反应的分析

甘亚南，荀 勇，周广春

((1.盐城工学院 土木工程学院，江苏 盐城 224051;2.哈尔滨工业大学 土木工程学院，哈尔滨 150090)

多肋T形梁桥在制造、结构性能和外观上的许多优点，常用于中等跨径的钢筋混凝土或预应力混凝土铁路及公路桥梁中［1－3］。但因剪力滞后效应的影响［4－7］，该类结构受力非常复杂。在对多肋T形梁桥的力学分析中，国内外学者进行过探索，均未同时考虑铁木辛柯剪切变形、剪力滞后效应和剪滞翘曲应力自平衡条件的影响，因而其力学分析具有一定局限性。特别是动力分析中多肋T形梁桥受剪力滞后效应的影响，其主振型的正交性难以把握，经典强迫振动理论已不适用，动力学分析难度加大［8－9］。本文考虑剪滞翘曲应力的自平衡条件，且对多肋T形梁上翼板和悬臂翼板设置不同的剪滞纵向动位移差函数，运用直接解法对多肋T形梁桥的动力反应进行分析，揭示多肋T形截面梁动力反应规律及各参数之间的内在关系。

1 多肋T形梁动力学特性分析

1.1 考虑剪滞翘曲应力自平衡条件，多肋T形梁的控

制微分方程和自然边界条件

1.1.1 体系总势能

图1为动载荷(图2)作用下多肋T形截面梁，若结构跨度为L，在对称弯曲状态下，截面上的竖向动挠度为w(z，t)，竖向动转角为 θ(z，t)，由剪滞效应引起的翼板动位移为u1(z，t)，u2(z，t)，…，un(z，t)，即翼板动位移为由剪滞效应引起多肋T形截面梁翼板的翘曲位移［3－4］和服从平面假设刚性截面均匀位移wso1U1(z，t)，…，wsomUm(z，t)，…，wsonUn(z，t)之和，可表示为［3］:

悬臂板［10－11］:

式中:wsy1(x)为多肋T形梁悬臂板的不均匀分布函数。且wsy1(x)的形函数如图2所示，当采用图2所示的坐标轴 ξ，wsy1(x)=wsy1(ξ)［10］。

上翼板(如图1，第m部分):

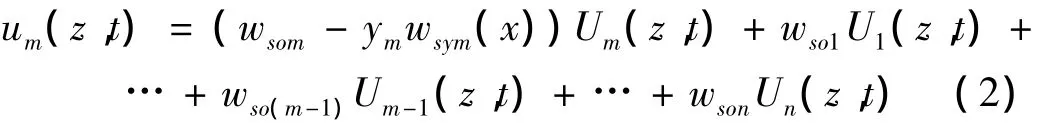
同样可得:

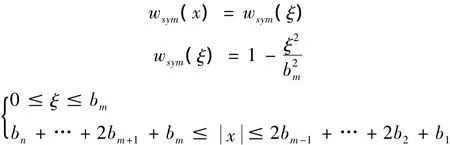
由剪滞效应产生的正应力和剪应力分别为:

悬臂板:

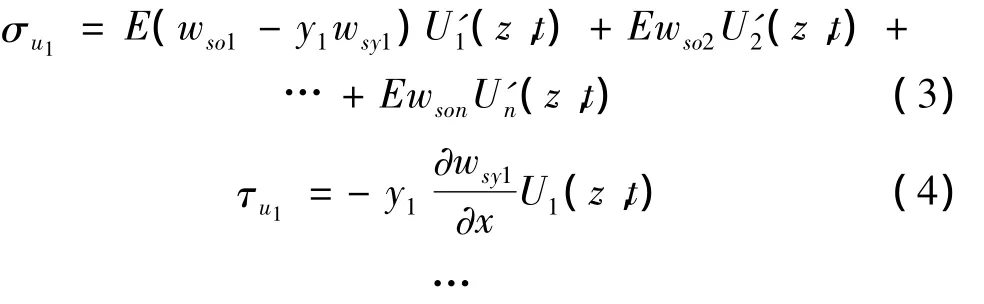
上翼板(第m部分):

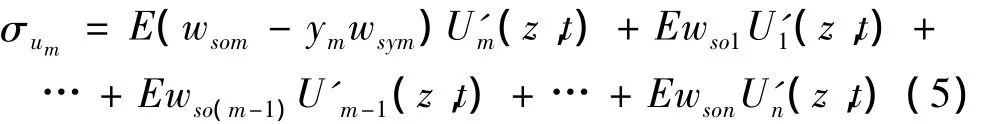
图1 多肋T形梁截面(i=1，2，…，m，…，n)Fig.1 Cross section of T － beam with multi－ ribbed slabs(i=1，2，…，m，…，n)

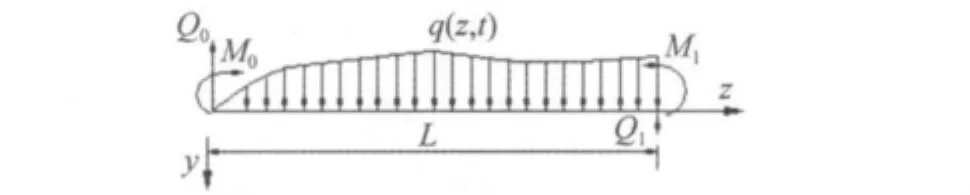
图2 坐标及动荷载系统Fig.2 Coordinate and dynamic load system

那么，翼板总应力为:

悬臂板:

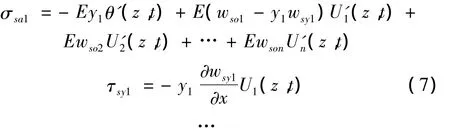
上翼板(第m部分):

腹板:

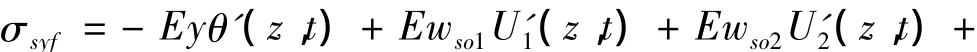
式中“'”表示对坐标z求偏导数。wso1，wso2，wso3，…，wson分别为悬臂板、上翼板满足自平衡条件求得的常数，即:

由∫AE(wso1－y1wsy1)U'1(z，t)dA=0，可得:

由∫AE(wsom－ymwsym)U'm(z，t)dA=0，可得:

多肋T形梁各项变形势能为

(1)悬臂板与上翼板

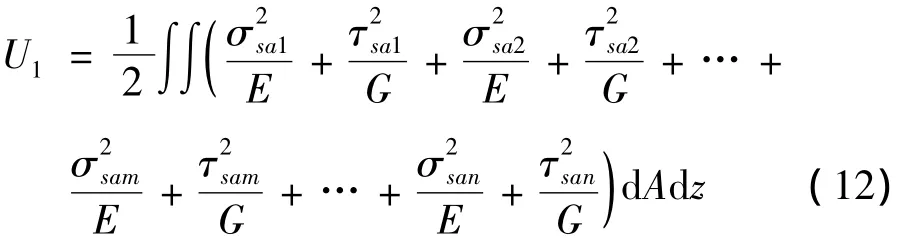
(2)腹板

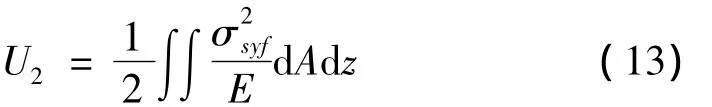
(3)剪切应变能

(4)多肋T形截面梁荷载势能Up:

系统总势能为:

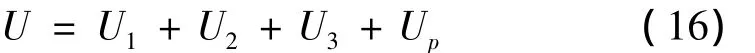
结构总动能T为［8－9］:

1.1.2 多肋T形梁微分方程及自然边界条件

式中:U1(z，t)为剪力滞后效应引起梁悬臂板纵向动位移差函数;Um(z，t)为剪力滞后效应引起梁上翼板第m部分纵向动位移差函数;M11(z，t)为悬臂板剪滞效应产生的关于x轴动弯矩;M1m(z，t)为梁上翼板第m部分剪滞效应产生的关于x轴动弯矩;MzA(z，t)为梁段端产生竖向动转角 θ(z，t)的关于x轴动弯矩;Q(z，t)，q(z，t)为梁端竖向剪力与截面上竖向分布力;E，G为材料的杨氏模量和剪切模量;A1为梁悬臂板截面面积;Am为梁上翼板第m部分面积;AN为梁腹板面积;A为梁全截面面积;k为截面形状系数;I1为悬臂板关于x轴的惯性矩;Im为梁上翼板第m部分关于x轴的惯性矩，且I=I1+I2+…+Im+…+In。

1.2 n=1时，多肋T形梁动力学特性研究

图3所示以n=1时多肋T形梁的动力学特性为研究对象，其结果依然对n为任意值的多肋T形梁的动力学特性具有指导意义。分析过程如下:

图3 多肋T形梁截面(n=1)Fig.3 Cross section of T-beam with multi-ribbed slabs(n=1)

1.2.1n=1时多肋T形梁微分方程和自然边界条件为

计算得:

1.2.2n=1时多肋T形梁微分方程求解

若多肋T形梁强迫振动频率为ω，则令:

由式(20)可得U1的导数表达式，将其代入式(18)得:

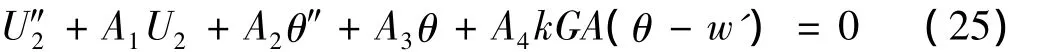
式中:

同样将U1的导数式代入式(19)的二次求导式可以得到:

通过式(25)和式(26)之间的代换消去U2项，然后将式(21)代入该新微分方程消去θ项，最后可得新微分方程为:

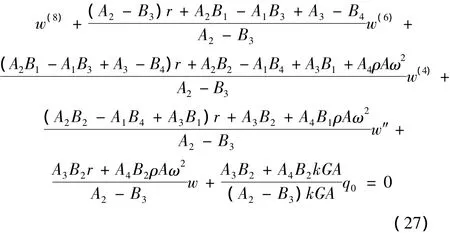
式中:r=(ρω2)/(kG)。

对式(27)分析可知，其微分方程特征解为:

则方程w(z)的解为:

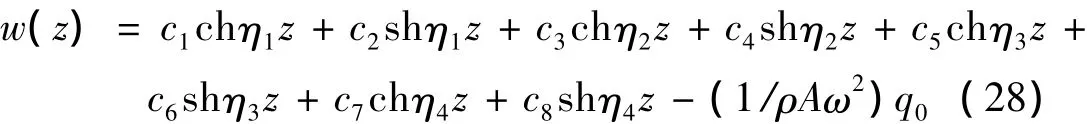
式中:

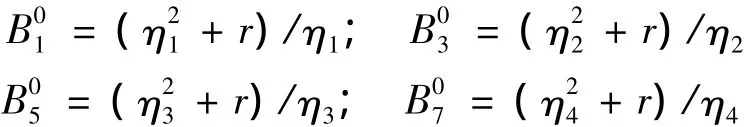
根据常微分方程组性质和方程(29)解的形式假设U1(z)，U2(z)解的形式为:

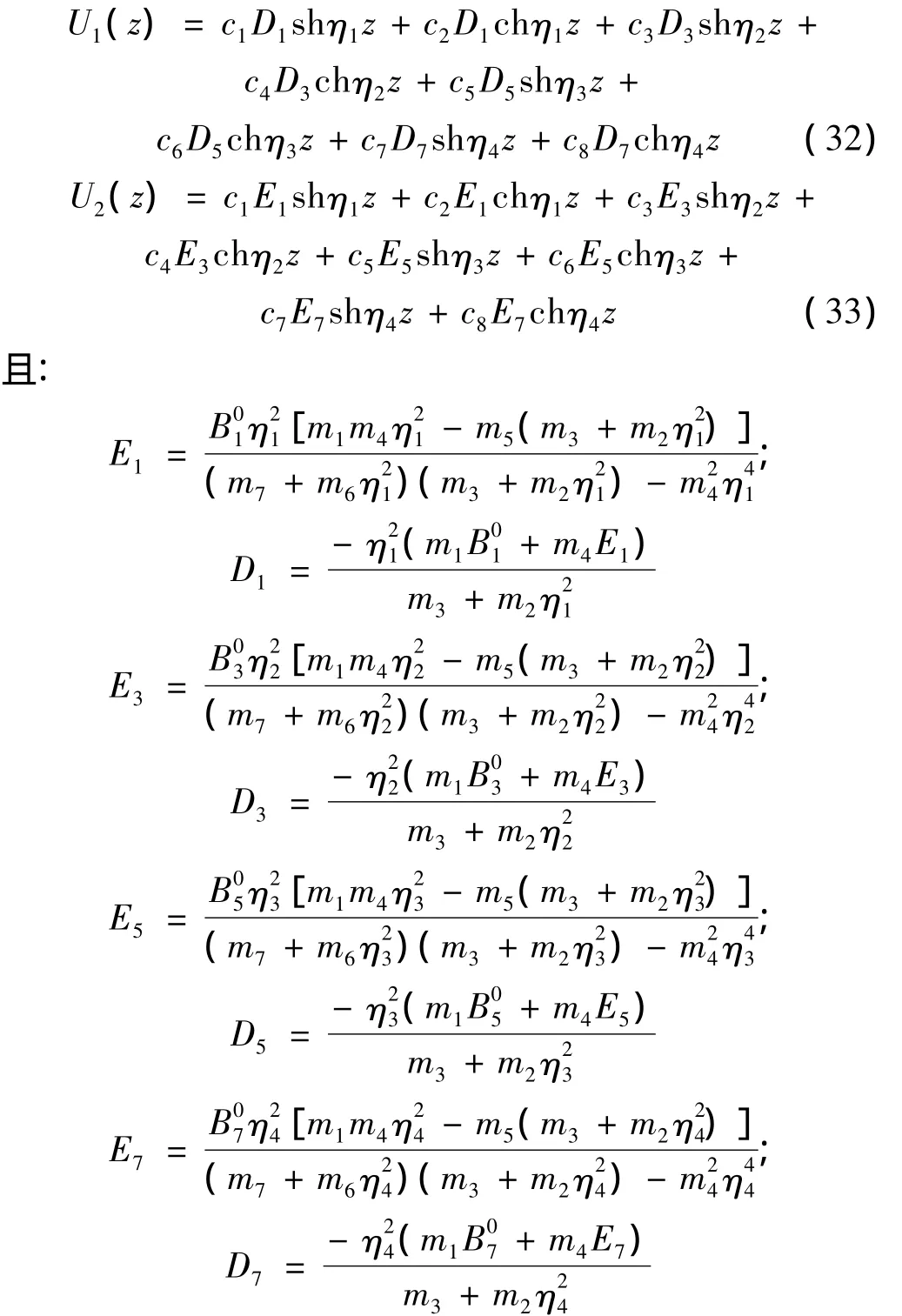
2 几种常用自然边界条件(n=1)

(1)悬臂多肋T形梁几何、物理边界条件为:

(2)简支多肋T形梁几何、物理边界条件为:

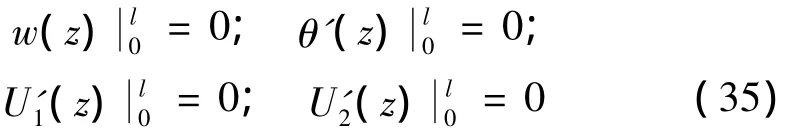
对于图4所示简支多肋T形梁，若跨间所受力为一个或多个集中力，且集中力pk左右相邻边界距离为Lk1和Lk2，则k点处须引入下列连续边界条件为:

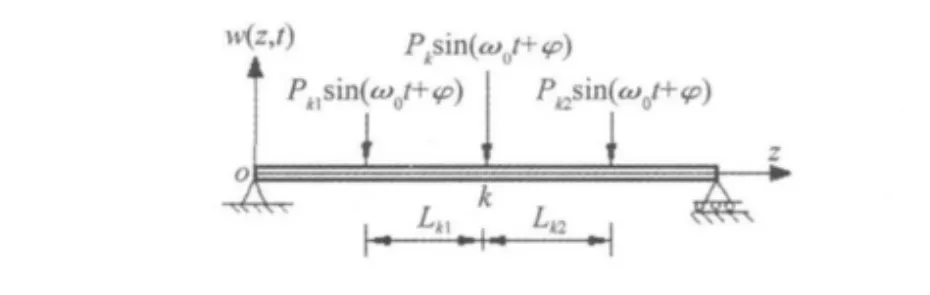
图4 算例中坐标系的约定Fig.4 The fixed coordinate system in the calculation example

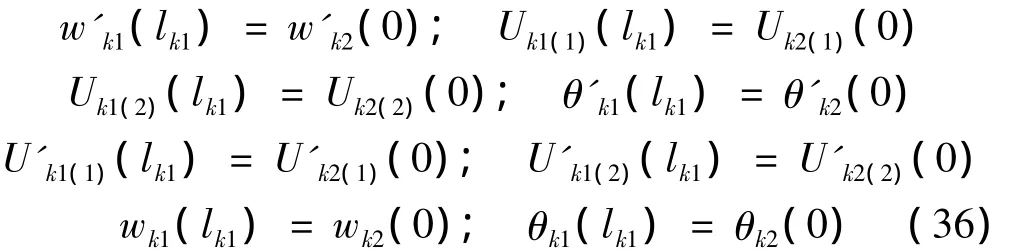
3 算例

对于多肋T形梁，其材料参数和几何参数为E=3.5 ×104MPa;G=1.5 ×104MPa;t1=0.3 m;ρ=2 500 kg/m3;t2=0.3 m;tw1=0.25 m;b1=1.625 m;b2=3.125 m，梁高h=1.5 m，力学分析中简谐集中力为P(z，t)=98 000sin(ω0t+φ)，力的作用点为梁纵向和横向中线的交点。根据本文推导公式和其它算法可计算出梁的自振频率及动力反应幅值。(注:ANSYS有限元法计算中，按图3多肋T形梁各交点坐标绘制出该多肋T形梁截面，然后应用ANSYS有限元的Extrude功能形成体，划分实体单元网格后，模拟简支边界条件在多肋T形梁一端节点x，y，z三向施以约束，另一端则在节点x，y方向施以约束)。

在对梁自振频率的求解过程中，令均布简谐力q(z，t)=0，应用MATLAB软件与边界条件式(35)便可得梁的自振频率值如表1。

表1数据表明:

铁木辛柯梁理论自振频率计算值大于传统理论值，而传统理论值又大于本文理论值。基于最小势能原理可以判断传统算法优于铁木辛柯梁理论，而本文算法又优于传统算法，因而多肋T形梁动力反应分析中自平衡条件的引入有其理论依据。

表1 简支多肋T形梁的固有频率值(单位:Hz)Tab.1 Natural frequency of simply-supported T-beam with multi-ribbed slabs(unit:Hz)

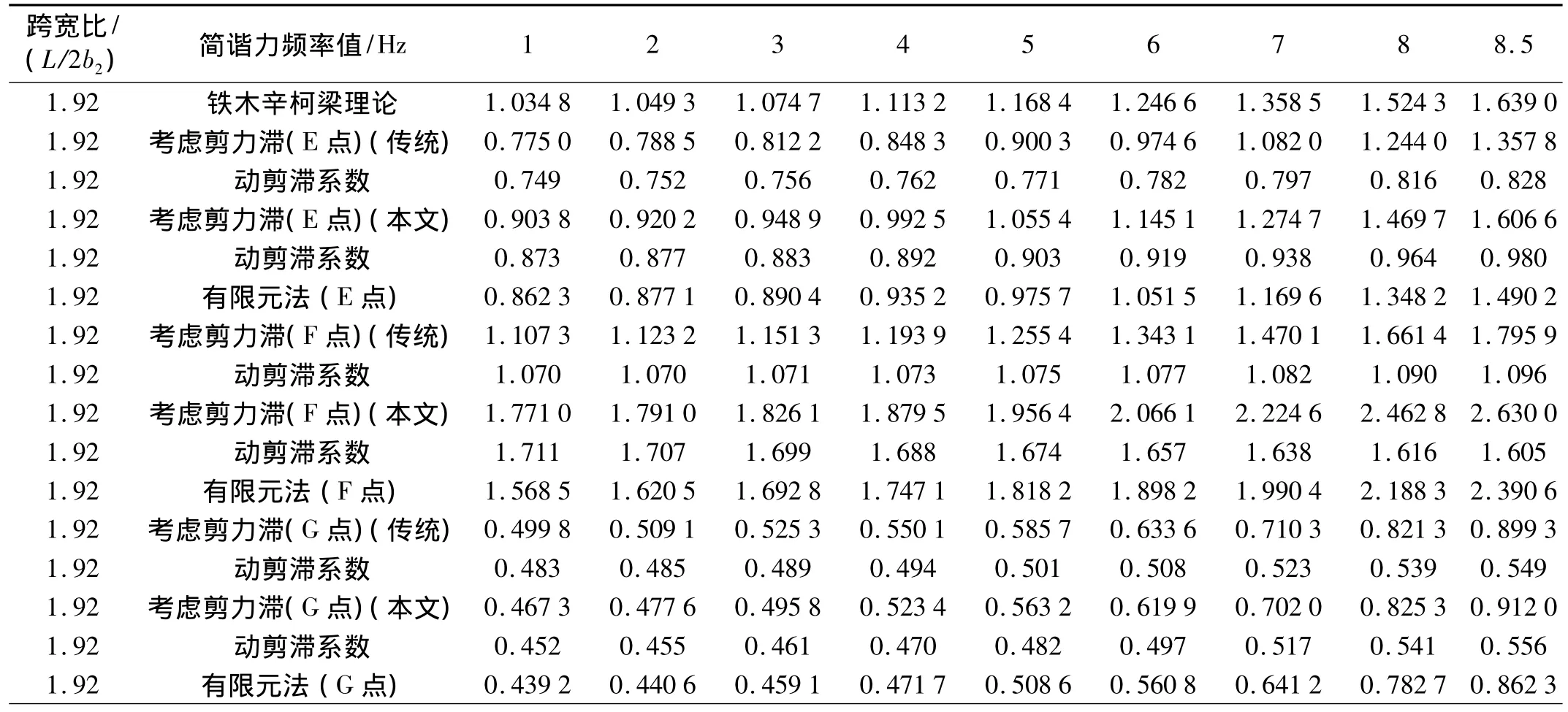
表2 简支多肋T形梁E、F和G点的动应力幅值 (单位:104Pa)Tab.2 Dynamic stress amplitude of simply-supported T-beam with multi-ribbed slabs located at the crossing points E，F and G(unit:104Pa)

注:表2动剪滞系数(λD=多肋T形梁翼板剪滞理论动应力幅值(σJD)/多肋T形梁翼板铁木辛柯梁理论动应力幅值(σDT)

表2和图6说明:

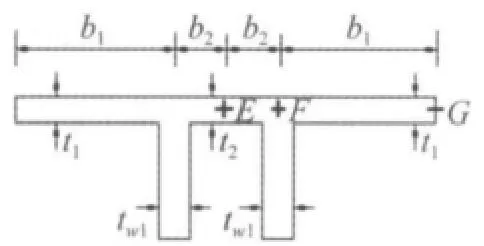
图5 交点E、F和G为所求多肋T形梁动应力幅值位置Fig.5 Dynamic stress amplitude of the T-beam with multi-ribbed slabs located at the crossing points E，F and G

① 尽 管 多肋T形梁桥传统理论自振频率计算值与本文理论值差别很小，但动力反应分析中E、F和G点两种理论的动应力幅值皆有较大差异，且F点的差异更大，因而在多肋T形梁桥的动力分析中，自平衡条件的引入十分必要;②简谐力的频率值对多肋T形梁桥动剪滞系数有一定影响，而接近共振点动剪滞系数的差异主要来自铁木辛柯梁理论共振点与传统和本文理论共振点的差异，算例表明，多肋T形梁动力反应分析中剪滞效应与自平衡条件的影响不可忽视。

图6 简支多肋T形梁跨中F点动应力幅值比较图(z=L/2，L=12 m)(简谐集中荷载)Fig.6 The Comparison of dynamic stress amplitude of middle-span of simply supported T-beam with multi-ribbed slabs located at the crossing point F(z=L/2，L=12 m)(harmonic concentrated load)

4 结论

多肋T形梁自平衡条件及多个纵向翘曲动位移差函数(U1(x，t)，U2(x，t)，…，Un(x，t)，)的设置，更加准确反映了该类结构翼板的剪滞变化幅度，因而本文理论提高了多肋T形梁动力反应的计算精度，为该类结构的动力反应从定性到定量分析奠定了基础，同时对多肋T形梁桥抗风、抗震有一定借鉴意义，所得公式丰富和发展了剪滞理论。

［1］王荣辉，周建春.斜交多肋T梁桥空间计算的有限元单元法［J］.工程力学，2003，20(1):163 －167.

［2］王荣辉，夏锦红，王玮祎.板肋式多肋T梁桥的空间分析［J］.华南理工大学学报(自然科学版)，2003，31(2):56－61.

［3］张元海，李 乔.宽翼缘T梁剪滞效应分析的改进方法［J］.兰州交通大学学报，2004，23(3):94 －97.

［4］Song Q G，Sordelis A C.Shear lag analysis of T，I and box beams［J］.Structural Engineering，1990，116(5):1306－1318.

［5］周 坚，涂令康.再论槽型梁的剪力滞［J］.工程力学，1994，12(2):65 －75.

［6］ Foutch D A，Chang P C.A shear Lag anomaly［J］.J Struct Engrg，ASCE，1982，108(7):1653 －1658.

［7］Chang S T.Prestress influence on shear lag effect in continuous box girder bridge［J］.J Struct Engrg，ASCE，1992，118(11):3113 －3121.

［8］黄新艺，盛洪飞，陈彦江，等.薄壁箱梁桥动力特性分析的三梁式计算模型及试验研究［J］.振动与冲击，2008，27(12):40－43.

［9］克拉夫 R.结构动力学［M］.王光远，等译.高等教育出版社，2006，11.

［10］吴亚平，赖远明，朱元林，等.考虑剪滞效应的薄壁曲梁有限单元法［J］.工程力学，2002，19(4):85 －89.

［11］甘亚南，周广春.薄壁箱梁纵向剪滞翘曲函数精度选择的研究［J］.工程力学，2008，25(6):100 －106.

［12］胡海昌.弹性力学的变分原理及其应用［M］.北京:科学出版社，1981.