基于LMD的时频分析方法及其机械故障诊断应用研究

王衍学，何正嘉，訾艳阳，袁 静

(1.桂林电子科技大学 机电工程学院，桂林 541004;2.西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

机械设备状态监测与故障诊断是保证设备高效运行、提高企业经济效益、维护公共安全具有重要的现实意义。振动信号分析是目前普遍采用的一种机械故障诊断方法。机械设备振动信号通常蕴含着丰富的故障特征信息。当机械设备发生碰摩、冲击等故障时，系统的阻尼、刚度、弹性力等都发生变化，呈现出非线性、振动信号变得非平稳［1］。因此，如何有效地从振动信号中提取有用信息成分是机械设备故障诊断研究的关键。机械故障领域学者一直以来也都在寻找一些有效的信号处理与特征提取方法。迄今，机械振动信号的常见处理方法有时域分析法、频域分析法和时频域分析方法(短时傅里叶变换、Wigner-Ville分布、小波分析、Hilbert-Huang transform等)。每种方法都有其优势与不足，而时频域分析方法由于能够综合反映信号信息成分而得到广泛应用。

Smith［2］提出一种新的信号分解方法—局部均值分解(Local mean decomposition，LMD)。LMD自适应地将信号分解为若干个乘积函数(Product Function，PF)之和，其中每一个PF可看作由一个包络信号与一个纯调频信号的乘积得到。目前国内外学者对于LMD算法的研究以及其在机械非平稳、非线性信号分析中的应用尚处于起步阶段，诸多问题尚需解决。本文基于LMD的瞬时频率精确计算、瞬时时频构建技术及其故障诊断的应用研究，并成功应用于转子碰摩故障、实际轧机齿轮箱齿面剥落故障诊断。

1 局部均值分解原理

LMD方法将信号自适应地分解为一系列PFs，每一PF是一个包络信号和一个纯调频信号的乘积得到。LMD分解具体算法步骤如下:

(1)首先确定原始信号x(t)所有局部极值点(包括极大值点与极小值点)n11(kl)(l=1，2，…，M)，分别由式(1)与式(2)求得局部幅值m11(t)与局部均值a11(t)。

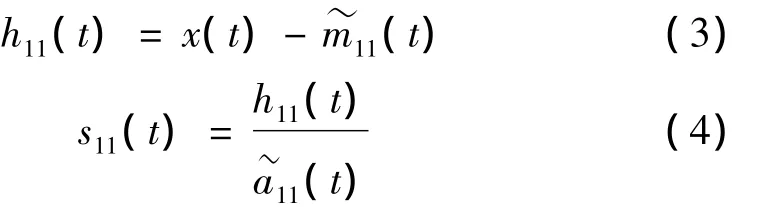
(3)若s11(t)不是一个区间［－1，1］上的纯调频信号，则将s11(t)作为原始信号重复n次(1)与(2)的操作，直到满足要求为止。瞬时相位(Instantaneous Phase，IP)与瞬时频率(Instantaneous Frequency，IF)可由式(5)与式(6)分别得出:

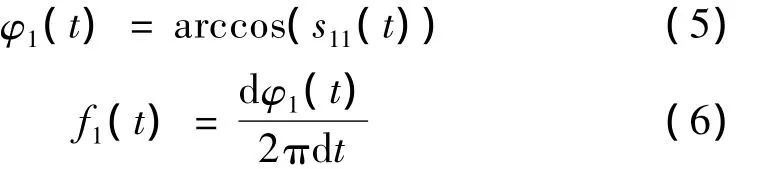
(4)所有局部幅值的乘积得到瞬时幅值(Instantaneous amplitude，IA)成分:

而首个乘积函数可由下式得到:

(5)将第一个PF分量从原始信号中分离出来，

得到新的信号u1(t)作为原始信号重复上述(1)～(4)步骤k次，直到uk(t)为单调函数。至此，原始信号可表示为k个PF分量与一个单调分量的和:

LMD算法与EMD有诸多相似之处，如LMD同样需要进行端点处理，本文作者在文献［3］中提出一种端点效应处理方式。此外，对于LMD与EMD的异同，作者进行了对比研究，详见文献［4］。

2 LMD的时频分析技术

时频分析方法能同时提供信号在时域与频域的局部化信息。LMD时频谱构建的前提是准确计算IA与IF。每一分量的IA是由公式(7)得到，而准确的IF求解并不容易。本文将提出一种改进的瞬时频率求解方法。

2.1 瞬时频率求解

如前所述，LMD采用式(5)与式(6)求信号的瞬时相位与瞬时频率，因此瞬时频率的求解过程与信号的LMD分解过程是一步完成的。另外，可以看出LMD求解瞬时频率是不依靠Hilbert变换，因此也就不存在Hilbert变换端点效应问题，这相比Hilbert-Huang变换方法已经有了一定改进。Huang等［5］也意识到Hilbert变换求解瞬时频率的缺点，提出了一种经验AM/FM分析方法，具体操作过程为对于某个IMF成分x(t)，采用三次样条函数求其极大值包络线e1(t)，利用下式对其进行标准化处理:

信号的瞬时相位与瞬时频率同样采用式(5)、式(6)求得。不难看出，这种经验AM/FM的瞬时幅值与瞬时频率的求解方法本质上非常类似于LMD方法，即两者均是通过迭代归一化操作得到一个纯调频信号。式(5)计算得出某一个相位φi(t)是一个幅度在［0，π］之间波动函数，因此需要进行解卷，具体解卷过程可用下式表示:

瞬时频率是由每一分量“解卷”后的瞬时相位的一阶导数求得，但是直接求导在两端的精度并不高，因此实际的求导操作可以借鉴文献［6］中的数值运算方法，这种方法的一大优点是可以很好解决瞬时相位在边界上的求导问题。例如在信号左端点处，采用信号左端点处五点求导公式为:

而在信号右端点可以采用类似处理:

一般的情况下求导过程可以用下式计算:

为对比瞬时频率的求解精度，模拟一个调频Duffing信号，该信号精确的瞬时频率如图1(a)。图1(b)为采用本文提出的瞬时频率计算结果，可以看出结果与精确数值很接近;图1(c)与图1(d)为采用原始LMD与Hilbert-Huang transform所计算的结果，不难看出两者均存在较大的误差。本文改进瞬时频率求解方法实际也可用于计算基于经验AM/FM分析方法的瞬时频率。

2.2 瞬时时频谱构造

EMD分解得到一系列IMF后，可通过Hilbert变换构造信号的Hilbert时频谱。EMD分解与Hilbert变换的结合称为HHT［7］。当准确的瞬时幅值与瞬时频率均已求得，LMD同样可以构造出信号的时频能量分布图。由于在此构造过程未采用Hilbert变换，因此与HHT不同，我们称之为瞬时时频谱(Instantaneous Time-Frequency Spectrum，ITFS)［3］。ITFS 具体构造方法可用下式表示:

图1 瞬时频率计算比较Fig.1 Comparison of the Computed of IFs

若HHT方法采用1.3节中介绍的经验AM/FM方法计算IA与IF，则信号的时频结构同样可由式(19)构建。ITFS综合反映了信号经LMD分解后所提取的信息成分，因此后续的应用中我们主要依靠ITFS进行分析。

3 应用研究

3.1 转子碰摩故障诊断

碰摩故障是一种复杂非线性故障，之前大量的研究为转子碰摩故障提供依据。当碰摩故障发生，将会出现X/3、X/2 等分数谐波成分［8－9］。在 Bently转子实验台上，设定转子以2 230 r/min的恒定速度转动(工频约为37 Hz)，采用电涡流传感器采集转子轻微碰摩时的振动位移信号，采样频率为2 000 Hz，采样点数为1 024。图2显示轻微碰摩故障信号及其频谱，从图中不难发现信号中除了基本工频成分外，没有其他任何有意义的成分存在。

采用LMD技术对振动信号进行分解，图3为LMD分解得到的ITFS。图3中虚线圈中的即为提取的转子工频成分，可以看出该成分是在工频37 Hz附近上下波动。此处工频波动的原因可以解释为转子在运动过程中受到反向摩擦力作用，在碰摩瞬间影响转子的转动频率。另外，该波动工频曲线下面两条线条为表征转子碰摩故障存在的非线性次谐波(亚频)成分。因此，LMD的ITFS成功提取转子早期、微弱碰摩故障特征信息。

图2 早期摩擦信号及其频谱Fig.2 Signal of incipient rub fault and its spectrum

图3 早期摩擦信号LMD的ITFS分析分析Fig.3 ITFS of the incipient rub fault signal

3.2 轧机齿轮箱故障诊断

轧机是典型的低速变载设备，工作环境恶劣，其中关键部件减速齿轮箱极易损坏。此外，轧机设备的运转速度随着系统负载的变化而变化，因此对轧机的监测与诊断带来一定困难。本文采用LMD瞬时时频谱方法对某热轧厂精轧传动系统的主减速箱进行监测诊断。该齿轮箱为一级传动系统，传动比为2.954 5。齿轮箱中大、小齿轮均为斜齿轮，齿数分别为65、22，模数均为30。由于轧制过程中轧机的速度是在某个范围变动的，高速轴(输入轴)的转速约为3～4Hz。信号采样频率为2 560 Hz，采样点数为4 096。

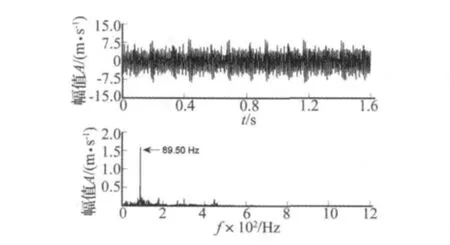
图4 轧机振动时域信号及其频谱分析Fig.4 Vibration signal acquired on a mill and its spectrum

图4为2008年4月9日在高速轴垂直方向采集的振动速度信号及其频谱，从频谱图中可很容易识别出一阶啮合频率为89.50 Hz，相应地高速轴转频约为4.068 Hz。众所周知，当齿轮箱中某个齿轮出现故障时会出现以啮合频率及其谐波为载波频率的幅值与相位调制现象。该种工况下信号的LMD瞬时时频谱如图5所示，图中白色点划线表示齿轮基本啮合频率。由此啮合频率即可计算出小齿轮所在高速轴转频，结果约为4.068 Hz(周期约为0.245 8 s)。另外，在信号的ITFS谱中200～400 Hz频带区域内发现存在周期约为0.246 2 s的冲击成分(如图5的黑色虚线圈中所示)恰好与高速轴的转频一致。据此，可推断出高速轴小齿轮存在局部故障。

图5 轧机振动信号LMD的ITFS分析Fig.5 ITFS of the mill vibration signal using LMD

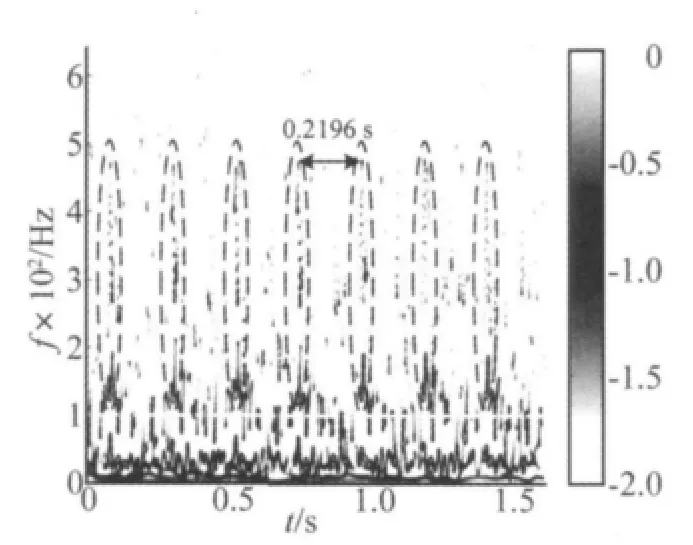
图6 轧机严重故障信号LMD的ITFS分析Fig.6 ITFS of the signal acquired as mill with severe fault

图7 轧机齿轮箱高速轴齿轮齿面损伤图Fig.7 The picture of the local scuffing damage in pinion

图8 轧机齿轮箱更换损伤齿轮后ITFSFig.8 ITFS of signal acquired after the damaged pinion is replaced

此外，需要特别指出的是LMD的ITFS中故障引起的冲击成分所处频带范围与部件故障的严重程度有关，频带范围越宽表征故障越严重。原因是当故障严重程度增加，时域冲击能量表现更为集中和短暂，根据测不准原理其相应频带范围将变宽。为了说明这一点，图6给出了轧机2008年4月16日同一测点采集振动信号的ITFS。从图中可以看出明显的间隔为0.219 6 s冲击故障特征成分。此时啮合频率(如图6中白色点划线)为100.6 Hz，据此可知高速轴的转频为4.573 Hz(周期约为0.218 7 s)。易知，故障仍然是与高速轴小齿轮有关。此外，图6中所表征的冲击成分所处频带范围扩大到约为125～500 Hz，已超过图5中冲击成分带宽，表明小齿轮局部故障已经恶化。随即于2008年4月17日开机检查，发现高速轴齿轮齿面发生严重剥落，如图7所示。这一结果也进一步证实了LMD时频分析技术可以有效诊断出早期的齿轮局部故障。由于发现及时小齿轮尚未对低速轴大齿轮产生影响，立即更换高速轴小齿轮。图8为2008年4月18日采集振动信号的ITFS，从中发现只有啮合频率及其谐波以及随机成分存在，无周期性冲击成分，易知故障已经排除，设备处于正常运行状态。

4 结论

本文研究LMD的IF精确求解以及ITFS构建理论，得出主要结论如下:

(1)LMD瞬时频率求解与信号分解是一体化完成的，且求解过程中完全脱离Hilbert变换。采用本文的方式计算信号瞬时频率，可提高求解精度。

(2)由IF与IA构造的ITFS能全面反映信号特征信息，如碰摩故障的微弱工频波动性与非线性次谐波成分，低速变载轧机早期齿轮局部故障诊断及其严重程度识别等。因此，LMD为机械系统状态监测与早期微弱故障检测方提供一个有效方法。

［1］何正嘉，訾艳阳，孟庆丰，等.机械设备非平稳信号的故障诊断原理及应用［J］.北京:高等教育出版社，2001.

［2］ Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，(2):443 －454.

［3］ Wang Y X，He Z J，Zi Y Y.A demodulation method based on local mean decomposition and its application in rub-impact fault diagnosis［J］.Measurement Science ＆ Technology，2009，20(2):025704.

［4］ Wang Y X，He Z J，Zi Y Y.A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis［J］.Journal of Vibration and Acoustics-Transactions of the ASME，2010，132(2):021010.

［5］ Huang N E，Wu Z H，Long S R，et al.On instantaneous frequency［J］.Advances in Adaptive Data Analysis，2009，1(2):177－229.

［6］ Olhede S，Walden A T.The Hilbert spectrum via wavelet projections［J］.Proceedings of the Royal Society of London Series a-Mathematical Physical and Engineering Sciences，2004，460:955 －975.

［7］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London A，2002，9(12):283 －300.

［8］ Chu F L，Lu W X.Experimental observation of nonlinear vibrations in a rub-impact rotor system［J］.Journal of Sound and Vibration，2005，283(3 －5):621 －643.

［9］ Hu N Q，Wen X S.The application of Duffing oscillator in characteristic signal detection of early fault［J］.Journal of Sound and Vibration，2003，268(5):917 －931.