星载天线反射面传感器多目标优化部署方案

李文博，王有懿，赵志刚，赵 阳

(哈尔滨工业大学 航天学院，哈尔滨 150001)

随着航天事业的迅猛发展，作为卫星重要有效载荷的星载天线呈指向高精度和大型化的发展趋势［1］。其结构尺寸大、刚度小、阻尼低、模态密集等特点，像安装和制造误差所引起的结构局部化，卫星大角度轨道机动、姿态调整和天线机构的大范围运动耦合作用都会使得反射面形状变化，导致模态参数发生变化，进而造成天线系统指向精度的降低甚至失效［1－3］。而按照标准状态设计的控制器由于模态参数发生变化已不能完成结构振动的主动抑制［4］。因此，进行在轨运行状态下星载天线反射面模态参数辨识及主动振动控制研究具有重要的工程意义。

为获取星载天线反射面的高精度模态参数，亟待解决的关键技术就是传感器数量和位置的优化部署。针对该问题，以往学者在设计优化准则和求解算法两方面做了大量开拓性的工作:有效独立法［5］、遗传算法及其改进算法［6－9］、Guyan 缩聚方法［10］、逐步累积法和消去法［11］等优化部署方法。但大多都基于单一优化准则，而在实际工程应用中设计人员往往要兼顾多种优化准则，而不是片面追求某单一准则在数学上的最优。因此，为解决多目标优化问题，文献［12］采用归一化处理方法将其转化为单目标优化问题，并采用自适应遗传算法对单一权重组合下的优化目标进行求解。但此方法未给出其他权重组合下的最优解集合;文献［13］采用基于小生境技术的Pareto遗传算法进行多准则优化求解，并给出了所有权重组合下的最优解集，但需设置种群小生境半径，人为主观因素影响很大。

综上所述，引入带精英策略的非支配排序遗传算法(NSGA－Ⅱ)，解决以星载天线反射面模态参数在轨辨识为应用背景的传感器多目标优化部署问题。考虑到NSGA－Ⅱ算法仅适合于连续性优化变量，存在收敛速度及多样性保持等方面的不足，对该算法在编码方式和遗传算子设计两方面进行改进。

1 问题的数学描述

多目标优化部署问题的数学模型如下:

其中:X=(x1，x2，…，xn)T为n维决策变量空间;Fi(X)为目标函数，且相互之间是冲突的，即不存在X使得所有子目标函数同时取最小值;gi(x)为约束函数。

通过以上数学模型可知，多目标优化问题的解不同于单目标优化问题:其最优解不是单一解，而是一个最优解集，而该解集中的解无法进一步比较之间的优劣性，称该解集为Pareto最优解集。由此引出以下数学定义［13］:

(1)Pareto最优解:对于可行解x*∈X，当且仅当不存在另一个可行解x∈X使Fi(x)≤Fi(x*)，i=1，2，…，n成立，且至少存在一个i0，i0∈{i=1，2，…，n}，使不等式Fi0(x)≤Fi0(x*)严格成立，则称x*为多目标优化问题的一个Pareto最优解。

(2)Pareto支配关系:对于变量p支配q(p≻q)满足以下两个条件:①Fk(p)≤Fk(q)，k=1，2，…，n;②至少存在一个l∈{i=1，2，…，n}，使Fl(p)≤Fl(q)。

(3)Pareto最优解前沿面:{X*}为给定多目标优化问题的最优解集，其前沿面定义如下式:

(4)Pareto非劣解集(非支配集):解集P中的个体x不被其他任何个体支配，则x为P中的非劣解;P中所有非劣解构成的子集称为非劣解集，其数学描述为:

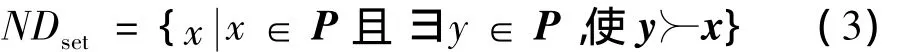
2 优化准则及算法设计

2.1 优化准则设计

为满足星载天线反射面在轨模态参数辨识的应用目的，要求传感器的测量信息既具备较高的信噪比和能量，又有较高的可分辨性。但这两个准则在实际应用中往往是相悖的，在保证测量信息正交性最大时所获得的信号信噪比往往很低，必然对数据采集准确性造成很大影响;而在保证获得高信噪比数据时，又很难保证获得信息的正交性，会造成部分信息冗余而其余部分信息丢失。

理论上结构各阶模态向量是一组正交向量，但由于传感器测量自由度远小于结构模型的自由度并且测量信号受到仪器精度和环境噪声的影响，实际上测得的模态向量不能保证其正交性。因此，在选择测点时有必要使测量的各模态向量保持较大的空间交角。用模态置信度矩阵(MAC)来评价模态空间交角:［8 －9，14］

采用MAC矩阵的非对角元素均方根最小作为目标函数，其数学表达式为:

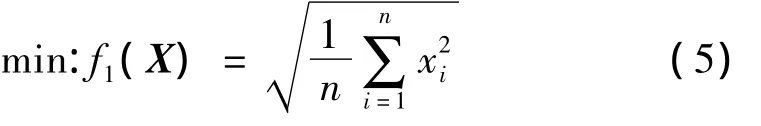
式中，xi表示MAC矩阵的非对角线元素;n表示MAC矩阵的非对角线元素个数。

为保证测量信号具有较高的信噪比和能量，需将传感器部署在具有较大变形能或模态位移的节点上。采用模态振型矩阵的格莱姆矩阵元素和来评价自由度位移的量级，以保证测量信息能量最大［12－13］:

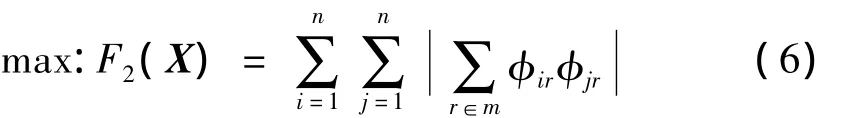
2.2 优化算法设计

(1)NSGA－II算法

针对以往传感器多目标优化问题研究中存在需要过多人为因素参与的情况，引入具有较高计算性能和较少人工经验参与的NSGA－II算法。NSGA－II算法是Deb［15］在Srinivas所提出的NSGA算法基础上，对其存在的缺陷进行改进而得。其具体改进为:① 为克服NSGA运算复杂度高的缺陷，提出基于分级的快速非支配排序法，使其计算复杂度由O(MN3)降低为O(MN2)。其中，M为目标函数个数;N为种群规模;②为克服优秀解丢失的缺陷，引入精英策略自动将上一代的优秀解保留至下一代，无需人为确定共享参数;③为克服样本早熟的缺陷，提出拥挤度和拥挤度比较算子。NSGA－II算法流程如图1所示。

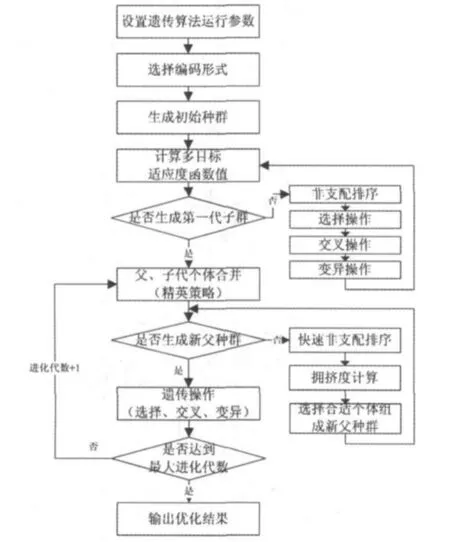
图1 NSGA－II流程图Fig.1 The flowchart of NSGA － II

从图1中看出，NSGA－II的核心为基于拥挤度比较计算的非支配排序方法。其具体操作过程为:首先将父代种群和子代种群合并为一个新的种群;然后对新种群中的个体两两进行比较获取其非劣解集;最后按照拥挤度比较算子以拥挤度距离降序的方式对非劣解集进行排序。

(2)NSGA－II算法改进

虽然NSGA－II在多目标优化领域中得到了广泛应用，但该算法要求优化参数必须是连续性变量，而传感器多目标优化部署问题属于典型的组合优化问题其参数是离散型变量。基于此，对该算法在编码方式和遗传算子设计两方面进行改进，使之可用于离散型变量优化求解。

考虑到星载天线反射面属于典型的薄壁壳体结构，在进行编码方式选择时采取假设条件:① 所有传感器均部署在反射面有限元模型的节点上;② 每个节点只考虑x，y和z三个方向的位移自由度，不考虑x，y和z三个方向的转角自由度。

编码方式采用整数矩阵的形式，矩阵的行数代表可行解群的数量，即种群规模s;列数代表每个可行解的长度，即传感器部署的个数l;每个元素必须是整数，代表所对应传感器部署位置的编号。考虑到程序编写方便，传感器编号顺序与有限元模型x，y和z三个方向的模态振型保持一致。其编码形式如表1所示。

由于NSGA－II所采用的 SBX(Simulated Binary Crossover)交叉算子编码形式为二进制，且全局搜索性能相对较弱。采用具有更好全局搜索能力，并能保持种群多样性的有序交叉算子，其具体形式为:首先确定交叉点的两个位置;然后复制两交叉点之间的元素到新个体;查看交换后的新个体中元素是否有重复，如果没有重复则完成交叉操作;如果有重复，则将交叉点以外的元素按照与交叉点重复元素所对应位置的原个体进行替换，如图 2所示。

图2 有序交叉算子Fig.2 Ordered crossover

表1 传感器部署位置编号Tab.1 The location number of deployed sensors

选择算子采用适合离散型变量的二元锦标赛选择算子，并在计算过程中采用精英保持策略;变异算子采用基本位变异，即随机选取变异点位置，并将该位置参数用随机生成数据代替生成新个体。如果新个体中没有重复参数，则完成变异操作;如果有重复参数，将该变异点参数重新变异再次与其他参数进行比对直到没有重复变量为止。

3 仿真算例

3.1 有限元模型

采用有限元软件MSC.Patran建立如图3所示的星载天线反射面有限元模型。其中，反射面曲线为双曲抛物面，其表达式如式(7)所示;反射面直径6 m，壁厚10 mm;材料密度 ρ=2 800 kg/m3，泊松比r=0.33，杨氏剪切模量G=70 GPa;本模型共有100个壳体单元，101个节点。

式中:f表示双曲抛物面焦距，f=1.5。

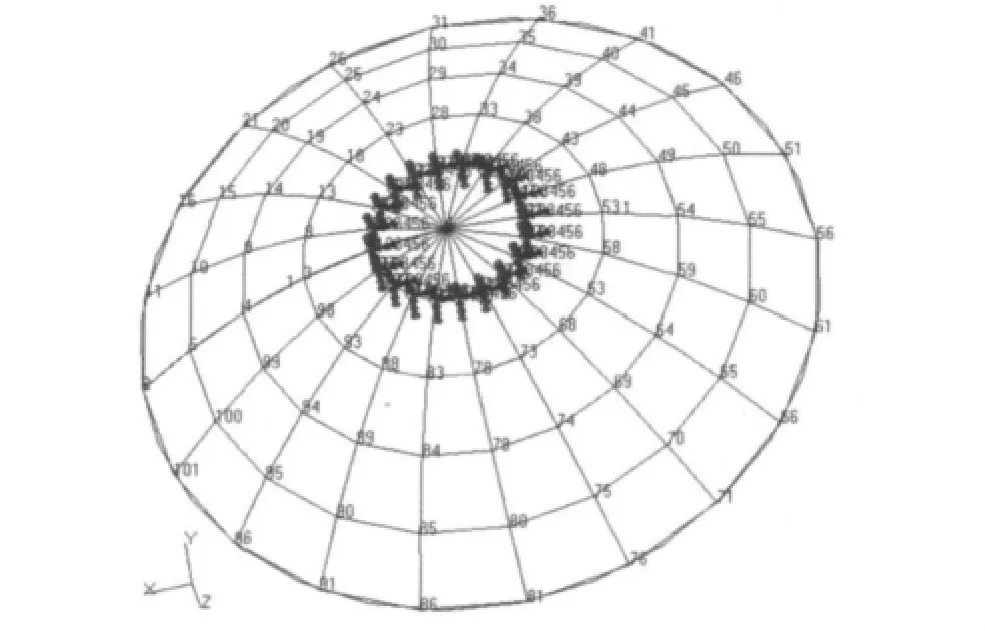
图3 星载天线反射面有限元模型Fig.3 The finite element model of satellite antenna reflector

对图3所示模型进行模态分析，提取其x，y和z方向的模态振型向量，及前8阶模态频率，详见表2。

表2 星载天线反射面有限元模型前8阶模态频率Tab.2 The first eight order modal frequency of finite element model for satellite antenna reflector

3.2 优化方案

表3 四种优化方案的优化准则Tab.3 The fitness function of optimization criterions in four cases

为了对比单目标与多目标优化的计算结果，设计了四种方案完成星载天线反射面传感器部署问题的优化求解，详见表3。其中，方案1、2属于分别基于测量信息正交性最大和能量最大优化准则的单目标优化问题;方案3采用文献［13］归一化方法将方案1和2的多目标优化问题转换成单目标求解;方案4兼顾方案1、2的多目标优化准则。

方案1，2和3均采用遗传算法进行单目标优化问题的求解，其相应参数设置为:种群规模s=200，最大遗传代数G=350，传感器个数l=20;方案4采用改进NSGA－II算法进行多目标优化求解。

3.3 优化结果

图5为方案1－4所得传感器优化部署位置，从中可以看出，方案1所部署传感器覆盖信息全面、分布均匀，但有个别传感器部署在模态位移能量较小(越靠近顶部位置模态位移越小)的节点上;方案2所部署传感器集中在局部振型较大位置，这造成部分测量信息冗余而其余部分信息丢失，不能完全表现出结构本身特征;方案3和4均保证测量信息具有较大正交性和较高能量，使得传感器均部署在振型较大位置，且分布均匀、覆盖信息完整。图6和表4分别表示方案1－4所得优化指标，从中可以看出:方案1的MAC矩阵非对角线元素均方根、最大值和格莱姆矩阵元素和这三项指标在四种优化方案中均最小;方案2中三项指标均最大;而方案3和4居中。

由以上可知:方案3和4是方案1和2的折衷解，既保证测量信息具有较大正交性，又使测量信号可以获取较高的模态位移能量，更加符合实际工程中兼顾多指标的设计要求。

由图4可知，基于归一化方法求解多目标优化问题的方案3所得结果为某单一权重组合下的一个最优解;基于NSGA－II算法的方案4所得结果为一个含有所有权重组合且分布均匀的Pareto最优解集。因此，方案3采用归一化方法求解多目标优化问题所得结果是基于NSGA－II算法的方案4所得解集中的一个特例。从方案4所得Pareto最优解集中提取一个最优解与方案3优化结果进行比较，由表4中可知:方案4的MAC矩阵非对角线元素均方根和最大值均小于方案3，而格莱姆矩阵元素则大于方案3。说明方案4的测量信息正交性和模态位移能量均优于方案3。

图4 方案4所得Pareto最优解集前沿面Fig.4 The Pareto solution frontier in case 4

图5 方案1－4所得传感器部署位置Fig.5 The locations of deployed sensors in case 1，2，3 and 4

图6 方案1－4所得MAC矩阵Fig.6 MAC matrix in case 1，2，3 and 4

表4 方案1－4传感器部署位置和优化指标Tab.4 The locations and evaluation indicators of deployed sensors in case 1，2，3 and 4

综上所述，方案3和4较方案1和2更符合实际工程中天线反射面设计的多指标要求，避免了在数学上片面追求某单一指标最优所存在的缺陷。方案4中所选一个结果的优化指标较方案3的结果均更优，且方案4能给出所有指标权重组合且分布均匀的最优解集。为实际设计中拥有更多的选择空间，并且保证优化结果具有更高的灵活性与适应性。

4 结论

为实现星载天线反射面模态参数在轨高精度辨识，对传感器多目标优化部署问题进行深入研究，具体工作及结论如下:

(1)为实现模态参数在轨辨识的工程应用，设计了观测信息正交性最大和能量最大的双优化准则。

(2)为提高计算性能，避免人为因素参与，引入NSGA－II算法。并对该算法在编码和遗传算子设计两方面进行了改进，使之可用于离散型变量优化求解，扩展了其应用范围，且提高了此算法的全局搜索能力。

(3)对比文中所设计的四种优化方案结果可得:应用改进NSGA－II算法的方案4所得结果，较其他三种方案在性能指标上更优，且该方案更加符合实际工程要求。因此，基于改进NSGA－II算法的优化方案可以很好地解决星载天线反射面传感器多目标优化部署问题。

［1］刘相秋，王 聪，王威远，等.失谐大型天线结构的振动模态局部化研究［J］.宇航学报，2008，29(6):1756－1760.

［2］陈志华，关富玲.星载抛物面天线反射器瞬态热分析［J］.固体力学学报，2008，29(3):272－276.

［3］游斌弟，赵志刚，赵 阳.柔性天线面对漂浮基星载天线扰动分析及抑制［J］.航空学报，2010，31(12):2348－2356.

［4］周 舟，郭铁能，陆秋海.基于在轨辨识的空间柔性结构振动控制［J］.清华大学学报(自然科学版)，2003，43(8):1060－1063.

［5］ Udwadia F E.Methodology for optimal sensor locations for parameteridentification in dynamic systems.American society ofcivilengineers［J］. JournalofEngineering Mechanics，1994，120(2):368 －390.

［6］ Papadimitriou C.Optimal sensor placement methodology for parametric identification of structural systems［J］.Journal of Sound and Vibration，2004，278:923 －947.

［7］Liu W，Gao W C，Sun Y，et al.Optimal sensor placement for spatial lattice structure based on genetic algorithms［J］.Journal of Sound and Vibration，2008，317(1):175－189.

［8］林贤坤，张令弥，郭勤涛，等.协同进化遗传算法在传感器优化配置中的应用［J］.振动与冲击，2009，28(3):190－194.

［9］覃柏英，林贤坤，张令弥，等.基于整数编码遗传算法的传感器优化配置研究［J］.振动与冲击，2011，30(2):252－257.

［10］ Salama M，Rose T，Garba J.Optimal placement of ex-citers and sensors for verification of large dynamical systems［C］.In:Kedward K T ed.Proceedings of SDM conference.AIAA－87 －0782，1987:1024 －1031.

［11］ Clerck J P，Avitabale P.Development of several new tools for modal pretest evaluation［C］.In:Wick A L ed.Proceedings of 14th IMAC conference，1996:1527－1532.

［12］滕 军，朱焰煌.大跨空间钢结构模态参数测试传感器优化布置［J］.工程力学，2011，28(3):150－156.

［13］张连振，黄 侨，王潮海.基于多目标遗传算法的传感器优化布点研究［J］.工程力学，2007，24(4):168－172.

［14］Carne T G，Dohmann C R.A modal test design strategy for modal correlation［C］//Proc 13th International Modal Anal Conf，New York:Union College，Schenectady，1995:927 －933.

［15］ Kalyanmoy D，Amrit P，Sameer A，et al.A fast and elitist multi-objective genetic algorithm:NSGA-II［J］.IEEE Transactions on Evolutionary Computation，2002，6(2):182－197.