基于统计方法的NOPD耗能机理定量分析

崔致远，吴九汇，陈花玲，李涤尘

(西安交通大学 机械工程学院，西安 710049)

非阻塞性微颗粒阻尼(NOPD)技术又称粉体阻尼技术，是一种近些年发展起来的新型阻尼减振技术。它是在结构振动传输路径上，加工一定数量的孔洞，在其中填充适当数量的金属或非金属球形颗粒(颗粒直径范围为0.005～0.5 mm)。随着结构体的振动，粉体颗粒之间不断撞击和摩擦，不但有动量交换，而且能够消耗系统的振动能，达到减振的目的。NOPD具有很多优点，比如:对原系统改动很小、几乎不产生附加质量、显著提高结构的阻尼比、能适用于恶劣环境、减振性能不会随时间降低等，具有广泛的应用前景［1－4］。

针对 NOPD的研究，此前多处于实验分析阶段［5－6］。随着颗粒物质力学的发展，散体单元法(DEM)也已开始应用于NOPD的减振机理研究;基于内时理论的研究也有人涉及。散体单元法(DEM)是一种不连续数值方法模型，其优点在于能够考虑散体中实际颗粒的组成结构，并能根据静力学或动力学原理研究单个颗粒及其总和的性质，适用于模拟离散颗粒组合体在准静态或动态条件下的变形过程［7－9］。文献［10－11］结合NOPD的结构特点，构造了一种球体元模型，认为NOPD的耗能机理分为2种:一种为冲击耗能，另一种为摩擦耗能。影响冲击耗能的主要因素为弹性恢复系数，影响摩擦耗能的主要因素为摩擦系数和法向作用力。文献通过计算机仿真得到NOPD阻尼机理的一般性结论，初步分析了颗粒填充率、颗粒大小等因素对能量耗散的影响。文献［12］也由DEM理论出发，应用牛顿第二定律建立了单个颗粒的运动方程，提出了可由4个弹簧阻尼器和3个摩擦阻尼器代表的颗粒间的接触简化模型，根据赫兹接触理论分析颗粒与颗粒及颗粒与结构之间的接触关系，同时采用“盒式”计算的基本思想，简化了颗粒间接触判别算法，该方法在计算颗粒数较大的问题时，可节省大量计算时间。在上述理论指导下得出的计算机仿真结果显示:系统响应随着质量比的增加而减小，也随着颗粒材料密度的增大而减小，与实验结果具有较好的一致性。但是，当NOPD结构的微颗粒数目较多(超过1万粒)，或者NOPD的结构较为复杂时，该模型的计算效率及精度显得不令人满意。

内蕴时间理论(简称内时理论)由Valanis等［13］提出，并用于描述耗散材料粘塑性过程的理论，内时理论是通过对由内变量表征的材料内部组织结构不可逆变化所满足的热力学约束条件的研究，得到内变量变化所必须满足的规律，从而给出具体材料在具体条件下一条特定的不可逆热力学变量的演变路径。文献［14］应用内时理论分析NOPD的结构响应，确定了材料的内时本构特性，建立起散粒体的增量型内时本构方程，并基于此给出了NOPD结构的有限元动力方程，并用New mark方法对动力方程进行了数值计算，结论认为NOPD阻尼对振幅较大结构的薄弱模态有较好的减振效果，计算结果与实验结果具有较好的一致性。应用上述方法建立的NOPD模型，虽与实验数据有较好的一致性，也具有一定的工程指导意义，但上述研究并未得出NOPD能量耗散的定量规律，颗粒直径、材料密度及颗粒流体积比(颗粒体积/孔洞体积)对能量耗散率的具体影响依然不清楚。

颗粒物质理论中，将颗粒流分为弹性流(弹性准静态颗粒流)和惯性流(惯性碰撞颗粒流)，其研究对象为处于相对简单运动状态的颗粒流。NOPD中颗粒的运动包含了挤压、相对滑动、碰撞等，显然运动形式更为复杂，简单弹性流及惯性流的知识并不能直接应用到NOPD。本文借鉴了湍流的统计处理方法，从研究颗粒之间的能量耗散出发，以NOPD颗粒群整体作为研究对象，建立了颗粒流运动方程及能量方程，得到了NOPD单位质量、单位时间的能量耗散率与颗粒大小及颗粒流体积比等参数的相互关系，所得理论结果与已有实验数据具有良好的一致性。

1 NOPD振动模型的统计处理

本节基于湍流的耗能统计模型，根据颗粒流类流体性质，从颗粒流一般本构关系出发，借鉴局部各向同性湍流的耗能模型，得到了NOPD能量耗散率及能谱密度的表达式。

流体中，当雷诺数超过某临界值时，层流变得不稳定，并开始向湍流过渡。湍流场中，湍动量及湍动能在雷诺应力作用下由均流传递到大涡，再由大涡逐级传递到小涡，最终在小涡中由于粘性作用耗散为热。Kolmogorov［15］由此不仅提出局部各向同性的概念，还提出速度场结构函数D(r)的概念来描述该类湍流速度起伏强度的统计特征，并提出两个著名假设:① 湍流能量传递过程中，能量耗散率ε与运动粘性系数ν是决定能量传递的两个特征量，并通过无因次分析可确定湍流场的特征长度η和特征速度V;② 在惯性副区(r≫η，r为湍流场中任意两点间的距离，η为湍流特征尺寸)，湍流场的纵向速度关联函数与运动粘性系数ν无关。

处于静止或低速运动状态下的颗粒流，各颗粒间相对运动不明显，可认为各点处的速度近似等于一平均速度，表现出与一般流体相似的性质(类流体性)。而NOPD处于工作状态时，其颗粒流在外界振动激励下，各颗粒间发生明显的相对运动，颗粒流内部发生对流［16］，随激振频率的增高，对流现象越明显，不同速度的颗粒之间发生相互挤压、摩擦、碰撞，部分颗粒将不再跟随颗粒流整体一起运动，颗粒的运动状态较运动初期显得混乱无序，当NOPD达到工作平衡状态时，以近似平均速度运动的颗粒流将被具有不同速度的颗粒取代，大量颗粒在振动激励下以各自速度往复运动，呈现出一定的周期性。颗粒对流运动实际上是具有相同运动速度的颗粒组成的“相关层”之间有规则的剪切运动［17］，颗粒流内的动量传递便是由剪切运动导致的速度波动引起［18］。Taguchi［19－20］曾用颗粒湍流模型，用数值模拟方法研究湍流，其研究结果显示:当振动强度超过某个临界值时，颗粒发生流化，出现与完全发展的湍流类似的涡结构，并且，颗粒流中的能谱密度存在与湍流中类似的规律(即kolmogorov用于描述局部各向同性湍流的－5/3定律)。由此，振动颗粒流可看作局部各向同性。所以，本文中将采用湍流局部各向同性模型描述振动颗粒流。

颗粒流动的一般本构关系由文献［23］用连续介质力学中一般方法得到:

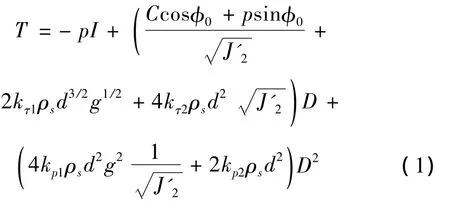
其中，C为颗粒间粘滞力，φ0为颗粒材料静止内摩擦角，p为接触压力，d为颗粒粒径，ρs为颗粒密度，D为变形速度张量，I为张量D的不变量，kτ，kp，为与颗粒体积比ψ、颗粒流发生剪切变形的临界体积比以及颗粒弹性恢复系数有关的应力系数，J2’=1/2trD2，kτ1=kp1tanφ1，kτ2=kp2tanφ2，φ1，φ2分别定义为滑动摩擦角和碰撞摩擦角。NOPD颗粒间存在法向粘滞力及切向摩擦力，但法向粘滞力的影响较小，一般不予考虑(C=0)，由于颗粒对流实际上是有规则的简单剪切运动，即为简单剪切流V1=U(y)，V2=V3=0，本构方程可简化为:

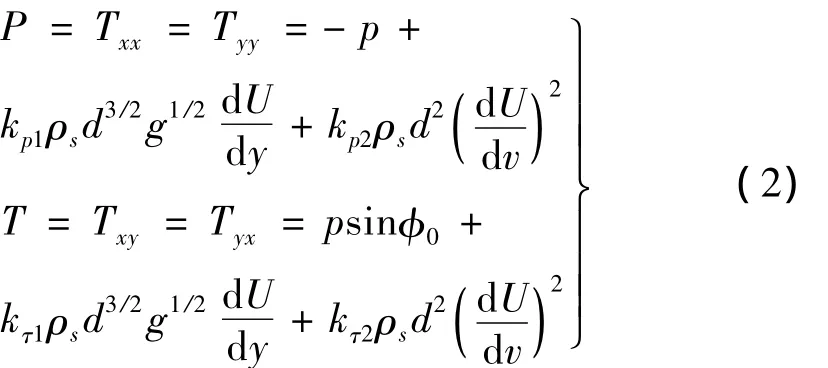
其中速度梯度(dU/dy)零次项由颗粒之间静态支撑作用引起;速度梯度线性项由颗粒之间的相对滑动和挤压作用引起，该项可被看作耗散项，颗粒间通过相互挤压、摩擦耗散外界能量，因此与能量耗散有关的参数为速度梯度线性项系数kp1ρsd3/2g1/2与kτ1ρsd3/2g1/2，其中kp1，kτ1为无因次量;速度梯度二次项是由颗粒间的碰撞和扩散作用引起，该项为对流扩散项，其作用是使能量在颗粒间重新分配，并不改变能量总和。

令ν=d3/2g1/2，并引入表征颗粒流特征参数:特征速度u与特征尺度η，通过无因次分析得到由ε与ν表示的特征参数表达式:

当两点速度与其连线同向时，用Bdd(r)表示该两点的速度关联函数，称为纵向关联函数。依据相似假设，在局部各向同性区域内，Bdd(r)与等效运动粘性系数 ν 无关［15，24］，得到:

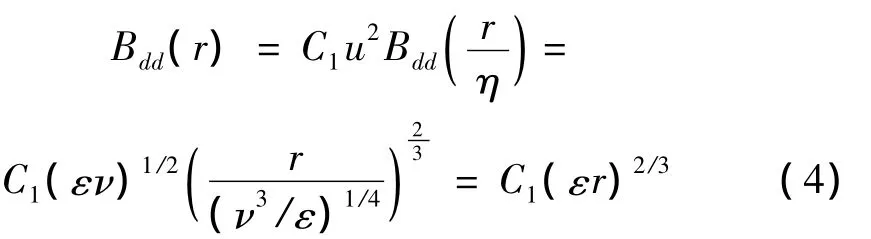
其中，βdd为(r/η)的普适函数，C1为常数，由实验确定。

能谱密度也有类似定律，在振动强度较高的情况下有:

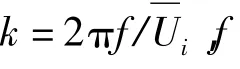
由式(4)、式(5)可发现，NOPD能量耗散率及能谱密度的表达式形式与湍流理论中Kolmogorov假设的相关结论一致，将通过实验数据分析验证该结论。

2 NOPD颗粒流的能量关系

从N－S方程出发，结合颗粒流一般本构关系，建立适应颗粒流动量守恒方程(广义N－S方程)及能量守恒方程，分析NOPD工作状态下的能量转移、分布及耗散等状态间的关系。

确定偏应力时，颗粒流一般本构关系中的速度梯度零次项是不重要的［25］，由无粘条件，可将本构关系式(1)写为:

将式(6)代入N－S方程，令:

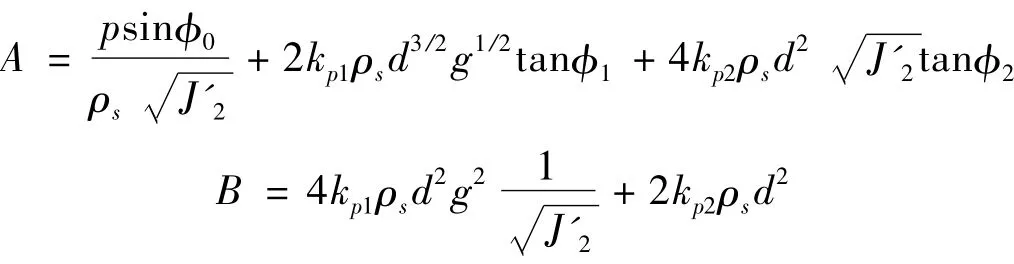
可得到不可压缩条件下颗粒流的动量守恒方程(广义N－S方程)和连续方程:

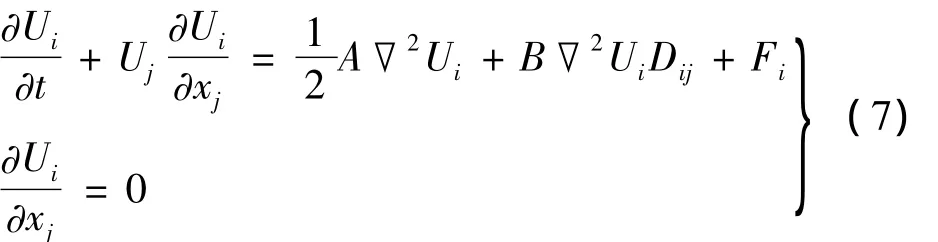
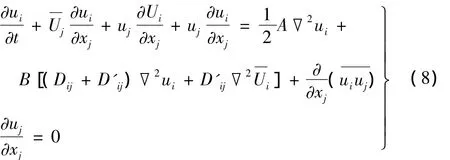
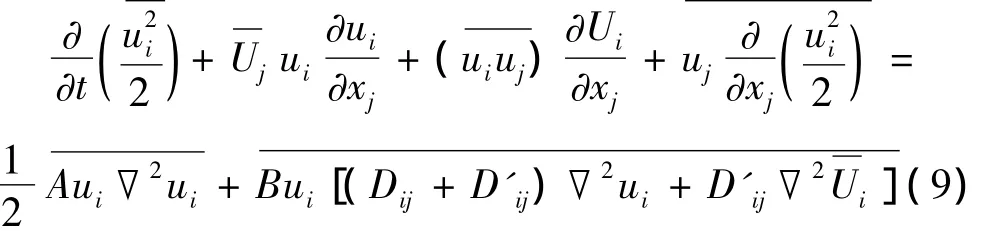
考虑连续方程，整理(9)式右边第一项，得:

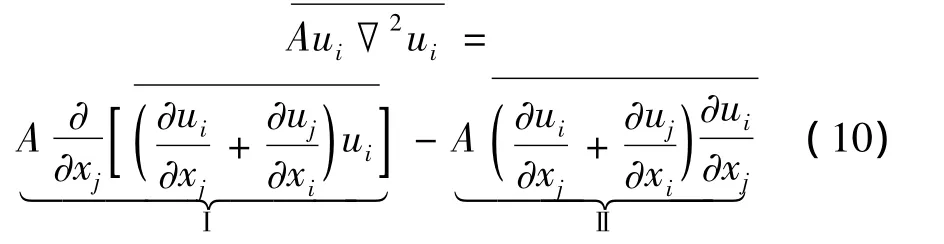
其中Ⅰ项为脉动运动中粘性切力做的功，即脉动速度产生的动能平均输送项，表示脉动对平均流的影响;Ⅱ项为脉动运动中的能量耗损项，用ε表示。

3 NOPD颗粒流的能量关系数据分析

根据以上文中得到的NOPD能量耗散率表达式，结合已有实验数据，画出能量耗散率ε随颗粒流体积比及颗粒大小等因素的变化曲线，将所得能量耗散率的变化规律与已有的相关结果进行对比。处于湍动平衡状态的颗粒流，虽然整体上并不处于简单剪切流状态，但可认为其中某小部分颗粒群处于简单剪切运动状态。由无粘条件及简单剪切流假设，公式(10)中Ⅱ项(能量耗散率ε)可表示如下:

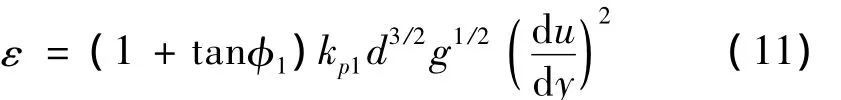
图1 三种不同颗粒直径(d)的颗粒流在du/dy=100 s－1时，能量耗散率 ε随颗粒体积比ψv的变化曲线Fig.1 Mean energy dissipation(ε)curve(log － log)for different values of volume ratio(ψv)，when d=1.8mm，d=1.1mm，d=0.5mm;du/dy=100 s－1.

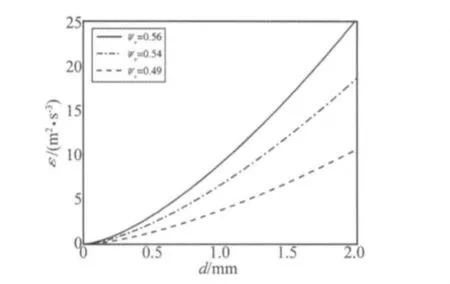
图2 三种不同体积比(ψv)颗粒流在du/dy=100 s－1时，能量耗散率ε随颗粒直径d的变化曲线Fig.2 Mean energy dissipation(ε)curve for different values of particle diameter(d)，when ψv=0.56，ψv=0.54，ψv=0.49，du/dy=100 s－1.

由图1可见，在相同颗粒大小、相同速度梯度情况下，颗粒流体积比越高颗粒间发生的碰撞及摩擦越多，从而使NOPD的能量耗散率随体积比的增加而平滑上涨;当颗粒流体积比超过60%时，NOPD的能量耗散率迅速增加，并趋于其最大值。在研究颗粒流体积比对NOPD阻尼效果影响的文献中，也有相同的变化规律，即振动的耗散时间在颗粒流体积比超过60%时急剧减少，并趋于其最小值［27］。图 2为在相同体积比时，NOPD的能量耗散率随颗粒尺寸的增大而增加，体积比较高时，颗粒尺寸的增加会导致更加显著的能量耗散率的变化。此前的研究结果也证实了该变化规律的正确性［6］。上述对比证明了利用湍流耗能模型分析NOPD耗能问题的可行性和正确性。

图3所示，能谱密度E与频率f的变化成反比。当振动强度较高时，颗粒间才会发生对流现象，此时颗粒相关层中的剪切运动比较低振动强度时更剧烈，从而导致更多的能量耗散。该现象与湍流由惯性区向耗能区的转变过程极为相似。

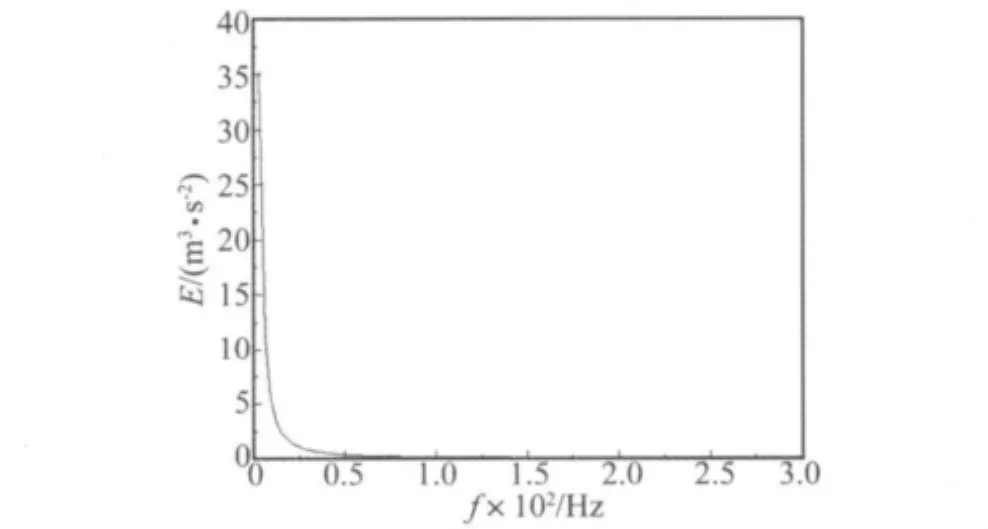
图3 ψv=0.56，d=1.1 mm 的干颗粒流，能谱密度E随频率f的变化曲线Fig.3 Energy spectral density(E)curve for different values of frequency(f)，when d=1.1mm，ψv=0.56.

4 结论

本文提出了一个分析NOPD能量耗散机理的定量模型，并得到了满意的理论结果，结论表明:颗粒直径越大、颗粒流体积比越高，NOPD的能量耗散率就越高;相同能量耗散率情况下，能谱密度随着波数的增加而降低。能量耗散率的分析结果与参考文献中的实验数据有较好的一致性，说明湍流耗能模型对NOPD的耗能过程具有适用性。

该理论模型能更好的适应大量的颗粒及复杂结构条件下NOPD的耗能分析，对工程应用有一定的指导作用。该模型的建立，为更精确地分析NOPD耗能机理以及更好地指导工程应用开辟了一条新的思路。

［1］Xu Z W，Wang M Y，Chen T N.A particle damper for vibration and noise reduction［J］.Journal of Sound and Vibration，2004，207(4 －5):1033 －1040.

［2］Panossian H V.Structural damping enhancement via nonobstructive particle damping technique［J］. Journalof Vibration and Acoustics，1992，114:101 －105.

［3］Panossian H V，Kovac B，Rackl R.Composite honeycomb treatment via non-obstructive particle damping(NOPD)［R］.Proceedings ofthe45thAIAA/ASME/ASCE/AHS/ASC Structures;Structural Dynamics ＆ Materials Conference，2004，1689.

［4］Panossian H V.Ehrgott R.Non-obstructive particle damping(NOPD)treatment optimization for composite honeycomb panels［R］.Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures:Structural Dynamics and Materials Conference，2007，2047.

［5］Xu Z W，Wang M Y，Chen T N.Particle damping for passive vibration suppression:numericalmodeling and experimentalinvestigation［J］. JournalofSound and Vibration，2005，279:1097 －1120.

［6］Xu Z W，Wang M Y，Chen T N.An experimental study of particle damping for beams and plates［J］.Journal of Vibration and Acoustics，2004，126:141 －148.

［7］Mao K M，Wang M Y，Xu Z W，et al.DEM simulation of particle damping［J］.Powder Technology，2004，142:154－165.

［8］Wong C X，Daniel M C，Rongong J A.Energy dissipation prediction of particle dampers［J］.Journal of Sound and Vibration，2009，319(1 －2):91 －118.

［9］Saeki M.Impact damping with granular materials in a horizontally vibrating system［J］.Journal of Sound and Vibration，2002，251(1):153－161.

［10］MaoK ，Wang M，Ding H，et al.Simulation and characterization of particle damping in transient vibrations［J］.Journal of Vibration and Acoustics，2004，126(2):202－211.

［11］Chen T N，Mao K ，Huang X Q，et al.Dissipation mechanism of non-obstructive particle damping using discrete element method［J］.In:Proceedings of SPIE International Symposium on Smart Structures and Materials.Damping and Isolation，2001，4331:294 －301.

［12］Hu L，Huang Q，Liu Z.A non-obstructive particle damping model of DEM［J］.International Journal of Mechanics and Materials Design，2008，4:45 －51.

［13］ Valanis K C，Fan J.A numerical algorithm for endochronic plasticity and comparison with experiment［J］.Computers ＆Structures，1984，19(5):717 －724.

［14］王 炜，黄协清，陈天宁，等.内蕴时间理论用于NOPD结构相应计算的研究［J］.力学学报，2003，35(2):246－252.

［15］ Kolmogorov A N.The local structure of turbulence in incompressible viscous fluid for very large reynolds numbers［J］.Proceedings:Mathematical and Physical Sciences，Turbulence and Stochastic Process:Kolmogorov＇s Ideas 50 Years On，1991，434(1890):9 －13.

［16］ Eshuis P，Meer D V D，Alam M，et al.Onset of convection in strongly shaken granular matter［J］.Physical Review Letters，2010，104(3):038001.

［17］ McNamara S，Luding S.Energy flows in vibrated granular media［J］.Physical Review E，1998，58:813 －822.

［18］Gioia G，Ott-Monsivais E，Hill K M.Fluctuating velocity and momentum transfer in dense granular flows［J］.Physical Review Letters，2006，96(13):138001.

［19］ Taguchi Y H.Turbulent flow in vibrated bed of powder:new target to investigate turbulent flow［J］.Fractals，1993，1(4):1080－1085.

［20］ Taguchi Y H.K-5/3 Power spectrum in Powder-turbulent flow in a vibrated bed:numerical results［J］.Europhysics Letters，1993，24(3):203 －209.

［21］ Taguchi Y H.Powder turbulence:direct onset of turbulent flow［J］.Journal de Physique II 2，1992:2103 －2114.

［22］ Losert W，Bocquet L，Lubensky T C，et al.Particle dynamics in sheared granular matter［J］.Physical Review Letters，2000，85:1428 －1431.

［23］王光谦，熊 刚，方红卫.颗粒流动的一般本构关系［J］.中国科学E辑:技术科学，1998，28(3):282－288.

［24］Kolmogorov A N.Dissipation of energy in the locally isotropic turbulence［J］.Proceedings:Mathematical and Physical Sciences，Turbulence and Stochastic Process:Kolmogorov＇s Ideas 50 Years On，1991，434(1890):15 －17.

［25］韩式方.非牛顿流体连续介质力学［M］.成都:四川科学技术出版社，1988.

［26］ 陆厚根.粉体工程导论［M］.上海:同济大学出版社，1993.

［27］Wakasawa Y，Hashimoto M，Marui E.The damping capacity improvement of machine tool structures by balls packing［J］.International Journal of Machine Tools＆ Manufacture，2004，44(14):1527－1536.