基于约束独立成分分析的滚动轴承故障诊断

王志阳，陈 进，肖文斌，周 宇

(上海交通大学 机械系统与振动国家重点实验室，上海 200240)

独立成分分析(ICA)是一种从多维统计数据中寻找隐含变量或成分的方法。区别于其它方法的本质特征是这些成分既是统计独立的又是非高斯的［1］。独立成分分析(ICA)已广泛应用于通信工程［1-2］、语音处理［2-4］、生物工程［5-6］等许多领域，但在机械故障诊断中的应用仍然面临许多困难。目前的发展趋势表明，ICA只有与被应用对象相结合，才会有比较理想的效果。因为ICA仅利用数据统计的独立性进行分离，虽然适用性广泛，但其缺点也较明显。即ICA所利用的信息太过单一，是ICA具有幅值不定性和顺序不定性的根本原因。而实际工程中所测得的数据除具有统计独立性属性外，还具有诸如时间结构等其它工程属性。独立成分分析与机械故障诊断的关系也是如此。只有与机械故障诊断对象的先验信息相结合，才能提高故障诊断的准确性和成功率。另外，ICA的具体的应用中，当被应用的对象确定后，其许多信息是已知的、可利用的。而约束独立成分分析方法可以满足这些要求。

如何从大量的数据中提取有用信息是机械故障诊断的显著特点。约束独立成分分析(cICA)将被研究对象的先验信息融入ICA算法中，使算法在收敛的时候仅仅收敛于感兴趣的故障信号，不仅可以提高故障诊断的针对性，且大大减少了计算量。因此约束独立成分分析方法在机械故障诊断领域有巨大的应用前景。

迄今为止，约束独立成分分析方法在机械故障诊断中的应用还相对较少。本文论述约束独立成分分析方法的一般原理和方法，分析约束独立成分分析方法在机械故障诊断中参考信号产生的原则和方法，并通过实验验证该方法在滚动轴承故障诊断中的适用性和有效性。

1 方法

1.1 独立成分分析(ICA)

约束独立成分分析(cICA)由独立成分分析(ICA)发展而来。此处介绍ICA，再引出cICA的原理与方法。

基本的ICA模型为:假设k个可观测的时间序列x(t)=［x1(t)，x2(t)，…，xk(t)］由l个满足独立性的未知非高斯性源信号s(t)=［s1(t)，s2(t)，…，sl(t)］线性混合而成(l个信号源中至多有一个高斯性信号)，即:

则ICA方法在混合矩阵A和源信号向量s(t)均未知的条件下，求一个矩阵W，使得W对混合信号x(t)的线性变换:

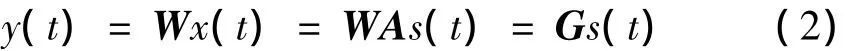
对源信号s(t)或其某些分量的一个可靠估计。式中W称为分离矩阵，C称为全局矩阵或者混合-分离矩阵。

由中心极限定理知，独立随机变量之和的分布较任何一个原随机变量更接近于高斯分布。因此，非高斯性是ICA估计的基础。由信息理论，在所有方差相同的随机变量中，高斯变量具有最大的熵，即，高斯变量是最随机的。因此可用负熵度量非高斯性。负熵定义为:

负熵总是非负的，当且仅当y具有高斯分布时，负熵为零。对于可逆的线性变换，负熵也为不变量。最大化(3)式会产生一个独立成分，即著名的One-Unit ICA算法［7］。采用负熵度量非高斯性所遇到的问题使其计算非常困难，按定义估计负熵需估计概率密度函数，常用某些近似方法［8］。此种方法是将高阶矩阵近似地加以广义化，即:

其中:ρ为正常数，v为零均值单位方差的高斯变量，G(·)为非二次函数。已经证明下列形式是有用的:

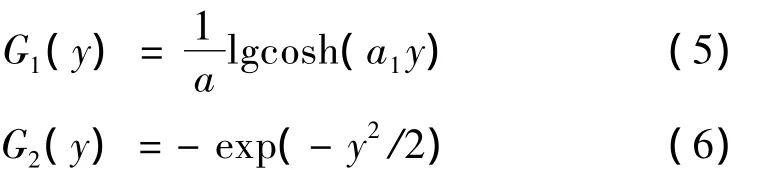
式中:1≤a1≤2，常取作1。然后利用下面的定点迭代算法:

式中g是G的导数。α可用近似牛顿迭代方法搜索。

1.2 约束独立成分分析(cICA)

One-Unit ICA方法理论上收敛于负熵的最大值。因此提取的独立成分是混合信号中非高斯性最大的那个。如果想提取某个特定的独立成分，除非该成分恰好就是非高斯性最大的那个，否则one-unit ICA方法就会失效。如果在One-Unit ICA的收敛算法中加上一个约束条件，当该约束条件包含了感兴趣信号的特征时，算法就会收敛于需要的独立成分［9］。假设该约束条件可以表示成参考信号r(t)。定义待提取的独立成分y和参考信号r(t)的距离函数为 ε(y，r)。ε(y，r)可用均方误差ε(y，r)=E{(y-r)2}度量，也可用相关函数ε(y，r)=-E{yr}度量。则有以下不等式:

其中:w*是欲抽取的独立成分对应的最优解混向量，wi(i=1，2，…，l-1)是其它独立成分对应的解混向量。则下述的约束函数有且只有在y=w*Tx时为真:

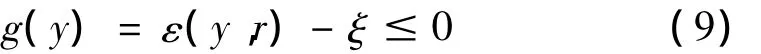
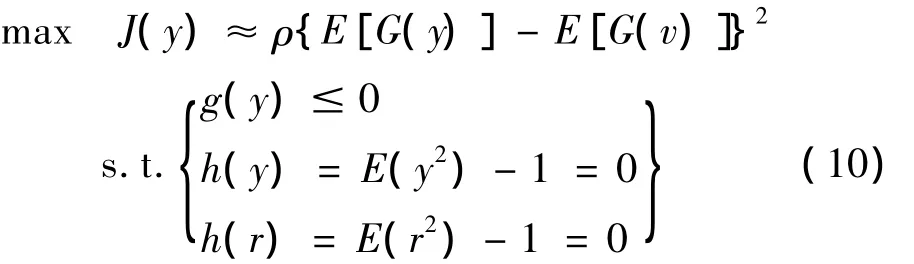
式中:J(y)为式(4)中描述的one-unit对照函数;g(y)是约束函数;h(y)和h(r)是分别约束输出的独立成分y和参考信号具有单位方差。式(10)实际上是一个约束优化问题，可通过拉格朗日乘数法求解。

1.3 参考信号的建立

约束独立成分分析方法中的参考信号应该满足两个要求:① 反映待提取信号的特征。该要求为独立成分分析方法中参考信号存在的根本原因。即，参考信号要包含应用对象的先验信息。此处仅需要参考信号反映待提取信号的特征，非待提取信号本身。该特性对建立参考信号具有重要的指导意义。② 参考信号是非高斯性信号或者可以转换为非高斯性信号。约束独立成分算法以独立成分分析算法为基础。而独立成分分析以数据的非高斯为基础，对照函数非高斯性(负熵)最大化求解。约束条件(参考信号)的加入只是改变并且能够改变算法的收敛方向。因此，约束条件要能够转化为以非高斯性(负熵)为因子(自变量)的等式或不等式影响算法的收敛。

在机械故障诊断领域，有些先验知识为已知的，如齿轮的啮合频率，滚动轴承的特征频率等。这些都可以作为约束独立成分分析(cICA)的约束条件。约束独立成分分析中的参考信号不必和感兴趣的信号完全相同，也没有必要完全相同，否则cICA方法就失去了意义。在机械故障诊断中，故障往往表现为一系列有规律的冲击。比如，工况稳定时滚动轴承的故障表现为频率恒定的冲击序列。因此可以把冲击的周期作为约束条件，使cICA算法收敛于故障信号，即将感兴趣信号对应的参考信号处置为单位方波而其它的区域置为零。

可以看出，这种参考信号建立方法由于其包含了被提取信号的周期，满足参考信号建立的第一个要求。又因为它是一列方波序列。该参考信号为非高斯性信号，满足约束独立成分分析对参考信号要求的第二个条件。这种建立参考信号的方法称为脉冲法。此方法本质上是一种时域形状特征约束，已经在医学工程特别是脑电图(ECG)、脑磁图(EEG)中有比较成功的应用［11-13］。James等［14］已经指出:参考信号的形状应尽可能与被抽取信号一致，或者每个方波的初相位应该与被抽取信号的初相位一致。例如，在机械故障诊断中，如果要设计一个方波脉冲序列作参考信号，欲抽取一个50 Hz的旋转频率，只需要在用相关函数度量的情况下，每(1/50)s/(1/2 000)s=40个抽样点要有一个波峰相关(这里抽样频率假设为2 000 Hz)。至于cICA算法中的阈值参数选择问题，已有比较详尽的讨论［11-15］，此处不再赘述。

2 计算机仿真及分析

计算机仿真的目的是用cICA方法从合成的混合信号中抽取出故障信号。图1是源信号的时域波形。源信号s1是一个锯齿波。源信号s2是一内圈故障的滚动轴承信号，来自Randall［16］的故障轴承模型。它综合考虑了滚动轴承的结构形状、公差、幅调、滑移和表面破坏的因素。该模型在文献［16-18］中已成功应用。s3是一个高斯白噪声信号。随机产生一个混合矩阵A，上述三个信号按式(1)混合。图2为可观测的3个混合信号的时域波形。

实际工作中滚动轴承型号与转速是已知的，因此其特征频率可通过公式计算或查表法获得［19］。现产生一方波序列，使其周期等于模拟故障轴承的特征频率，并以此为参考信号。用均方误差作为参考信号和提取信号的相似性测度。图3(a)为一个周期等于滚动轴承内圈通过周期的方波序列，并以此为参考信号，图3(b)为对应的提取信号y的时域波形。

为更清楚地分析已提取出的信号，对抽取出的信号做包络谱分析。图4为图3(b)中信号y的包络频谱图，从图4看出，在118.3 Hz处的两边等间距(16.67 Hz)地分布着100 Hz与135 Hz。这是内圈故障频率被转频调制的典型特征。因此，利用cICA方法正确地提取出了故障信号。

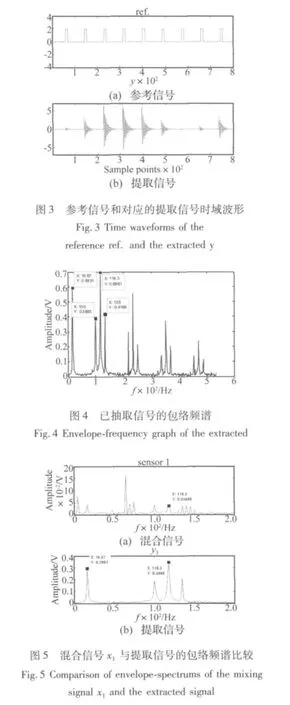
图5是混合信号x1(相当于一路传感器信号，这里假设为传感器1)和提取信号的包络频谱比较图。从图5中看出，提取信号的包络频谱仅包含了故障信号的信息，而传感器1的包络频谱图中故障信号的频谱不明显，并且包含了其它一些频率成分。这表明，约束独立成分分析由于仅仅提取了感兴趣的故障信号，因此它的包络频谱比传感器信号的包络频谱更加“干净”和清楚。

如果用不正确的参考信号作为约束条件。例如使参考信号的频率f=0.3fp(fp是滚动轴承的内圈通过频率)。图6是利用cICA方法的抽取结果。结果显示:此时没有抽取出正确的故障信号。反复的实验表明，只有正确的参考信号才能提取出感兴趣的故障信号，不正确的参考信号无法提取出故障信号。

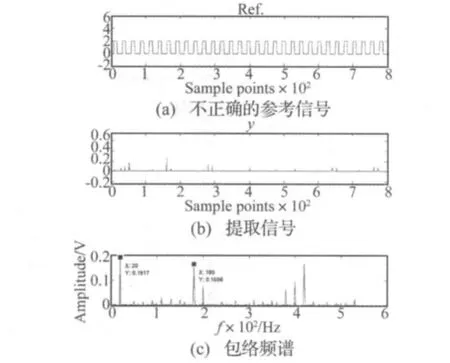
图6 不正确的参考信号和提取信号y的时域波形以及y的包络频谱Fig.6 Time waveforms of the improper reference signal and the extracted signal y，and the corresponding envelope-spectrum graph of the extracted signal y

3 滚动轴承实验及分析

实验数据来自上海交通大学机械系统与振动国家重点实验室。滚动轴承振动测试台和传感器布置如图7所示。该试验台由交流电机驱动，通过联轴器带动转子运转。在测试过程中，滚动轴承的外圈固定在实验台架上，内圈随工作轴同步转动。试验轴承型号为GB6203，内圈用电火花加工方法加工一弧长×长×宽=0.5×0.5×4(单位:mm)的故障。轴承试件如图8所示。工作轴的转速为720 r/min，经查表计算，轴承的内圈特征频率为59.4 Hz。四个传声器的位置如图8所示。信号采集系统用丹麦 B.K公司的 PULSE 6530C，采样频率为66 kHz。

四个传声器测得的声信号为可观测的混合信号。假设在故障诊断中希望从传感器信号中判断滚动轴承是否发生故障。为使用约束独立成分分析方法，与前面仿真相同，一个频率等于滚动轴承内圈通过频率(fip=59.4 Hz)的方波序列作为参考信号，算法的输出结果示于图9中。从抽取信号y的包络频谱可以看出，内圈故障频率(60.01 Hz)被转频(12.06 Hz)所调制。这表明，故障信号被正确地提取出来了。

如果约束条件使用了不正确的参考信号，例如，使参考信号的周期等于滚动轴承内圈故障周期的0.15倍。则可得cICA算法的输出如图10所示。从图10的包络频谱图中看出，此时轴承的内圈故障信号并没有被提取出来。这表明，不正确的参考信号无法提取出正确的故障信号。这是因为约束条件(参考信号)中没有包含感兴趣信号的特征所致。

4 结论

本文研究了约束独立成分分析方法及其在滚动轴承故障诊断中的应用。综上所述，结论如下:

(1)约束独立成分分析中的参考信号只需要反映被提取信号的特征即可，不必要与被提取信号完全相同。

(2)只有正确的参考信号(反映故障信号的特征)才能提取出需要的故障信号;反之则不能。

(3)仿真表明，高斯性噪音信号在约束独立成分分析中不影响故障信号的提取。

(4)通过约束独立成分分析方法提取出的信号包络频谱比传感器信号的包络频谱更加“干净”和清楚。

［1］ Seungjin C，Andrzej C，Hyung M P，et al.Blind source separation and independent component analysis:a review［J］.Neural Information Processing-Letters and Reviews，2005，6(1):1-57.

［2］Puntonet C G，Lang E W.Blind source separation and independent component analysis［J］.Neurocomputing，2006，69(13-15):1413.

［3］ Hyvärinen A，Hyvarinen.Independent component analysis:algorithms and applications［J］.Neural computation，2001，13(7):1527.

［4］ Oja E，Karhunen J，Valpola H，et al.Independent component analysis and blind source separation［J］.Signal Processing，2007，87(8):1817-1818.

［5］Barros A K，Cichocki A.Extraction of specific signals with temporal structure［J］.Neural Computation，2001，13(9):1995-2003.

［6］ James C J，Gibson O J.Temporally constrained ICA:an application to artifact rejection in electromagnetic brain signal analysis［J］.IEEE Transactions on Biomedical Engineering，2003，50(9):1108-1116.

［7］ Hyvärinen A.One-unit contrast functions for independent component analysis:a statisticalanalysis［J］. Neural Networks for Signal Processing，1997，7:388-397.

［8］ Hyvärinen A.Fast and robust fixed-point algorithms for Independent component analysis［J］.IEEE Transactions on Neural Networks，1999，10(3):626-634.

［9］Lu W，Rajapakse J C. ICA with reference［J］.Neurocomputing，2006，69(16-18):2244-2257.

［10］ Li C，Liao G.A reference-based blind source extraction algorithm［J］.Neural Computing ＆ Applications，2010，19(2):299-303.

［11］ Wei L，RajapakseJC. Approach and applicationsof constrained ICA［J］.IEEE Transactions on Neural Networks，2005，16(1):203-212.

［12］ Welling M.A constrained EM algorithm for independent componentanalysis［J］. Neuralcomputation， 2001，13(3):677.

［13］ Rasheed T.Constrained blind source separation of human brain signals［J］//Department of Computer Engineering.Kyung Hee University:Korea，2010:68-81.

［14］ James J C.Temporally constrained ICA:an application to artifact rejection in electromagnetic brain signal analysis［J］.IEEE Transactions on Biomedical Engineering，2003，50(9):1108-1116.

［15］ Zhang Z L.Morphologically constrained ICA for extracting weak temporally correlated signals［J］.Neurocomputing，2008，71(7-9):1669-1679.

［16］ Randall R B，Antoni J，Chobsaard S.The relationship between special correlation and envelope analysis in the diagnostics of bearing faults and other cyclostationary machine signals［J］.Mechanical Systems and Signal Processing，2001，15(5):945-962.

［17］ Antoni J，Randall R B.Differential diagnosis of gear and bearing faults［J］. American Society ofMechanical Engineers，2002，124(2):165-171.

［18］ Pan Y N，Chen J，Li X L.Spectral entropy:a complementary index for rolling element bearing performance degradation assessment［R］//Mechanical Engineering Science，Dalian P.R.C，2009.

［19］陈 进，机械设备振动监测与故障诊断［M］.上海:上海交通大学出版社，1999.