基于通用旋转组合设计的热板参数分析
王靖震 魏 猛 刘伟军 胡延兵
1.中国科学院沈阳自动化研究所,沈阳,110016 2.中国科学院研究生院,北京,100049 3.沈阳芯源微电子设备有限公司,沈阳,110168
0 引言
在制造大规模集成电路时,人们通过光刻工艺把密集的电子线路刻到晶圆上。在这一工艺过程中,通过热板来对晶圆进行烘焙处理。热板表面的温度均匀性是一个关键的技术指标,在前烘、后烘工序中热板表面的温度均匀性尤为重要[1]。由于在工艺过程中光刻胶在烘焙时所受的张力以及光刻胶中的化学物质对温度高度敏感,热板表面的温度均匀性将会对刻画到晶圆上的电子线路宽度产生很大的影响[2],所以加热时表面温度均匀一致的热板是保证大规模集成电路制造中光刻工艺质量的必要条件。同时随着集成电路集成度的加大和线宽的日益缩小,热板烘焙技术也需要不断发展来进一步提高热板表面的温度均匀性,以适应具有更加密集电子线路晶圆的烘焙要求[2-5]。
最新的热板烘焙技术包括采用电热元器件单元点阵排布的方式对热板进行分区控制[6-7],以及采用热气流通过腔体的表面来加热的方式[8],这些技术都取得了很好的效果。但是相对于传统的热丝加热电热板来说,上述加热方式的制造工艺和控制过程过于复杂和昂贵,并且在工业生产中的稳定性还有待验证。国内对热板技术的研究主要是针对传统的热丝加热电热板技术,采用有限元仿真模拟的方法,对固定数量热丝的排布进行优化[9-10],但是对影响热板表面温度均匀性的其他因素还需要进行进一步的探讨。
通常设计一个具有高度表面温度均匀性的热板,意味着要进行多次实际的物理试验,周期长、成本高。国内学者对于在集成电路制造业中应用的热板的研究较少。本文以某热板设计为例,在热板设计参数选择问题上,利用通用旋转组合设计的方法,对试验先进行规划设计,大幅减少了试验的次数。应用ANSYS仿真模拟软件,仿真模拟不同设计参数条件下的热板表面温度场均匀性情况,然后对试验数据采用SPSS统计软件进行回归分析。建立了热板设计参数与热板表面温度场均匀性之间关系的数学模型,并以此数学模型来指导热板设计参数的选择。
1 热板单元结构与温度场仿真
热板单元几何模型如图1所示,热板分为上下对称的两部分,热丝嵌入上下两部分中间。由于温度场的近似对称关系,只分析热板上半部分温度场即可。图2为热板的热丝排布图,本文中热板采用等螺距螺旋线式热丝均匀排布。

图1 热板单元结构示意图

图2 热丝排布图
根据热学原理的初步分析,影响热板表面温度场均匀性的设计参数主要有:热板上半部分厚度X1;热板热丝间距离X2;热板周围的空气对流换热系数X3,X3的值反映热板周围环境对热板表面温度均匀性的作用。
本文采用ANSYS软件作为热板温度场分析研究的仿真模拟工具。应用有限元仿真模拟技术对热板表面温度场均匀性进行仿真,可以比较直观地了解热板设计参数对热板表面温度场均匀性的影响情况,并且周期短,成本低。图3为热板温度场均匀性仿真模拟图,显示了当烘焙温度为200℃时热板温度场均匀性的情况。
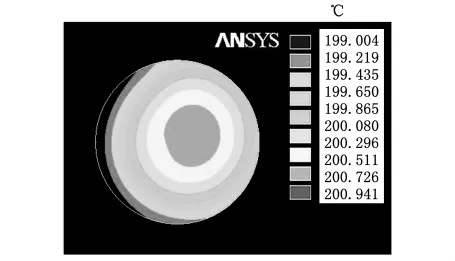
图3 热板表面温度场模拟
仿真模拟的同时,在软件中构造变量T代表仿真结果的温度均匀性数据。数值上T为热板表面烘焙区域内的温度最大差值,用以表示温度均匀性的好坏,可见T越小越好。
2 通用旋转组合设计
试验设计是研究如何科学地安排试验方案以便对试验数据进行有效统计分析即回归分析的数学理论与方法。对于影响热板表面温度场的三个可能的因素来说,它们有可能单独起作用,也可能相互制约。如果要全面地进行试验,试验数量会非常多。通用旋转组合设计是一种研究多因素多水平的试验设计方法,相对于正交试验设计方法,它一方面基本保留了回归正交设计的优点,即试验次数少,计算简便,部分地清除了回归系数间的相关性,即牺牲部分的正交性而获得旋转性。另一方面,通用旋转组合设计能使回归预测值的方差成为在以球心为原点的球内的一个常数,有助于克服回归正交设计中回归预测值的方差依赖于试验点在因子空间中位置的缺点[11]。通用旋转组合设计因其一致精度和需要试验次数较少等优点而广泛应用于科学试验中。由于在实际工程设计中需要对不同的设计参数组合进行比较,如采用通用旋转组合设计,由回归分析模型得出的不同设计参数结果数据精度一致或者说结果数据方差相同,可以使以后的参数选择更为方便合理。
首先应用三因素二次通用旋转组合试验设计方法,按通用旋转组合设计表格求得温度均匀性变量T在相应自变量X1、X2、X3取不同值情况下的仿真试验数据。然后对所得试验数据用三元二次回归分析的方法,建立它们之间的数学模型。
经过通用旋转组合试验设计后,回归分析得到的三因素二次模型如下:式中,β0、βj、βkj、βjj分别为零次、一次、交互和二次项的系数;Xj为各因素的水平值,用X1j和X2j来表示Xj的下限和上限,分别称为因素的下水平、上水平。
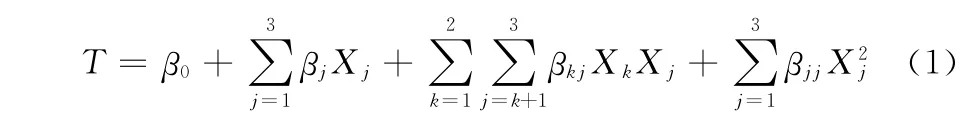
为了应用通用旋转组合试验设计表,还需要对Xj进行编码,即对Xj的试验水平X0j、X1j和X2j进行正交性线性变换:

其中,X0j为Xj的零水平或称为基准水平;Δj表示Xj的变化范围。
确定星号臂长度r:
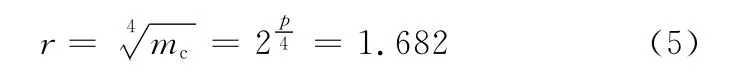
确定总试验次数n:n=mc+2p+m0=20 (6)式中,p为因素个数,这里取3;mc为因子取±1水平的全因素试验的试验次数,其值为2p=8;m0为各因素都取零水平的中心试验的重复次数,这里取6。
确定热板设计参数的变化范围,根据变化范围确定试验点。表1为三因素水平编码表。表2为所得到的二次通用旋转组合试验设计表。

表1 三因素水平编码表

表2 通用旋转组合设计表
3 试验结果分析
3.1 数据的回归分析
针对上述数据,应用SPSS统计软件,用三元二次回归分析的方法进行数据处理,建立回归模型。结果表明,模型的相关系数R为0.985,其平方为0.971,表明其方程的拟合优度好。方差分析的F值的显著性Sig<0.001,所以回归达到显著水平,说明热板表面的温度均匀性T和各因素之间存在显著的回归关系,实验设计方案正确,回归方程有意义。表3为二次回归模型系数表,回归方程为
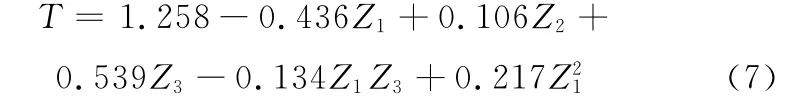
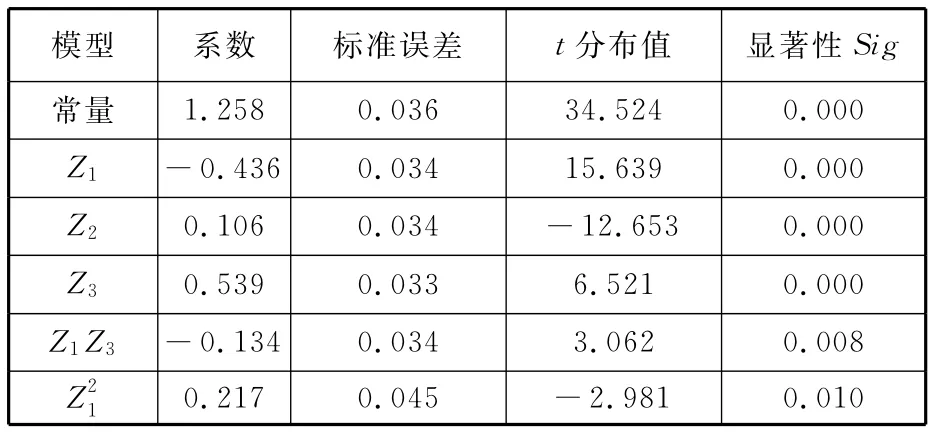
表3 二次回归模型系数表
从表3可看出,对回归方程各项系数进行的t检验表明方程中各项系数在数值上与零差异显著,说明各项系数保留在回归方程中是正确的。
3.2 因子效应分析
回归方程中各因素处理均经量纲一线性编码代换,偏回归系数已经不受因素取值的大小和单位的影响。由于采用通用旋转组合设计方法所得到的回归方程二次项系数间相关,但是各一次项回归系数之间,一次项系数与交互项、平方项的回归系数间都是不相关的,因此,可以用各因素在回归方程中的一次项系数值的大小来比较各因素对热板表面温度均匀性的影响。各因素的作用从大到小依次为:Z3、Z1、Z2,且Z2、Z3是正效应,即Z2和Z3越小,热板表面均匀度越好,T越小。Z1是负效应,即Z1越大,热板表面均匀度越好,T越小。说明结论与经验相符合。对于包括二次项系数的因子效应分析,可以利用各因子间的正交性在正交回归分析中加以讨论。
3.3 回归模型验证
将式(4)代入式(7),得到用自变量Xj表示的回归方程:

对所得回归模型的准确性进行验证,需再进行一次仿真模拟试验,将仿真模拟结果与回归方程计算结果进行对比。分别选取X1为25mm,X2为10mm,X3为10W/(m2·K),代入式(8)得

同样选取上述验证参数值用ANSYS分析软件进行仿真模拟,得到结果为

可以看出,仿真模拟结果与回归模型得出的结果有较高的一致性。通过所建立的回归模型,工程人员可以方便、快捷地了解热板不同设计参数情况下的热板表面温度均匀性。
4 结论
本文给出了一种针对表面温度场均匀性的热板设计参数分析的新方法。通过分析可知,热板表面温度场均匀性影响因素的作用从大到小依次为:Z3、Z1、Z2。所建立的回归模型计算结果与仿真模拟结果有较高的一致性。因为采用的通用旋转组合设计方法能使所得到数学模型回归预测值的方差在以球心为原点的球内为一个常数,所以在热板参数设计中可以应用回归数学模型对不同的参数选择所得结果进行比较,可以使设计过程方便、快捷,具有实际工程应用价值。
[1]Levinson H J.Principles of Lithography[M].2nd ed.Bellingham:SPIE Press,2005.
[2]Schaper C,El-Awady K,Kailath T,et al.Characterizing Photolithographic Linewidth Sensitivity to Process Temperature Variations for Advanced Resists Using a Thermal Array[J].Applied Physics A:Materials Science & Processing,2005,80(4):899-902.
[3]Smith M,Mack C,Petersen J.Modeling the Impact of Thermal History during Post Exposure Bake on the Lithographic Performance of Chemically Amplified Resists[C]//Proc.SPIE 4345.Santa Clara,2011.
[4]Wu C,Hamada M,Wu C.Experiments:Planning,Analysis,and Parameter Design Optimization[M].New York:Wiley-Interscience,2000.
[5]Cain J P,Naulleau P,Spanos C J.Critical Dimension Sensitivity to Post-exposure Bake Temperature Variation in EUV Photoresists[C]//Proc.SPIE 5757.San Jose,2005.
[6]Zhang Q,Friedberg P,Poolla K,et al.Enhanced Spatial PEB Uniformity through a Novel Bake Plate Design[C]//Proc.AEC/APC XVII Symp.Austin,Tx:AEC/APC,2005:1-5.
[7]Chua H,Tay A,Wang Y,et al.A Heater Plate Assisted Bake/Chill System for Photoresist Processing in Photolithography[J].Applied Thermal Engineering,2009,29(5/6):985-997.
[8]Wang L,Loh A P,Gong Z M,et al.An Air-flow Based Wafer Bake System for Improved Temperature Uniformity[J].Journal of Process Control,2008,18(10):931-936.
[9]王建辉,韩邦成.电加热板温度控制的仿真分析[J].光机电信息,2003,20(3):24-27.
[10]刘红,阮灵伟,蒋兰芳,等.基于ANSYS的热板温度场模拟与优化设计[J].模具工业,2010,36(9):18-21.
[11]袁志发,贠海燕.试验设计与分析[M].北京:高等教育出版社,2000.

