探究式教学法在高中数学教学中的应用

于 焱

（大连育明高中，辽宁大连116023）

探究式教学法在高中数学教学中的应用

于 焱＊

（大连育明高中，辽宁大连116023）

培养学生的数学能力，应首先培养学生的创新意识。在数学课堂教学中采用探究式教学法对激发学生学习兴趣、培养学生创新意识有较大的促进作用。

高中；数学能力；创新意识；探究式教学法

高中数学《新课程标准》对数学能力的界定是：数学能力是指以思维能力为核心的空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识。创新意识是数学能力的一个重要方面。创新意识是指学生能够综合与灵活地应用所学的数学知识、思想方法，选择有效的方法和手段分析信息，进行独立思考、探索和研究，创造性地提出问题、分析问题和解决问题。培养学生的创新意识，教学方法的选择至关重要，探究式教学法对于培养学生创新意识有较大的促进作用。

一、探究式教学法的内涵、功能及实施步骤

1.探究式教学法的内涵

探究式教学法是以培养和发展学生的创新意识为目标，从学生已有的数学知识结构和认知结构的特点出发，在教师恰如其分的指导下，通过演示、测量、问题引导等手段，使学生有目的地观察、联想、猜测，相对独立地去发现知识或探求知识的思想方法。

开展探究式教学应把握以下几个方面。首先，教师借助演示、测量、问题引导等手段，对学生进行恰如其分的引导；其次，教师指导、帮助学生有目的观察，进行广泛联想、猜测，相对独立地去发现数学知识或探求数学知识运用的方法；最后，通过发现问题、解决问题，培养和发展学生的数学思维，尤其是培养学生的创造性思维能力。

2.探究式教学法的功能

采用探究式教学法有助于学生成为发现者、研究者、探索者，从而激发学生学习的内在动机；有助于学生养成独立思考的习惯，培养学生成为“自主而能动的思想家”；有助于培养和提高学生思维的整体性、灵活性和独创性；有助于训练学生解决问题的能力、技巧；有助于加深学生对所学知识的理解和记忆。

3.探究式教学法的一般步骤

实施探究式教学法的具体步骤为：提出要求解决或研究的问题；利用已有知识和教师提供的材料进行观察、联想，对提出的问题作出假设（猜想）（前两步在具体实施中是交替出现的）；对所作的假设（猜想）从理论和实践上进行检验（验证）；得出结论。

二、探究式教学法在教学实践中的应用

应用探究式教学法进行教学实践，首先要求教师从整体上了解学生已有数学知识结构和认知结构特点；其次，设问要难度适中，能调动大多数学生的思维；最后，教师必须深入挖掘教材，对教材的一些内容进行重新整合。教师可利用探究式教学法进行公式、定理的教学和教材例题、习题的教学。

1.在公式、定理教学中的应用

例1 推导立体几何中球的体积公式（已知球的半径为R）。

学生已经学习了锥体体积公式的推导方法，这种方法体现的是将几何体分割求体积。为了使学生对此方法体会更深刻，提高学生的创造思维能力，教师可选择推导球的体积公式。

课堂伊始，教师提出问题：如何推导球的体积公式？然后引导学生分析，球是中心对称旋转体，可以先考虑半球，半球有一个底面，易与前面学习过的圆柱、圆锥建立联系。

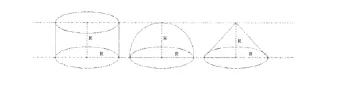
图1

引导学生观察、联想、思考后，教师在黑板上画图，见图1。观察等底等高（底半径为R）的圆柱、圆锥与半球的关系，并设圆柱、半球、圆锥体积分别为V1、V2、V3。由图1可知，三者的大小关系为V1＞V2＞V3，

对V半球做出假设（猜想），学生猜到V2＝。

检验假设（猜想），引导学生探求公式V2＝的证明方法。

在数学课堂上利用探究式教学法的原则、模式及步骤组织课堂教学，能够引发学生对数学知识学习的兴趣，并使他们认识到只要肯动脑筋想办法，就能够自己发现问题、分析问题、解决问题，从而提高思维能力。

2.在例题、习题教学中的应用

课堂教学中，有些教师在例题选择上不太愿意选择教材中的例题，认为它的解法比较简单，而且教材中也有完整的解答步骤。实际上，如果将书中的例题真正讲深将透，能很好地培养学生的创新意识。例2在高考试题中出现的频率较高，而在历年高考试题中都是将它变形后再考学生，但学生得分并不高。这道题在解题方法上可以进行推广，让学生在学习中做一道题能探索出一类题的解题方法。

例2求sin210°＋cos40°＋sin10°cos40°的值。教师要挖掘此例题的潜在因素，对这部分教材进行重新编排，并在教学过程中实施探究式教学法。具体教学步骤如下：

提出问题。遇到平方问题通常怎样入手？学生回答可直接将平方降幂，再和差化积，得出此题答案为。接着，让学生观察另一道类似的题：

求cos273°＋cos247°＋cos73°cos47°的值。

作出假设（猜想）。假设当α＋β＝120°时，

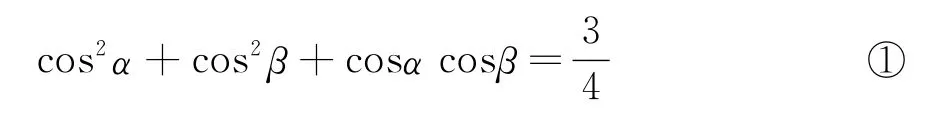
教师又提出问题，若将两道题中的三角函数全部化为正弦函数，能得出什么规律？学生稍加比较后又可得出猜想。假设当α＋β＝60°时，

这两个规律是通过猜想得到的，它们是否完全正确，必须加以论证。

检验假设。引导学生证明假设①（猜想），对假设②（猜想）的证明留给学生课后自己完成。证明：cos2α＋cos2β＋cosαcosβ代入得

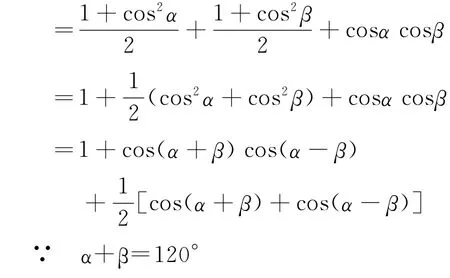
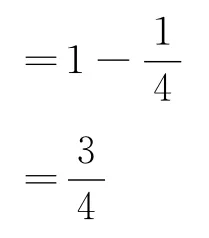
为寻求更一般的规律，教师可以进一步问学生：

当0°＜β＜α＜180°时，是否只有α＋β＝120°时才有①式成立？

提示学生，α＋β＝240°以及α－β＝120°①式是否成立。

引导学生分析前面的推证过程，要使①式成立，只有

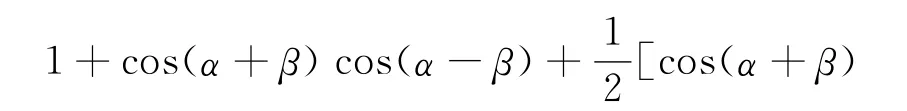
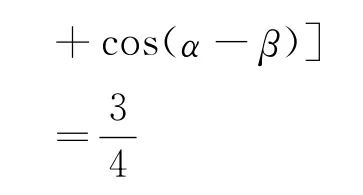
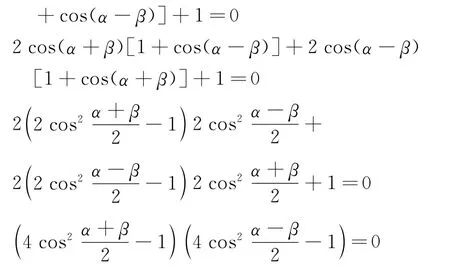
进一步分析，由假设②（猜想）发现：

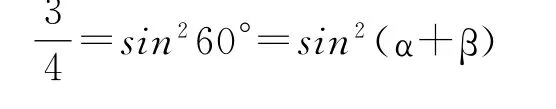
因此假设②（猜想）式可以写成：

当α＋β＝60°时

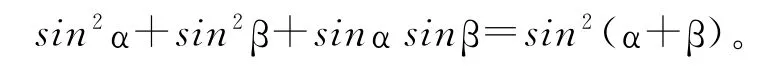
教师又提出问题，如果没有条件的限制，上式能成立吗？如何改变一下式子结构，使它成为一个没有条件限制的恒等式呢？此时学生思维受阻。教师提示，若联想三角形的正弦定理、余弦定理，能否受到启发？这一提示使学生茅塞顿开，有多数学生写出式子，作出猜想，得出假设。

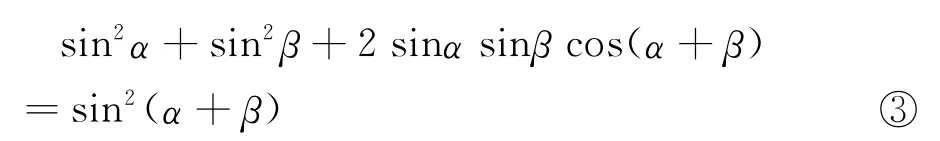
教师又问这个式子是恒等式还是只有在三角形中才成立？

检验假设 ③，引导学生一起证明。

证明：sin2α＋sin2β＋2 sinαsinβcos（α＋β）

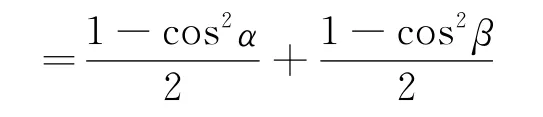
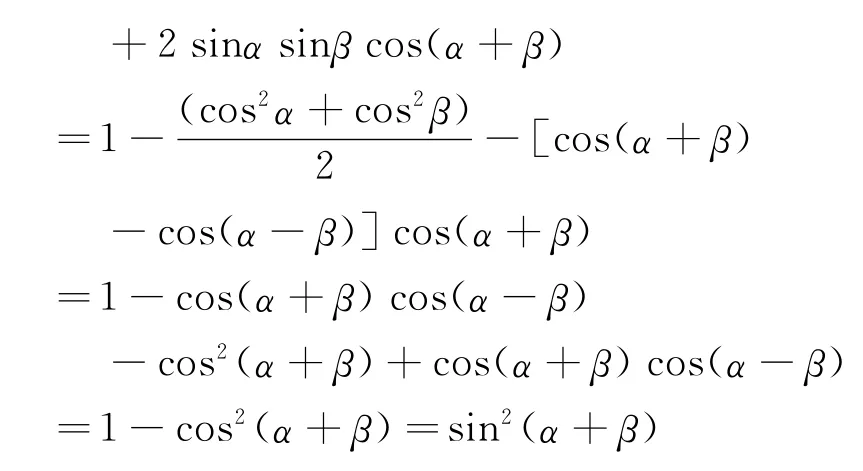
通过证明使学生信服这是一个恒等式。进一步问学生，将③式左边的正弦函数都化为余弦函数后，得出怎么样的结论？仿照以上的方法，学生又得出假设：

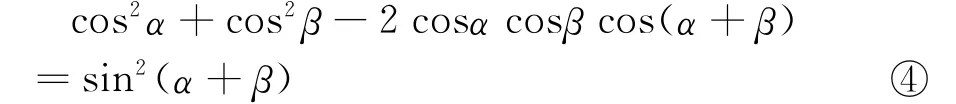
但是否正确没有把握，把假设（猜想）④留给学生课外做。

假设（猜想）③和假设（猜想）④是更一般的关系式，且是恒等式，因此应用范围更广，也更简便。

得出结论。上述4个命题均是正确命题，具体应用如下：

简解，由假设（猜想）①，

原式＝cos270°＋cos250°＋cos70°cos50°

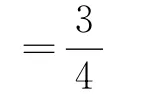
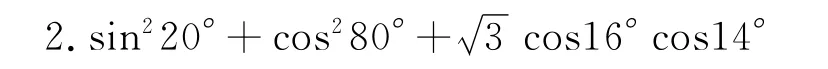
简解，由假设（猜想）③，

原式＝sin220°＋sin210°＋2 sin20°sin10°cos30°

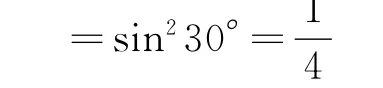
在数学课堂上实施探究教学法，教师除了要吃透教材，研究试题解法的一般规律及定理法则在解题中的引导作用外，还要做到在探索、发现的过程中充分尊重、信任学生，与学生建立一种平等、民主、和谐的关系。同时，教师要不断地向学生提出一些既适合全班学生实际水平又能真正吸引学生的问题，对学生进行恰如其分地引导，让学生自己去观察、联想、猜测，并用已有的数学知识加以检验、证明。这样既能激发学生的好奇心，又能发展学生的个性和创造性，培养学生的创新精神与创新意识，提高学生的数学能力。

［责任编辑：阅力］

On Application of Inquiry－based Teaching Method to High School Mathematics Teaching

YU Yan
（Dalian Yuming High School，Dalian 116023，China）

In order to train students’mathematics ability，we need to train their creative awareness first.In mathematics classroom teaching，inquiry－based teaching method is very useful in arousing students’interest and training students’creative awareness.

high school；mathematics ability；creative awareness；inquiry－based teaching method

book=2012,ebook=64

G633.6

A

1008－388X（2012）02－0020－03

2012－01－12

于焱（1959－），女，辽宁大连人，中学高级教师，特级教师。