对角Ram sey数R（22，23）的新下界

许成章，梁文忠

(1.2.梧州学院，广西 梧州 543002）

对角Ram sey数R（22，23）的新下界

许成章1，梁文忠2

(1.2.梧州学院，广西 梧州 543002）

研究Ramsey数下界的问题，发现了Paley图的一个新的自同构，形成计算Paley图团数的一个新方法，为解决Radziszowski问题提供一个新思路，获得阶段性成果：计算出14813阶Paley图的团数，得到一个对角Ramsey数的新下界：R（23，23）≥29629。

Ramsey数；下界；Paley图；团数；自同构

1 引言

英国数学家F.P.Ramsey[1]在1928年证明了一个定理，后世学者称之为Ramsey定理，相关函数称为Ramsey数，于是确定Ramsey数就成为组合数学中非常困难的问题[2-4]。对于任意给定的整数n≥3，所谓对角Ramsey数R（n,n） 是指满足如下性质的最小正整数r：用两种颜色把r阶完全图Kr的边任意染色后，在Kr中一定有单色的Kr。

人们对Ramsey数R（n,n） 所知甚少。数十年来，各国学者努力探索Ramsey数的上界和下界，试图逐步逼近Ramsey数的准确值.这是涉及到巨量运算的非常困难的一个NP-C问题，任何理论和方法上的创新以及所获得的新成果，都能使人们对Ramsey数加深认识而引起学术界的关注。

关于研究Ramsey数的困难程度，匈牙利数学家Erdǒs说：“需要过上百万年，人们才会得到一些认识，甚至那时也不能达到完全的认识”[3]147。曾任美国数学会主席的Graham猜测人们至少在100年内发现不了 的准确值[3]146。我国数学家李乔说Ramsey数研究的“这个问题是对人类智慧的真正挑战”[3]17。

1947年匈牙利数学家Erdǒs[5]首创概率方法得到对角Ramsey数下界的渐近估计.1955年美国数学家Greenwood和Gleason[6]首创构造性方法，得到历史上第一批Ramsey数的准确值，其中两个对角Ramsey数是这样得到的：首先利用Paley图计算出R（3,3）＞5 和 R（4,4）＞17，再用存在性的方法证明 R（3,3）≤6 和 R（4,4）≤18，就得到 R（3,3）=6 和 R（4,4）=18。

所谓Paley图，是指用4k+1型素数的二次剩余构造的循环图。美国学者Radziszowski的动态综述论文[7]记录了几十年来学术界计算Paley图的团数和研究对角Ramsey数的非常缓慢的进程：直到2002年，罗海鹏、苏文龙等学者方才计算出4457、5501、8941阶的Paley图的团数，得到 R(17，17)≥8917、R(18，18) ≥11005、R(19，19) ≥17885[8]。Radziszowski希望学术界有所创新，推动Ramsey数的研究进展，在http://www.cs.rit.edu/～spr/topics.html中提出如下问题：

“计算20000阶以内的Paley图的团数”。

注意到，用通常的方法计算Paley图的团数，要反复计算大量同构子图，运算效率低下，因而这是非常困难的问题，迄今尚未见有文献报道这个问题的研究进展。笔者发现了Paley图的一个新的自同构，能够减少大量同构子图的重复计算，改进了计算对角Ramsey数的方法，用计算机探索得到一个尚未见有文献报道的新成果。

2 Paley图的二级导出子图及其自同构

设p≥29是4k+1型素数，Zp=｛-2K,…,-2,-1,0,1,2,…,2K｝是有限域，约定以下所有运算结果都在模P同余的意义下归结到Zp。

定义1 设A是由模P的平方剩余形成的集。无向简单图Gp称为Paley图，其顶点集V(Gp)=Zp，边集

引理 A[9]设 B= ｛x｜x∈A，x-1∈A｝，Gp在 B上的导出子图记为Gp[B]，则Gp[B]有如下六个自同构：f0(x)=x，f1(x)=x-1，f2(x)=1-x-2，f3(x)=x(1-x)-1，f4(x)=x(1-x)-1，f5(x)=1-x，其中x∈B。

上述自同构确定的等价关系“～”把B分拆成如下若干个等价类。其中代表元是α的等价类记为〈a〉各等价类代表元形成的集记为N 。

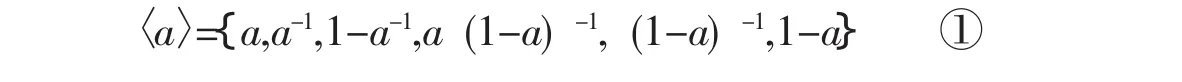
引理 B[8]｜B｜= （p-5）/4。设 S=｜B｜mod 6，则有S=0，2，3，5四种情形。B1中的等价类一般都是如①所示的6元集，当且仅当S=0时B中的等价类都是6元集，当且仅当 S=2或S=3时在B中有一个S元等价类，当且仅当S=5时在B中有一个2元等价类和一个3元等价类。

不妨把上述所说的导出子图、自同构和等价类分别称为一级导出子图、一级自同构和一级等价类，本文在此基础上引进图的二级导出子图、二级自同构、二级等价类等新概念。

定义 2 设 B1=B=｛x｜x∈A,x-1∈A｝ ≠○，A a∈B1，令 B2= ｛x｜x∈B1,x-a∈A｝，称a为B2的导出元，B2为a的导出集。

定理1 设a∈B1是B2的导出元，令

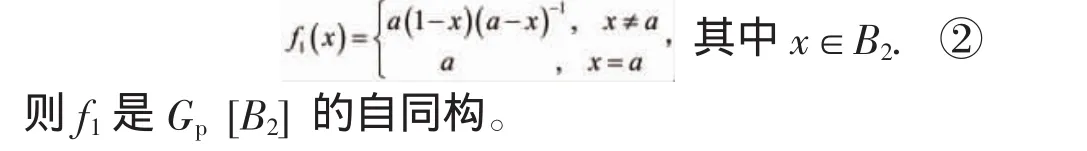
证明 易知f1作成Zp的一个置换。注意A到a∈B1∪A，由 B1，B2，f1的定义与 A 的性质，x，y∈B1∪A，当 xy≠0 时有

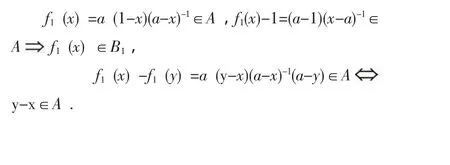
3 全序“ ”与B2的改进

4 计算Paley图团数的一个新方法

我们运用一般的计算机完成上述两例的计算，耗时不到1s.

5 主要结果

在CPU为Intel·i3/2100的计算机上，我们完成上述运算大约耗时70h。

[1]Ramsey F P.On a problem of formal logic[N].Proceedings of the London Mathem aticalSociety,1930,30:264～286.

[2]R.L.Graham,B.L.Rothschild,J.H.Spencer.Ram sey theory[M].JohnWiley&Sons,1990.

[3]李乔.拉姆塞数理论[M].长沙:湖南教育出版社.1991.

[4]李乔.组合数学基础[M].北京:高等教育出版社,1993.

[5]P.Erd·s.Some remarks on the theory of graphs[J].Bulletin of the American Mathematical Society,1947,53:292～294.

[6]R.E.Greenwood and A.M.Gleason,Combinatorial relations and chromatic grap hs[J].Canadian JournalofMathematics,1955(7):1～7.

[7]S.P.Radziszowski.Small Ramsey Numbers[J].The Electronic Journalof Combinatorics,View the Journal,Dynam ic Surveys,2011,August22 ElJC revision#13,2011,DS1.13:1～84

[8]Luo Haipeng,SuWenlong,Li Zhengchong.The properties of self-complementary graphsand new lower bounds for diagonal Ramsey numbers[J].Australasian Journal of Combinatorics,2002(25):103～116.

[9]SuWenlong,Luo Haipeng,LiQiao,Lowerbounds formulticolor Classical Ramsey Numbers[J].Science in China(seriesA),1999,42(10):1019～1024.

New Lower Bounds for Diagonal Ram sey Numbers R（22，23）

Xu Chengzhang1,Liang W enzhong2
(1.2.W uzhou University,W uzhou 543002,China)

The paper studies the lower bounds for Ramsey numbers.In light of a new discovery automorphism of Paley Graphs,a new method of computing clique numbers of Paley graphs is proposed,which sheds new light on solving the problem raised by Radziszowski.Staged results are obtained:the clique number of Paley graphs with order 14813 is computed and a new lower bound for diagonal Ramsey numbers R（23，23）≥29629 is obtained.

Ramsey number;lower bound;Paley graph;clique number;automorphism

O157

A

1673-8535（2012）02-0075-06

许成章（1976－），男，广西梧州人，梧州学院讲师，研究生，主要研究方向：图论、组合数。

梁文忠（1963－），男，广西贺州人，梧州学院副教授，研究方向：组合数学的研究。

（责任编辑：高 坚）

2012-01-12

国家自然科学基金资助项目（60563008）；广西自然科学基金项目（0991278）；广西教育厅科研项目(200911LX433)；梧州学院科研项目(2009B013，2009B011)资助