提高线性代数课堂教学效果的几点体会

陈 红，黄 劲

（1.2.梧州学院 数理系，广西 梧州 543002）

提高线性代数课堂教学效果的几点体会

陈 红1，黄 劲2

（1.2.梧州学院 数理系，广西 梧州 543002）

线性代数是理工科重要的基础课程，结合教学实践以及一些思考，从线性代数的课程主线、概念教学、技能培养、思想方法等方面，就如何提高线性代数课程教学效果的谈几点体会。

线性代数；课程主线；概念；技能；思想方法

线性代数是理工科和部分文科专业重要的基础课程，它是自然科学和社会科学的基本工具，它的理论和方法无论是对学生知识结构的完善还是对学生综合素质的提高以及创新能力的培养都有着十分重要的作用。线性代数教学效果直接影响着学生在实践中应用数学的能力。

线性代数课程的特点是学时少、概念多、抽象度高、思维方式独特。由于该课程理论性强,技能性强，教师在教学过程中既要保证数学原理的传授，又要使学生及时掌握主要的解题方法，两者往往难以平衡。特别是某些章节由于理论多、晦涩难懂，学生感到学线性代数像是“读天书”，甚至有些老师在有关这些内容讲授时采取只介绍结论,不去讲授其原理的短平快教学模式，从而影响了教学效果，也达不到教学的目的,以至于学生陷入迷茫之中。本文以同济大学编写的《线性代数》[1]教材为研究对象，结合教学实践以及一些思考，就如何提高线性代数的教学效果谈几点体会。

一、以线性方程组解的理论为课程主线，以线性空间、线性变换为方向组织教学

“线性代数”是一门“空间为体，矩阵为用”（即用矩阵理论研究向量空间及其线性变换）的课程[2]。如果从主攻课题和研究方法的角度来分析,线性代数是以线性方程组解的理论和方法为起点,研究线性空间及其上线性变换的不变量理论的课程，其主要工具是矩阵理论。现行主流的线性代数课程大抵包括以下一些内容：行列式、矩阵、向量、线性方程组、特征值特征向量、二次型、线性空间和线性变换。线性代数每一章研究的对象、概念不能在前一章的基础上建立起来，从这个角度来说各章之间的关联性不强，学生每一章都要重新学习新概念的定义、性质、相关计算及一系列结论。造成学生感觉刚刚初步熟习一个内容，接着又出现了新的研究对象，一个难题接一个难题，没有一个课程主线，这是线性代数难学的原因之一。根据线性代数这一特点，确定以线性方程组解的理论为课程主线，以线性空间、线性变换为方向组织教学。该方法避免了学生学习的盲目性,带着问题看每一个新的研究对象，知道为什么要引进这个概念及研究这个概念的数学背景，这样新的概念就变得似曾相识了，提高了教学效果。

1．以线性方程组解的理论为课程主线组织教学客观世界的数量关系中线性问题（即均匀化的问题）可以列出线性方程组求解。计算机的迅速发展使得成千上万个未知量的线性方程组也有可能求解，这需要给出统一的、机械的求解线性方程组的算法。含n个未知量的线性方程组称为n元线性方程组，它的一般形式为：

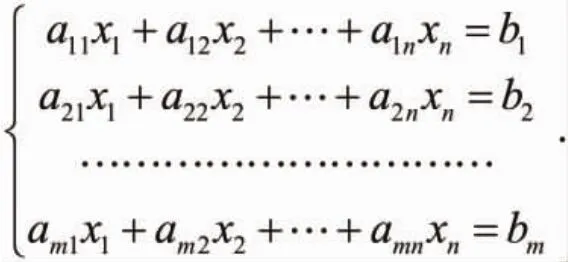
问题：线性方程组是否有解？有解时，有多少个解？如何求线性方程组的解？线性方程组的解不止一个时，这些解之间有什么关系？

特殊情形:当方程个数与未知量个数相等时，即m=n时，从二元、三元线性方程组入手，得出它们的公式解，引出二阶、三阶行列式。对于n个方程的n元线性方程组有没有类似的结论呢？引出n阶行列式的概念，最后得到克莱姆法则：如果系数行列式，则方程组有唯一解。

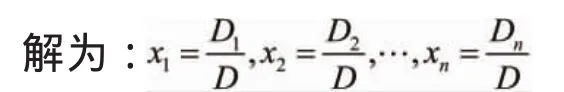
克莱姆 (Cramer)法则直接从线性方程组的系数和常数项求出方程组的解。

问题：（1）当D=0时，克莱姆法则失效，无法判定无解和有无穷多解的情形，如何求解？

（2） 当方程个数与未知量个数不相等时，即m≠n时，克莱姆法则失效，因此需要进一步研究一般的线性方程组如何直接从它的系数和常数项判断它有没有解，有多少解，有解时如何求出它的解？

解决方法：分析解线性方程组的Gauss消元法，我们看到求解过程中只是对线性方程组的系数和常数项进行了运算，于是利用矩阵、矩阵的初等行变换来解线性方程组，从而引出了矩阵的内容。下面通过例子说明如何从“矩阵”过渡到“向量”。

问题：线性方程组的有无穷多解时，解与解之间有什么关系？其解集的结构如何？

解决方法：引入向量，定义向量的线性运算。讨论向量之间的关系，即向量组、向量的线性表示、向量组的线性相关性、最大无关组、向量空间的概念。

齐次线性方程组的解集 S｛x｜Ax＝0｝是一个向量空间（称为齐次线性方程组的解空间，它是Rn的子空间），解向量组的一个最大无关组称为方程组的基础解系，它即是解空间的基。由此得到齐次线性方程组的解集的结构，从而得到非齐次线性方程组的解集的结构，到此，线性方程组的问题得到彻底解决。

接下来特征值、特征向量是解线性方程组的应用，二次型是行列式、矩阵、解线性方程组的综合应用。

以如何解线性方程组为主攻课题组织教学，重现了线性方程组理论问题的研究过程和创新过程，随着问题的讨论深入，不断地引进新的概念及相关理论，使学生在发现问题、解决问题的过程中搭建起线性代数的知识结构，学习并逐渐掌握行列式、矩阵、向量空间的理论和方法。实践表明这种以问题为中心组织教学的方法，能够引起学生的注意，激发学生学习的主动性，有利于在教学过程中促进学生的泛参与，取得了较好的教学效果。

2．以线性空间、线性变换为方向组织教学

研究线性方程组的解法、解的情况的判别和解集的结构时，贯穿了研究n维向量空间Rn及其子空间这条主线。为使向量及向量空间的概念更具一般性，于是引入了线性空间的概念。

问题：如何在n维向量空间Rn的基础上研究Rn维线性空间Vn？

解决方法：引入线性空间的维数、基、坐标及同构的概念。

设 α1,α2,…,αn是 n 维线性空间 Vn的一组基，在这组基下，Vn中每一个向量都有唯一的坐标 (x1,x2,…xn)T，因此Vn与Rn之间就建立了一一对应关系。设 α=x1α1+x2α2+…xnαn+，β＝y1α1+y2α2+…ynαn，即α，β的坐标分别是 (x1,x2,…xn)T， (y1,y2,…yn)T，那么

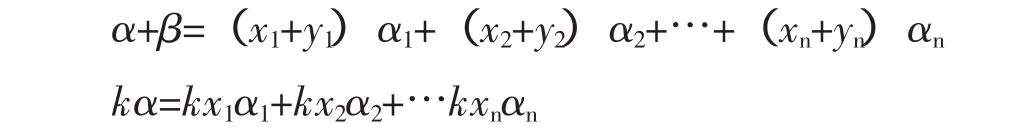
于是 α+β，kα 的坐标分别是 （x1+y1，x2+y2，…，xn+yn），（kx1，kx2，…，kxn）T这表明向量用坐标表示后，Vn中的抽象的线性运算可转化为Rn中的线性运算，Vn的讨论就可归结为Rn的讨论。给出线性空间同构的概念，得到任何一个n维线性空间Vn都与Rn同构，即维数相等的线性空间都是同构的。

在线性空间的抽象讨论中，不考虑线性空间的元素是什么，也不考虑其中的运算是怎样定义的，而只涉及线性空间在所定义的运算下的代数性质，从这个观点来看，同构的线性空间可以不加区别，因此，维数是有限维线性空间的唯一本质特征，是有限维线性空间的不变量。特别地，每一个n维线性空间Vn都与Rn同构，而同构的线性空间有相同的线性性质，由此可知我们前面对Rn的研究中，凡是只涉及线性运算的性质及有关结论（如线性组合、线性相关、线性无关、最大无关组、向量空间的基和维数、向量的坐标、基变换、坐标变换、过渡矩阵等）在一般的n维线性空间Vn都是成立的。因此，n维向量空间Rn是n维线性空间Vn的一个具体模型，因此，有限维线性空间的结构可以认为是完全清楚了。

矩阵的研究为线性变换的研究打下了基础。

问题：如何用矩阵研究线性变换？

解决方法：引入线性变换的矩阵的概念，线性变换与n阶方阵之间建立一一对应关系。

在n维线性空间Vn中取定一组基后，线性变换可用矩阵表示，线性变换与n阶方阵之间就建立了一一对应关系，且这个对应保持运算，即线性变换的和、乘积、数量乘积、分别对应于矩阵的和、乘积，数量乘积，且可逆线性变换对应于可逆矩阵，逆变换对应于逆矩阵。线性变换的核心问题是寻找一组合适的基，在这组基下线性变换的矩阵具有最简单的形式，其本质上就是研究相似矩阵的问题。线性变换的值域的维数就是其对应的矩阵的秩，以线性变换对应的矩阵为系数矩阵的n元齐次线性方程组的解空间的维数公式本质上线性变换的核与值域的维数公式。

数学问题解决是一种研究性教学模式。学习者首先面对问题，教师引导学生以问题为中心或者诱因，选用解决问题的策略，构建数学知识，提高数学能力。学习者在学习过程中能够获得更为丰富的建立在更科学的基础上的经验，从而产生更多的体验,有利于学生感悟如何提出问题，知道何时对问题进行分析,如何寻求帮助,并且收集足够的信息来解决问题；这种学习方式有利于学生养成一种主动探究和解决问题的习惯[3]。事实上，科学研究往往是先确定要做什么？然后考虑如何做？通过引入重要概念搭桥，最终对问题加以解决。

以线性方程组解的理论为课程主线，以线性空间、线性变换为方向组织线性代数的教学，能使学生在获得知识、技能的同时体会到数学的思想方法，培养了学生的问题意识、创新意识，增强了学生探索问题、解决问题的能力。

二、注重关键概念的教学

关键概念指的是通过对教学内容的理解提炼出某章或某节的能贯穿教学内容的概念。线性代数知识点多、抽象性强、概念关系错综复杂，只有在正确理解概念的基础上才能更好地理解线性代数的思想方法，从而掌握线性代数的重要定理和结论。因此，教学中更要重视基本概念的教学，特别是加强关键概念的教学。

例如：向量组的线性相关性这一章主要围绕五个关键概念展开：向量组的线性相关性（线性相关、线性无关）、向量组的最大无关组、向量组的秩、矩阵的秩、齐次线性方程组的基础解系。这五个关键概念环环相扣，把这一章的教学内容串联起来。其中向量组的最大无关组是连接其他四个概念纽带，它的定义如下：

定义 设有向量组A，如果在A中能选出r个向量 α1,α2,…,αr，满足

（i）向量组A0：α1,α2,…,αr线性无关；

（ii）向量组A中任意r+1个向量（如果A中有r+1个向量的话）都线性相关。

则称向量组A0是向量组A的一个最大线性无关向量组（简称最大无关组）。

由此看到，最大无关组是向量组线性相关性的核心。另一方面，最大无关组给出了向量组的秩和矩阵的秩含义，向量组的秩等于向量组的最大无关组所含的向量个数，矩阵的秩等于它的列向量组的秩，也等于它的行向量组的秩。齐次线性方程组的基础解系即是它的解向量组（或解空间）的最大无关组。

教学中，对每个关键概念都要使学生深刻理解概念的内涵，理清它与其他概念的区别与联系，及时建立概念体系。如向量组的线性相关、线性无关定义如下：

定义 给定向量组 A：α1,α2,…,αs，如果存在不全为零的数 k1,k2,…,ks使 k1α1+k2α2+…+ksαs=0，则称向量组A是线性相关的，否则称向量组A线性无关。

这是形式化语言给出的定义，学生感觉抽象难学。首先可以通过简单的例子理解概念的内涵。

向量组 α1,α2,…,αs是线性无关如果从 k1α1+k2α2+…+ksαs=0 可以推出系数 k1=k2=…=ks=0。

然后把线性相关、线性无关的概念与其他概论和知识点联系起来，多角度多方面思考问题，使得对这个概念的理解逐步完善和充实，并获得其它判断和求解方法。

（1） 从齐次线性方程组的角度α1,α2,…,αs线性相关齐次线性方程组 x1α1+x2α2+…+ksαs=0 有非零解。α1,α2,…,αs线性相关齐次线性方程组 x1α1+x2α2+…+ksαs=0 只有零解。

（2） 从线性组合的角度α1,α2,…,αs线性相关存在不全为零的组合系数使得线性组合等于零向量。α1,α2,…,αs线性无关只有组合系数全为零的线性组合才能等于零向量。

（3）线性表示的角度

向量组 α1,α2,…,αs线性相关其中至少有一个向量可以由其余向量线性表示。

向量组 α1,α2,…,αs线性无关其中每一个向量都不能由其余向量线性表示。

（4）从行列式的角度

n 个 n 维列 （行） 向量 α1,α2,…,αn线性相关以 α1,α2,…,αn为列 （行） 向量组的矩阵的行列式等于零。

n 个 n 维列 （行） 向量 α1,α2,…,αn线性无关以 α1,α2,…,αn为列 （行） 向量组的矩阵的行列式不等于零。

（5）从矩阵的秩的角度

α1,α2,…,αs线性相关以 α1,α2,…,αs为列向量组构成的矩阵的秩小于S

α1,α2,…,αs线性无关以 α1,α2,…,αs为列向量组构成的矩阵的秩等于S

如果一个向量组的一个部分组线性相关，那么整个向量组也线性相关。

如果向量组线性无关，那么它的任何一个部分组也线性无关。

采用这样的教学方法，加深了学生对概念的理解，培养了学生全面思考、多方位、多角度看待事物的能力，同时把尽可能多的知识联系起来，便于学生记忆和理解更多的知识。

线性方程组一章中，五个关键概念之间的关系是：向量组的线性相关性→向量组的最大无关组→向量组的秩→矩阵的秩→线性方程组的基础解系。其中最大关组是连接其他关键概念的纽带。教学中结合例题，培养学生综合应用概念解决问题的能力。例如，有关矩阵的秩的证明题，由于其太抽象学生往往无从下手，但若利用矩阵的秩与向量组的最大无关组这两个关键概念的关系来证明则可使思路清晰。

例 证明 R（A+B）≤R（A）+R（B）

证明 设A、B的列向量组分别为：α1，α2，…，αn；β1，β2，…，βn，则 A+B 的列向量组为 α1+ β1，α2+β2，…，αn+βn，设 αi1，αi2，…，αir是向量组 α1，α2，…，αn的一个最大无关组；设 βj1，βj2，…，βjt是向量组 β1，β2，…，βn的一个最大无关组。则 α1+ β1，α2+β2，…，αn+βn可由向量组 αi1，αi2，…，αir，βj1，βj2，…，βjt线性表出。因此

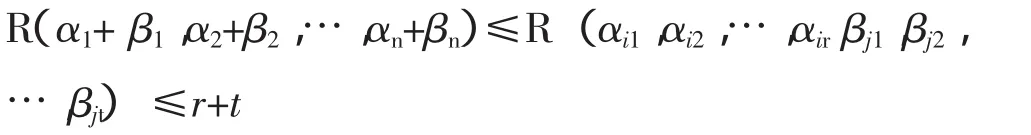
于是 R（A+B）≤R（A）+R（B）。

例题的证明过程中运用了最大无关组的性质、矩阵的秩与构成它的列向量组的秩的关系，以及向量组的秩与其最大无关组所含向量个数之间的关系，使问题通过最大无关组这个纽带得以证明。

三、注重培养学生的“线性代数”技能

数学技能是学生在数学学习过程中通过训练而形成的一种心智活动方式[4]。

教学过程中，要重视计算行列式、求矩阵的秩、求逆矩阵、解方程组、讨论向量组的线性相关性、求方阵的特征值和特征向量等线性代数基本技能的训练，及时总结解题方法和解题步骤。数学技能的形成必须以良好的知识结构为基础，以对知识的理解为前提。而学生在数学技能学习和熟练的过程中又可以加深对知识的理解，促进知识结构的进一步完善。

例如学生要熟练掌握求矩阵的特征值和特征向量的技能。首先，必须理解矩阵的特征值、特征向量、特征多项式和特征方程的概念，确定求矩阵的特征值和特征向量的解题步骤：（1） 写出｜λEA｜特征多项式 ； （2） 求出｜λE-A｜＝0 的特征方程的全部根，即得矩阵A的全部特征值λ1，λ2，…，λn；（3） 将每个特征值 λ＝λi代入齐次线性方程组（λE-A）x＝0，求其基础解系，基础解系的线性组合（零向量除外） 就是A对应于特征值λi的全部特征向量。其次，根据教师对例题的讲解示范，模仿着写出求一个矩阵的特征值和特征向量的过程；然后根据模仿和自己的理解，重复例题的过程；并在这个过程中逐渐体会和加深理解特征多项式、特征方程、特征值、特征向量等概念和具体的解题步骤；最后通过一定量的课后练习达到熟练掌握的程度。

四、注重突出“线性代数”思想方法

数学思想方法包含在数学知识之中，是数学知识发生过程的提炼、抽象和概括，是对数学规律的认识。所以应该把数学思想方法的培养与数学知识的教学融为一体。教学中不仅要传授线性代数的知识和技能，还要帮助学生逐渐掌握具有“线性代数”特点的思想方法，如矩阵法、变换法、向量法等思想方法，了解影响代数学发展的全局性方法：公理化方法、结构化方法和等价分类方法。

例如：矩阵是研究向量空间及其线性变换的主要工具，在教学中一方面要使学生学会把各种问题转化成矩阵问题，另一方面要教会学生熟练掌握矩阵理论和方法，特别是矩阵的初等变换和矩阵的乘法。

再例如：数、多项式、矩阵、向量等具体的数学对象构成的集合，关于各自加法和数乘都满足的八条运算律，都构成代数体系。把这种具有共同本质的代数体系集中起来，抽掉它们的元素所表示的具体含义，抽象出统一的代数结构，寻找它们的共同规律。于是用公理化方法，把八条运算律作为公理给出线性空间的定义。对于刚入大学的学生来说，线性空间是他们遇到的第一个用公理来定义的抽象概念，同时也是他们接触到的第一个代数结构。采用结构化方法，依据线性空间的公理化定义来研究线性空间中元素之间的关系、线性空间和它的子空间的关系、线性空间的生成方法、线性空间的分类等问题。经过研究我们发现，同一数域F上的线性空间可以有不同的代数结构，这里的本质是线性空间的维数。对于同一数域F上的线性空间而言，在同构意义下维数相同的线性空间有相同的代数结构，“同构”是线性空间之间的一个等价关系，用这个关系可以按“维数相等”把线性空间进行分类。因此，在同构的意义下数域F上的n维线性空间只有一个。

这种把具有共同本质的代数体系集中起来，抽象出它们共同的代数结构，统一用代数结构的思想、方法、语言去研究和描述客观世界的方法是代数学中常用的方法。另一方面，研究线性空间中笔者用了公理化方法、结构化方法和等价分类方法，这种宏观性的数学方法贯穿于代数学各分支的始终，在教学中要明确告诉学生。

[1]同济大学数学教研室．工科数学：线性代数[M]．5版．北京：高等教育出版社，2007．

[2]李尚志．线性代数教学改革漫谈[J].教育与现代化，2004(1):30-33．

[3]褚小婧,程向阳.大学数学研究性教学的实质及探索[J].大学数学,2011(1):16-20

[4]马忠林.数学学习论[M].南宁:广西教育出版社,1997:16.

On Im proving Teaching Effectiveness of Linear Algebra Course

Chen Hong1，Huang Jin2
(1.2.Department of Physics and M athematics,W uzhou University,W uzhou 543002,China)

Linear Algebra course is one of the basic courses for science and engineeringmajors.Based on the author's own teaching experience and reflection,the paper discusses how to improve the teaching effectiveness of the linear algebra course in the aspects of themain thread of the course,concept teaching,skills development,ways of thinking,etc.

linear algebra;main thread of the course;concept;skills;ways of thinking

G642.4

A

1673-8535（2012）02-0087-06

陈红（1962-），女，梧州学院副教授，硕士，研究方向：组合数学。

黄劲（1964-），男，梧州学院数理系讲师，研究方向：概率论与数理统计。

（责任编辑：高 坚）

2012-02-12

新世纪广西高等教育教学改革工程项目(2011JGB128)；梧州学院教育教学改革工程资助项目(WyjgB002，Wyjg2010A008)