导数在解决函数问题中的应用

☉浙江省上虞市上虞职教中心 陈 轶

导数是解决函数的单调性、极值、最值、切线等问题的有力工具，作为高中数学的新增内容之一，运用导数研究函数的恒成立、最值、方程、不等式的证明等问题是近几年高考的热点，也将是命题的新增长点.如果给定函数解析式次数高于二次、形式复杂时，常考虑用导数解决函数问题.

一、利用导数解决函数单调性问题

当函数的表达形式复杂、用初等函数不能求解时，常考虑用导数的方法求解.通常先由导数公式求出f′（x），解关于f′（x）的不等式时注意分类讨论的思想.

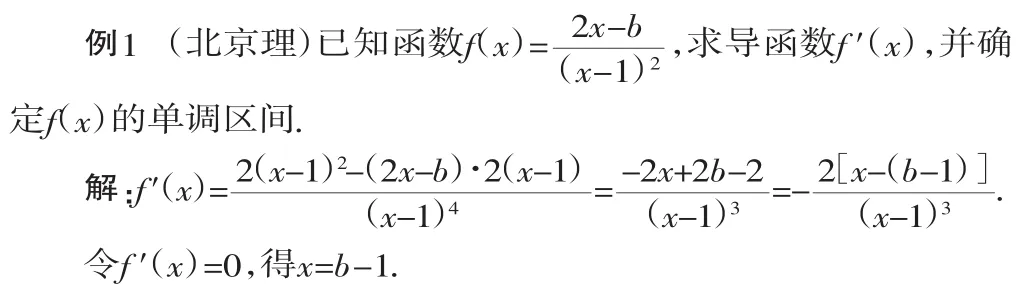
当b-1<1，即b<2时，f′（x）的变化情况如下表：

x （-∞，b-1） b-1 （b-1，1） （1，+∞）f′（x）-0+-

当b-1>1，即b>2时，f′（x）的变化情况如下表：

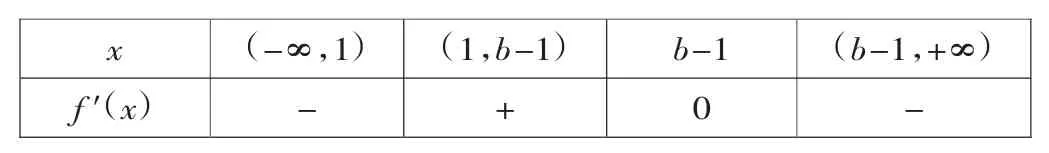
x （-∞，1） （1，b-1） b-1 （b-1，+∞）f′（x）-+0-

当b<2时，函数f（x）在（-∞，b-1）、（1，+∞）上单调递减，在（b-1，1）上单调递增；

当b>2时，函数f（x）在（-∞，1）、（b-1，+∞）上单调递减，在（1，b-1）上单调递增；

点评：求导后的分类讨论问题应注意：一要找分类点（根的大小比较、含x的最高次项系数正负的确定）、列表；二要结合代数方法（如分解因式、配方法、解方程或不等式，处理导函数的正负问题.

二、利用导数解决函数的最值问题

对闭区间的可导函数求其最值时，先求出函数的极值，再比较端点值的函数值与极值的大小，从而确定出函数的最大值、最小值.

（1）求函数f（x）的单调区间.

（2）设g（a）为f（x）在区间［0，2］上的最小值.

（i）写出g（a）的表达式；

（ii）求a的取值范围，使得-6≤g（a）≤-2.

若a≤0，则f′（x）>0，f（x）的单调递增区间是［0，+∞）.

点评：本题主要考查函数的性质、求导、导数的应用等基础知识，同时考查分类讨论思想.立足基础，解决问题，突出导数的工具性.

三、利用导数解决函数的恒成立问题

恒成立问题是近几年的热点，一般有两种典型结构：“a≤f（x）恒成立”、“a≥f（x）恒成立”.解决的方法是求f（x）的最小值m或最大值M，将问题转化为“a≤m”或“a≥M”.尤其要注意端点值的取舍问题.

设g（x）=2（1+x）ln（1+x）-x2-2x，则g′（x）=2ln（1+x）-2x.

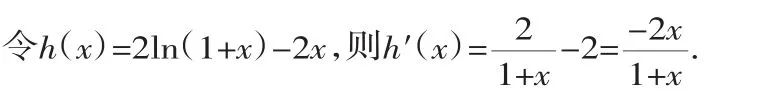
当-10，h（x）在（-1，0）上为增函数.

当x>0时，h′（x）<0，h（x）在（0，+∞）上为减函数.

所以h（x）在x=0处取得极大值.h（0）=0.

所以g′（x）<0（x≠0），函数g（x）在（-1，+∞）上为减函数.

于是当-1g（0）=0，当x>0时，g（x）

所以，当-10，f（x）在（-1，0）上为增函数.

当x>0时，f′（x）<0，f（x）在（0，+∞）上为减函数.

故函数f（x）的单调递增区间为（-1，0），单调递减区间为（0，+∞）.

点评：本题寻找恒成立的方法是通过两边取对数化指数问题为对数函数问题，分离参数转化为“a≤f（x）恒成立”的类型，利用第一问中结论证明G′（x）≤0恒成立，进而借助函数单调性寻找其最小值大于a成立，手法新颖，突破了常规 .

四、利用导数解决切线方程问题

利用导数求曲线的切线方程，关键是求出切线的切点和斜率，方法是设出切点坐标，由导数公式求出切线斜率.

例4 （湖北文）已知函数f（x）=x3+mx2-m2x+1（m为常数，且m>0）有极大值9.

（1）求m的值；

（2）若斜率为-5的直线是曲线y=f（x）的切线，求此直线方程.

解：（1）由f′（x）=3x2+2mx-m2=（x+m）（3x-m）=0，得：x=-m或

当x变化时，f′（x）与f（x）的变化情况如下表：

x （-∞，-m） -m -m，1 3（ ）m 1 3m 1 3m，+∞（ ）f′（x）+0-0+f（x）↗极大值↘极小值↗

从而可知，当x=-m时，函数f（x）取得极大值9.

即f（-m）=-m3+m3+m3+1=9.解得m=2.

（2）由（1）知，f（x）=x3+2x2-4x+1，依题意知f′（x）=3x2+4x-4=-5.

即5x+y-1=0或135x+27y-23=0.

点评：利用导数求曲线的切线方程几乎是每年高考必考的内容，关键是利用导数求出切线的斜率，确定切点坐标.

总之，利用导数研究函数的单调性、最值、恒成立、方程等问题 ，充分论证了导数的工具作用.导数把图形中的信息表达为代数信息，实现了数与形的和谐统一，使问题的解决更加简单清晰.