高中数学概念教学『三部曲』

☉江苏省启东市吕四中学 许红卫

高中数学概念教学『三部曲』

☉江苏省启东市吕四中学 许红卫

新课标强调学生是教学的主体，倡导体验式和探究式教学，因此，数学概念的教学过程应注重学生的本位性，重视学生在概念学习中从感性到理性的过程体验，在体验中学习概念，深化对概念内涵、外延的理解，提升学生概念的内化程度．那么按照新课程的理念，高中数学概念教学应当如何施展呢？笔者认为概念教学应踏好节奏，下面结合教学实例浅谈几点做法．

一、“课堂启动”——概念教学问题化

数学概念是构成高中数学知识大厦的基石，学生概念理解上的缺失势必导致数学思想方法和解决实际问题的贫瘠化，传统教学模式中直接灌输的多，学生还没有准备好，还没有能够进入思考状态，教师就将枯燥的符号和公式呈现在学生的面前，导致学生学习兴趣的低落，更谈不上探究欲望的激发．理论分析和实践经验表明，课堂需要一个启动的过程，即需要在课堂伊始从学生的最近发展区出发创设教学情境，课堂启动的过程是引起学生注意、促使其融入情境的过程，笔者在教学实践中注重以问题为中心，概念教学问题化，将教学目标分解为几个具体任务来驱动整个概念的教学．

例如，“直线与圆的位置关系”这一概念的导入，笔者从学生的原有认知基础出发，设置如下几个问题：

（1）从原有的概念中回忆一下，两条直线存在着哪些位置关系?

（2）两条直线的位置关系可以用哪些方程来表示?

（3）试想一下，直线与圆存在哪几种位置关系?

（4）如何对直线与圆之间的位置关系进行判定？你能想到什么方法?

在问题情境的创设上，在对上述几个问题的处理上，笔者借助多媒体将直线与圆的位置关系的一些图形进行了动态演示，最大限度地提高学生的感性认识，引导学生的思维向着更为广阔的方向发展．

再例如，“映射与函数”这一概念的导入，笔者从现实生活中取景进行情境的创设：汽车进入了千家万户，一个实际的问题自然生成“现在车管所在对车辆管理上，如何做能够确保管理的有效性？”

笔者在提出这个实际问题后，学生的兴趣和注意力立刻被转移过来了，答案亦是学生熟知的，即给每一辆车配个“身份证”，即“上牌照”，不同的汽车有一个不同的号码与之对应！接着由此类推，设置几个与“映射”概念相关的小问题，通过对问题的回答让学生获得一定的感性认识，学生对概念的第一印象就尤为深刻，有利于其在接下来的探究过程中学习能动性的充分释放.

二、“课堂加速”——概念形成过程化

概念学习的过程是一个从未知到已知的探究过程，在具体学习中应从学生的最近发展区出发，结合知识的特点，加强直观教学，由具体到抽象，适当地“加速”，拾级而上，通过教师情境的设置和问题的牵引，让学生从感性到理性体验概念构建的过程.

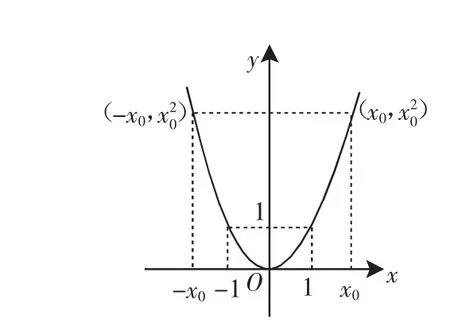
图1

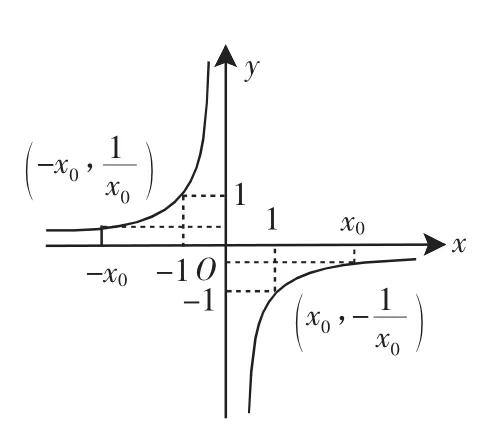
图2

例如，“函数的奇偶性”一节概念课教学中，笔者首先借助多媒体投影了如图1、图2所示的两个函数图像.引导学生对图像进行观察，自己去发现图中两个函数的特征（图1关于y轴对称，图2关于坐标原点对称），在此发现的基础上，笔者投影出问题：

结合两幅图形，看看f（－1）与f（1）、f（－2）与f（2）、f（－3）与f（3）…存在着怎样的关系，并归纳出两个函数在代数形式上的特征（图1可表示为f（－x）=f（x）；图2可表示为f（－x）=－f（x）），完成从图像表征向符号表征的转化，对这两类函数进行定义和区分的需求自然生成，此时笔者引导学生自己看书理解和提炼偶函数和奇函数的定义，再结合图形实现概念的自主学习，同时了解了其特征：

（1）偶函数的图像关于y轴对称；奇函数的图像关于坐标原点对称.（2）奇偶函数的定义域一定关于原点对称.

对概念有了一定的了解，笔者将例题分为两组引导学生对函数的奇偶性进行辨析.

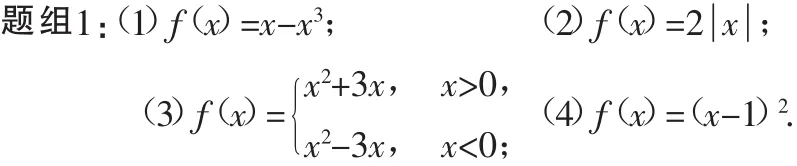
学生借助题组1的解决，对奇偶性定义进行加深理解，并初步涉及判定方法，笔者结合学生具体的解答实际，予以方法上的规范.在掌握方法的基础上，笔者进一步加大难度进行探究.

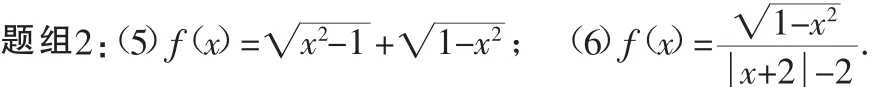
学生借助题组2这两道提高题的探究，在定义及判定方法上进一步加深理解，同时领会定义域的重要性.

在经历了两个题组的思考后，函数的奇偶性分类也自然形成，存在以下四个类型：偶函数、奇函数、既奇又偶函数和非奇非偶函数.

三、“课堂反馈”——概念应用自主化

数学概念具有系统性，在某一节概念课的教学中，学生认识和形成概念后，概念还是孤立的，未能融入整个知识体系中，记忆难以稳固，为此，要彻底地理解和掌握概念并内化为学生的能力，需要通过一定的小型综合题来应用概念.

以上述的“函数的奇偶性”一节课教学为例，笔者在最后设置了2道小型的综合题，引导学生在前后知识背景下，自主应用概念，并反馈所学.

反馈题1：奇函数f（x）在（0，+∞）上为减函数，求证：f（x）在（－∞，0）上为减函数.

反馈题2：已知一偶函数，在x＞0时表达式为f（x）=x2+3x，试求在x＜0时的表达式.

反馈题的设置，不应该是课本例题或是知识点的简单重复，应该从知识的学习过程体验出发，既要避免简单练习引起的乏味感，也要避免复杂练习引起的挫败感，基于本课所学知识适当地与前期所学知识有机组合，通过多元化的拓展，让学生在自主应用过程中内化所学知识，同时在对原有概念思考的过程中获得新的感悟.当然，考虑到学生的个体差异，不可能所有的学生在应用数学概念解决问题时，都能快速地得到正确的结果，出现漏洞是正常现象，是其思维最为真实的反映，恰好可以借助做题的过程将概念理解上的偏差暴露出来，及时地发现理解上的缺陷，及时地予以弥补，有利于概念体系更好、更稳定的构建.甚至有些时候，强化学生的思维缜密性，还需要设置一些“陷阱题”，“挖坑”让学生先摔疼了，再从其错误出发，顺势进行成因的剖析，引导学生体验“从跌倒到爬起”的过程，更为全面的理解概念和方法.

总之，高中数学教学中最为重要的一环为概念教学，概念是整个高中数学体系的枢纽，概念教学难也是不争的事实，传统的教学模式下学生很快地能够记住概念，不过对概念的理解难以深入，由于学习缺乏自主性，某一个概念学习的经验很难迁移应用到其他数学概念的学习中去，导致概念学习连贯性的缺失，链式反应下，学生的数学素养和解决数学问题的能力得不到很好的提升，所以，我们从新课程本身教学的理念出发，注重学生课堂学习的参与度，通过学生的自主探究，吸取概念中的“营养”，提升数学素养.

1.李启柱.数学建构主义学习及主要特征［J］.数学通讯，2000（5）：10.

2.郭桂华，刘新春.培养数学能力的三个重要环节［J］.中学数学月刊，2008（2）.