浅谈数学解题中常见的思想方法

☉湖北省浠水县实验中学 饶金华

中考试题涉及众多知识点，覆盖面广，关系复杂，证法灵活，解决这类考题需要考生能够正确地综合运用数学解题思想和方法，以下是中考中几种常用的解题思想，供大家参考.

一、整体思想

注意力和着眼力放在问题的整体上，通过研究问题整体形式和整体结构，进而作出整体处理，达到顺利解题的目的.

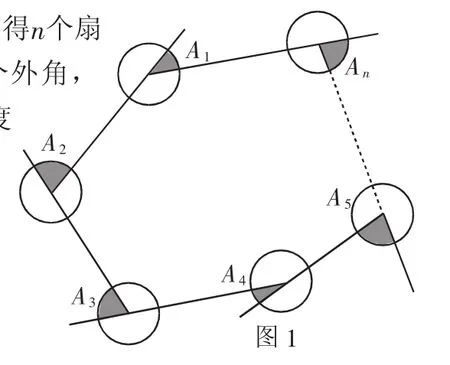
例1 如图1所示，分别以n边形的顶点为圆心，以单位1为半径画圆，则图中阴影部分的面积之和为______个平方单位.

解：由条件可知图中每个扇形的面积不能单独求出，因为不知圆心角的度数.仔细分析可得n个扇形的圆心角恰为n边形的n个因此，n个扇形的圆心角的度数和为n边形的外角和.所以阴影部分的面积之和π.

二、化归思想

化归思想是一种由陌生向熟悉转化，由未知向已知转化，又非基本问题向基本问题转化的解题策略.

例2 判断下列数3555、4444、5333的大小关系是______.

分析：直接计算每个数显然复杂难以比较，如果将它们化归为异底数同次幂的形式，然后比较底数的大小即可解决问题.

解：3555=（35）111=243111，4444=（44）111=256111，5333=（53）111=125111.

即5333＜3555＜4444.

三、分类思想

分类讨论是重要的数学思想，解答这类题不仅要求学生有扎实的基础知识，还要求学生具有灵活运用数学思想方法的能力.在对数学对象进行分类中寻求解答的一种解题思想方法.其目的在于克服思维的片面性，防止漏解.

例3 如图2，在直径为50cm的圆中，弦AB=40cm，弦CD=48cm，且AB∥CD.求AB与CD间的距离.

分析：由圆的对称性，可知两条弦的位置会出现两种情况.

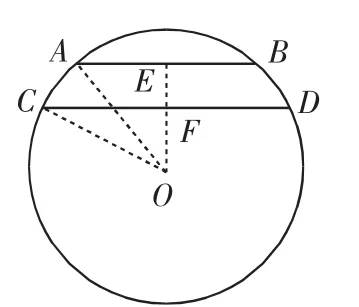
图2

图3

解：作OE⊥AB，垂足为E，OE交CD于点F.

因为AB∥CD，所以OF⊥CD.

连接OA、OC.

（1）当AB和CD位于点O的同侧时（图2），AB与CD间的距离为：

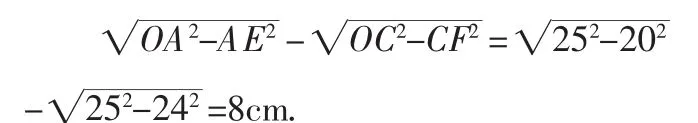
（2）当AB和CD位于点O的异侧时（图3），AB与CD间的距离为：

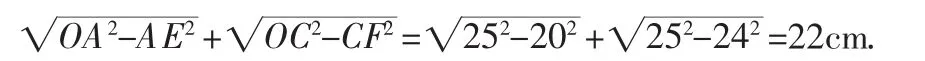
所以AB与CD间的距离是8cm或22cm.

四、数形结合思想

数形结合思想是指将数（量）与（图）形结合起来进行分析、研究、解决问题的一种思想策略.有关函数及其图像的题目，多数用数形结合思想解答.

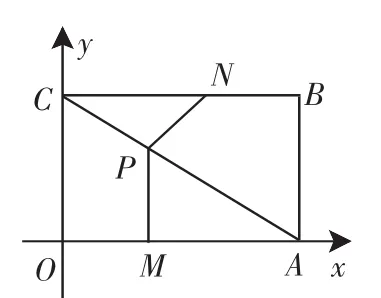
图4

例4 如图4，平面直角坐标系中，四边形OABC为矩形，点A，B的坐标分别为（4，0），（4，3），动点M，N分别从O，B同时出发.以每秒1个单位的速度运动.其中，点M沿OA向终点A运动，点N沿BC向终点C运动.过点M作MP⊥OA，交AC于P，连接NP，已知动点运动了x秒.

（1）P点的坐标为（______，______）（用含x的代数式表示）.

（2）试求△NPC面积S的表达式，并求出面积S的最大值及相应的x值.

（3）当x为何值时，△NPC是一个等腰三角形？简要说明理由.

解：（1）由题意可知C（0，3），M（x，0），N（4-x，3）.

（2）设△NPC的面积为S，在△NPC中，NC=4-x，NC边上的高为，其中0≤x≤4.

（3）如图5，延长MP交CB于Q，则有PQ⊥BC.

①若NP=CP.

③若CN=NP，则CN=4-x.

在Rt△PNQ中，PN2=NQ2+PQ2.

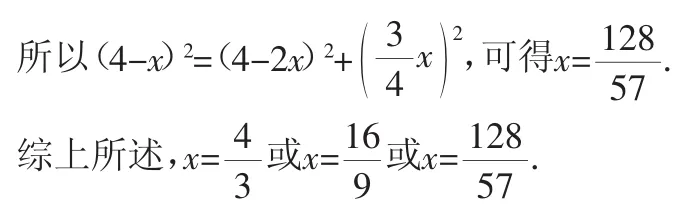
图5

小结：数学思想方法还有很多，比如方程思想，它是指对所求数学问题通过列方程（组）求解的一种解题思想，是解几何问题的重要策略.这类题目很常见，需要同学们去多观察、多动脑、多实践.