例谈运用引申技术改编初中数学试题

◎江苏省南通市北城中学 蔡新春

编制数学试题是初中数学教师的基本技能之一，独立编制原创数学试题确实费心费力，难度较高，但是我们可以借助于一些成题将其适当改编成有新意的题目.

罗增儒教授早在2005年《中等数学》上谈到用引申技术将成题改编为竞赛试题.他说：“引申通常解释为从旧义得出新义.竞赛命题的引申技术就是从已知题目出发，沿纵横两个方向演绎深化得出新题目.”本文借助一些例题浅谈如何用引申技术来改编初中数学试题.

一、不改变原题条件，在原题的结论的基础上继续向纵深研究，开发新题

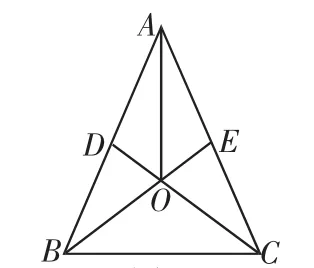
图1

例1 如图1，等腰三角形ABC中，AB=AC，D、E分别是在AB、AC的中点，BE、CD相交于点O，求证：（1）OD=OE.（2）AO平分∠BAC.

这是在学习等腰三角形时，许多老师都会让学生练习的一道题目.如果在此基础上，我们联想到三角形的中线可以将三角形分成面积相等的两个三角形，再加上△ADO与△AEO全等，那么很容易得出△ADO、△AEO、△BDO、△CEO这四个三角形的面积相等，都是△ABC面积的因此，我们可以在原题的基础上增加第（3）问：求△BOC与△ABC的面积比.

二、在原题的基础上，再适当添加条件，将问题引向深入

图2

例2 如图2，△ABC中，AB=AC，点D在AB上，点E在AC的延长线上，且BD=CE，DE与BC相交于F点，求证：DF=EF.

这是一经典老题，过点D作AC的平行线DG交BC于点G，很容易证得△CEF≌△GDF，从而得到结论.

如图3，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于点D，则DE的长为（ ）.

而湖北武汉一地区则在这题的基础上做了更深入的开发：已知△ABC是等边三角形，点P是AC上一点，PE⊥BC于点E，交AB于点F，在CB的延长线上截取BD=PA，PD交AB于点I，PA=nPC.

（3）如图6，若点P在AC边的延长线上，且n=3，其他条件不变，

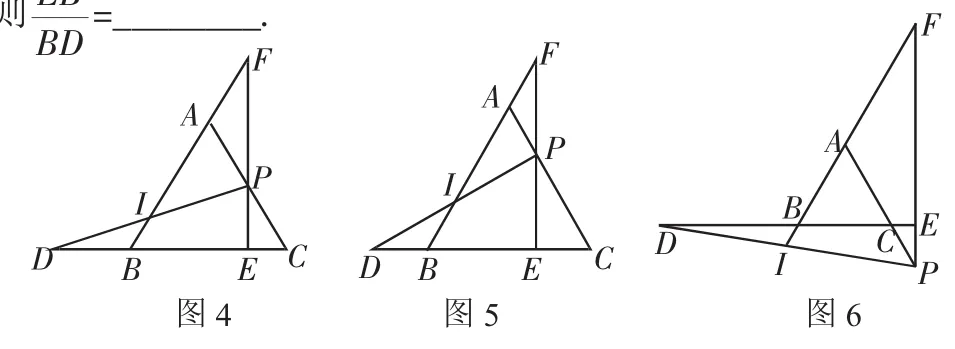
三、将原来题目中的某些条件从特殊转化为一般，进行推广开发新题

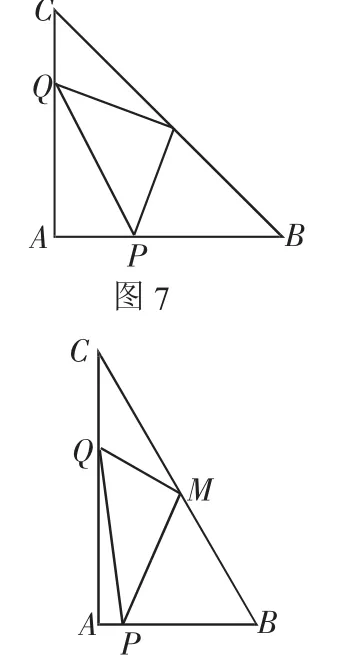
图8

例3 如图7，在Rt△ABC中，∠BAC=90°，AB=AC，M是BC边的中点，点P在线段BA上运动，同时点Q在线段AC上运动，且始终保持MQ⊥MP.试探求BP2、PQ2、CQ2三者之间的数量关系，并说明理由.

这是一道经典老题，做完后，我们进一步思考，当这个直角三角形不是等腰直角三角形而是一般直角三角形时（如图8），这个结论是否成立呢？经过研究发现，这个结论是成立的.江苏省扬州市就将按这个思路改编的题目作为2011年中考压轴题的最后一问.

四、根据解题方法的相似，改变原题背景，重新编题

例4 如图9，边长为2的正方形ABCD的对角线交于点O，另有一边长超过2的正方形的一个顶点在位于点O，并且绕点O作逆时针旋转，那么旋转过程中，两个正方形重合部分的面积是否会发生变化？如果不变，请求出它的面积.

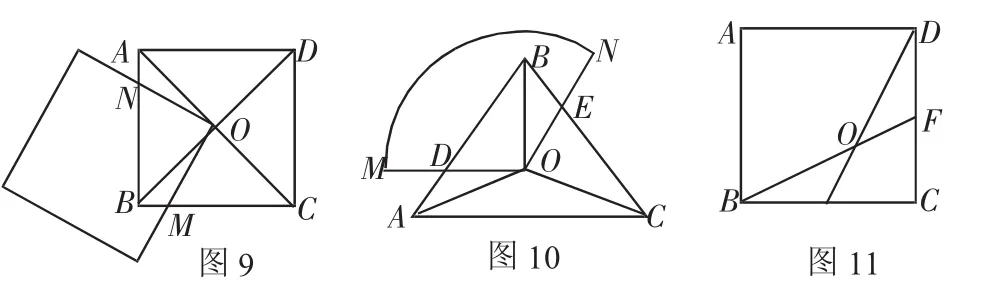
此题常用的一种解题方法是利用正方形的性质证明△AON与△BOM全等，从而得到四边形BMON的面积等于△AOB的面积.将原题中的正方形换成等边三角形后，解题的方法基本不变，因此可以改编成这样的题目：如图10，点O是等边△ABC的角平分线的交点，MON是一个扇形（OM和ON足够长）且∠MON=120°，OM、ON分别与AB、BC交于D、E两点.如果△ABC的面积为S，将扇形MON绕点O旋转时，扇形MON与△ABC重叠部分的面积是否会发生变化？如果不变，请求出它的面积.

同样利用这种方法，我们可以将例1中等腰三角形换成正方形，改编这样的新题：如图11，E、F分别是正方形ABCD的边BC、CD的中点，BF与DE相交于点O，求四边形ABOD与正方形ABCD的面积比.