几何画板在初中数学教学中的应用初探
☉江苏省苏州工业园区第六中学 毛建兴
借助几何画板辅助教学营造了一种良好的课堂氛围,使课堂教学更加形象生动,既可以充分发挥教师的主导作用,又能使学生成为学习的主体,更可以让学生借助几何画板自主进行探索学习,真正改变学生的学习方式,使学生乐意并有更多的精力投入到探索性的数学活动中去,成为数学学习的主人.下面结合自己的教学实践,谈谈几何画板辅助初中数学教学的一些粗浅做法.
一、利用几何画板增加课堂容量,提高课堂学习效率
数学课堂教学中,经常需要作函数图像、几何图形,如果以传统的教学手段,作图经常会花费许多时间,而且在教师作图的同时,部分学生注意力分散,影响学生思维,导致课堂效率低下.利用几何画板能轻而易举解决这个问题.几何画板最基本的功能之一,就是能快速准确的作出数学中的一些常见图形,而且作出的图形规范标准,有利于学生观察思考.
例1(苏科版八年级)在给出的平面坐标系中,分别写出A、B、C坐标;并在平面直角坐标系中描出下列各点的位置:D(2,4),E(-2.5,3),F(-3,-2),G(1.5,-3.5).
讲解过程中,画一张较为标准的直角坐标系图形,需要花费不少课堂时间.而借助几何画板中的“绘图/定义坐标系”功能,快速清晰的把直角坐标系呈现给学生,节省了许多课堂时间.同时,利用“画点”工具,非常方便的在坐标系内增加一些点,让更多的学生来参与抢答,有效的拓展课堂容量.为了体现“点和有序实数对一一对应”,可以先请一位学生说出点的坐标,再请另一位学生在屏幕上找出该点的确切位置.教学过程中,借助几何画板扩充了课堂教学容量的同时,也给学生创造了更多的展示机会.
另外,在备课过程中,如果能巧妙地利用几何画板中“设置超链接”、“增加页”等功能,将事先需要的内容分类准备好,那么在有限的课堂教学时间内,必将进一步加快课堂进程,加大课堂容量,更好地提高课堂效率,达到教学目标.
二、利用几何画板创设情境,提高学生的学习兴趣
新课程理念强调让学生在一定的情境中学习,数学课堂教学中熟练而恰当地创设各种情境,能够激发学生浓厚的学习兴趣,提高教学效率,使学生更容易理解、掌握数学知识.几何画板具有可操作性,能方便、清晰、准确地创设多种数学情境.利用几何画板构造动态的几何图形,来调动学生学习兴趣和探究热情,引导学生积极参与课堂教学.
例2(苏科版八年级)教学“§2.1勾股定理”设计情境导入,利用几何画板中的“变换/深度迭代”功能,构造出奇妙美丽的“勾股树”,颜色和数目可以随着图形的运动而不断改变,给人一种赏心悦目的感觉,让学生欣赏数学的美,激发学生好奇心.当将参数化为1时,图形就简化为本课的研究对象,唤起学生的求知欲(如图1).
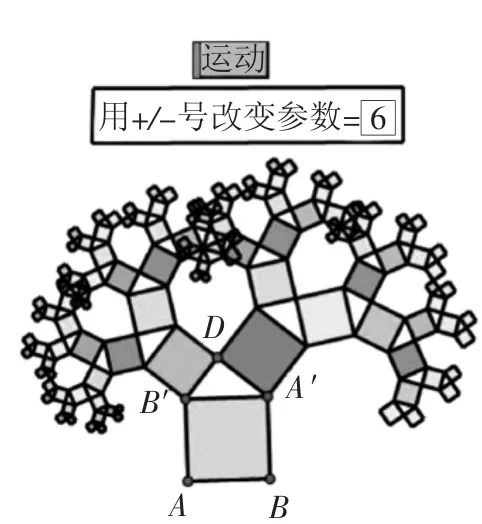
图1
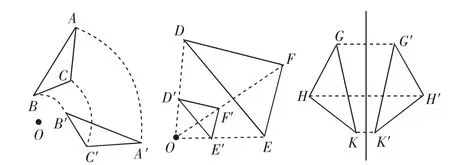
图2
苏科版中“图形与图形的变换”教学,借助几何画板菜单“变换/旋转、缩放、反射”,可以方便设计出很多优美的旋转图形、位似图形、轴对称图形,让学生感悟数学的美.同时,借助几何画板,可以为学生创设实验情境,在教师的引导下,很容易激发学生的探究热情(如图2).
三、利用几何画板进行课堂教学演示,突破教学重点和难点
初中数学中,许多数学概念和性质,具有高度的概括性和抽象性,学生难以理解、不容易接受,而这部分知识往往又是教学的重点.数学家华罗庚说过:“数缺形时少直觉,形缺数时难入微”,“数形结合”是突破教学难点、重点的有效途径,借助几何画板将抽象内容具体化,用鲜明形象的直观教学手段,把静态的图形动态化的演示,强化学生的感知.几何画板的演示过程,符合学生的认知规律和心理特征,配合教师的辅助讲解,能帮助学生理解概念,促进学生对知识的掌握,顺利化解教学中的重点、难点.
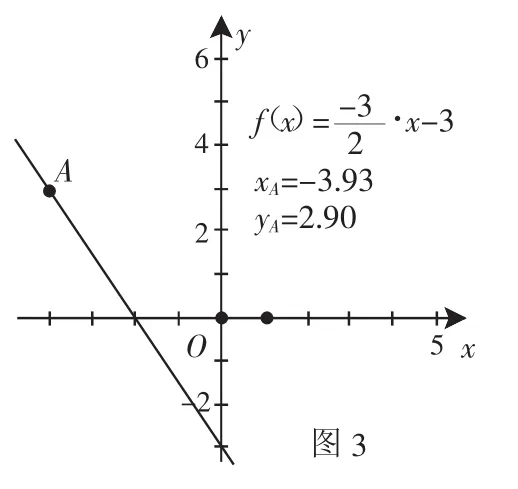
例3(苏科版八年级)观察一次函数的图像,找出函数图像的变化规律.对于初二的学生来说,文字表述“y随x的增大而减小”很抽象,学生往往靠死记硬背来“掌握”,而非真正明白它所表述的含义.为了加深对这句话的理解,利用几何画板中“绘图/绘制新函数”先作出的图像,利用菜单“构造对象上的点”在直线上取一个A,然后分别度量出A点的横坐标xA、纵坐标yA,在直线上拖动点A,让学生观察xA、yA的大小变化,随着点A的移动,学生很轻松的就能找到了变化规律,对“y随x的增大而减小”的理解水到渠成(如图3).
y=-3x-3 2
同样地,一次函数y=kx+b中参数k、b含义,是教学的重点,对好多学生来说也是难点.如果借助几何画板把k、b动态的展现给学生,突破这个难点是很容易的.操作过程中随着教师不断按“+”或“-”号,来控制参数k、b的变化,直线图像在几何画板上的变化就动态的展现出来,加深了学生对知识的理解(如图4).
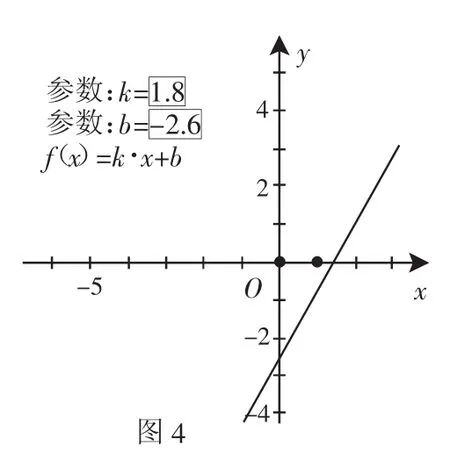
四、利用几何画板引导学生探究学习,实现自主构建知识
《数学课程标准》指出:“除接受学习外,动手实践、自主探索与合作交流也是数学学习的重要方式.”传统教学中学生一般是从教师那里被动接受事实,而几何画板给学生提供了更多动手的机会,为数学探究提供了有效的手段,使学生由“听数学”转为“做数学”,真正成为学习的主体.利用几何画板“做数学”,学生通过主动地探索,经历实验、观察、猜想等活动过程,感知知识的形成过程,变被动的接受知识为主动的探究构建知识,完全符合建构主义理论的核心思想.近几年来,学校开展小组合作学习,发现在小组合作学习模式,学生利用几何画板探究数学活动是相当有效果的.
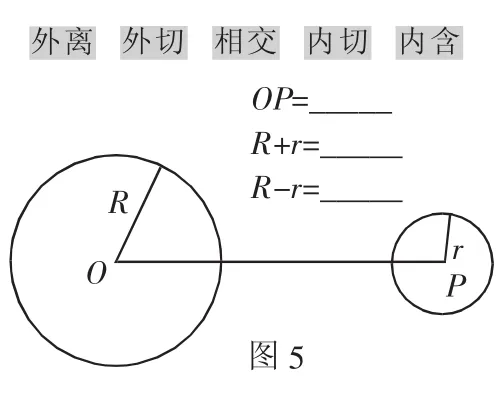
例4(苏科版九年级)“§5.6圆与圆的位置关系”,学生已经学习了“直线和圆的位置关系”,具备了一定的经验基础.教学中,利用几何画板中图形移动度量值随之动态改变的特性,给学生足够的时间,引导学生自主探索,为更好引导学生进行“两圆位置关系”的探究,设计几个问题加以恰当引导:
①几何画板中如何画一个圆心可以移动,但半径不能改变的圆?
②在操作圆移动过程中,请注意观察两圆的公共点变化情况?③如何定量判断两圆的位置?
④仿照已经学过的“直线和圆的位置关系”,你认为选取什么的量来作为判断的依据较恰当?
⑤你所找到的两圆不同位置关系中,哪几种有共同点?
⑥按照不同的标准,两圆的位置关系可以分成几类?你的依据标准是什么?
借助几何画板,学生上台展示探究过程.让学生自己归纳出:圆的移动变化产生五种不同位置,强化知识内在联系(如图5).借助几何画板,做到把教堂还给学生,通过“做数学”去获得一种体验,去改变学生的学习方式,培养了学生的探究能力.
五、利用几何画板启迪学生思维,开阔学生解题思路
几何画板是一个动态研究数学问题的有力工具,可以在变化的图形中,研究不变的几何规律.几何画板的这一特性,对启迪学生的思维能力,开发学生智力有着不可忽视的作用.近几年来,动态问题是中考的热点问题,解答时要用运动和变化的思路来审视问题,认清变化过程中的不变规律,由于涉及的信息面大,综合性强,也导致学生解答时困难重重,在平时的教学过程中,可以利用几何画板来探求未知的结论,利用几何画板中标准的图形,通过数形结合,开阔解题思路,逐步提高自己的解题能力.
例5(2005年南京中考)如图6,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中 ,∠ACB=90°,∠ABC=30°,BC=12cm. 半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
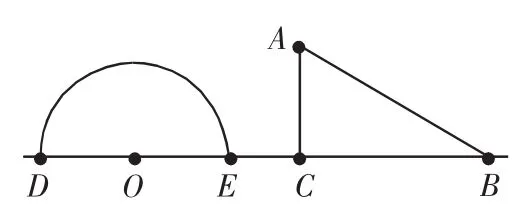
图6
(1)当t为何值时,△ABC的一边所在直线与半圆O所在的圆相切?
(2)当△ABC的一边所在直线与半圆O所在的圆相切时,如果半圆O与直线DE围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
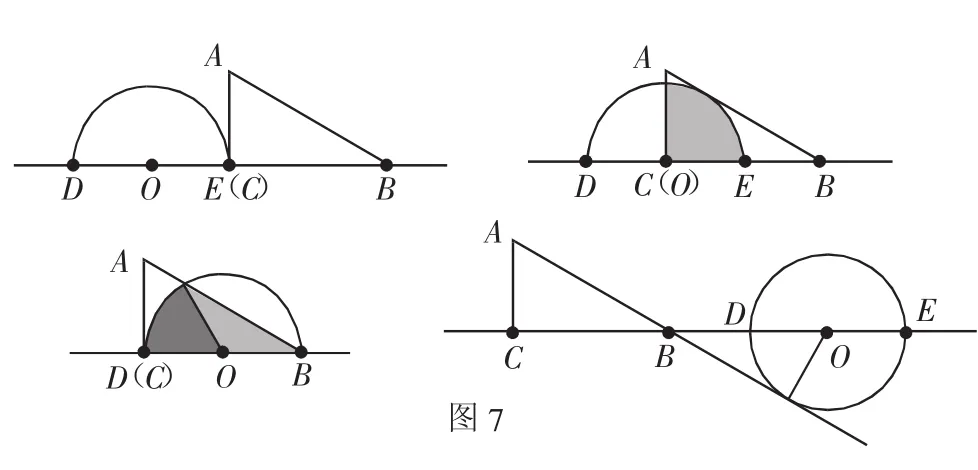
本题是圆在直线上的运动问题,解题的关键是找到所有不同的特殊位置,画出各种情况下的图形,学生往往不能准确画图,存在漏解.在分析时,可以借助几何画板,拖动点O向右运动,让学生随着运动变化的过程,思索会出现哪种情况,这对提高学生的思维能力帮助很大(如图7).解答此类综合题型,借助几何画板探究图形运动,有助于学生通过观察变化中数据的特征,把握其中的规律,从而理解题目的内涵,提升学生的解题能力.
以上是笔者通过自己在使用苏科版的教学过程中,针对几何画板辅助数学教学,谈了一些粗浅的做法和想法.在初中数学教学中,几何画板的应用远不止这些,能利用几何画板的教学内容还有许多,需要教师不断探索,针对不同的教学内容,有选择性的应用.在提倡素质教育的今天,几何画板在初中数学中的应用将越来越广,必将打破传统的教学模式,为教改及创新的教学模式注入活力.
1.教育部.基础教育改革纲要(试行).北京师范大学出版社,2001.
2.中华人民共和国教育部.各学科《课程标准》(实验稿).北京师范大学出版社,2001,7.
3.陶维林.几何画板实用范例教程.清华大学出版社,2001.
4.忻重义,万福永.几何画板在数学教学中的应用.华东师范大学出版社,2001.
5.苏州市教育科学研究院.新课程初中学习能力自测丛书数学.上海科学技术出版社,2011.

