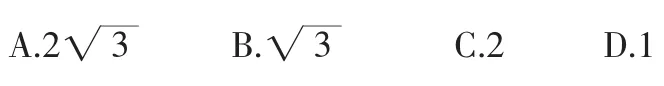中考数学思想方法总结

☉云南省红河州弥勒县西山民族中学 杨 凤

中考第二轮复习以专题复习为主线，使学生在系统掌握基础知识和基本技能的基础上形成基本的数学思想方法，使之达到系统化、结构化、完整化，进而掌握通性、通法，进一步提高学生分析问题和解决问题的能力.数学思想比较丰富，初中常见的数学思想有五大类：函数的思想、方程的思想、数形结合的思想、分类讨论的思想和转化的思想.思想是数学的灵魂，是对数学内容的本质认识，方法是思想的体现，有什么样的思想就有什么样的方法，由于思想和方法的高度统一，有时称为“数学思想方法”.下面通过分析和探究部分中考题的解法，对中考数学蕴含的思想方法作五个方面的总结.

一、函数的思想

函数的思想是用运动变化的观点分析问题和研究数量关系，也是用已知函数模型的图像和性质去分析问题、转化问题和解决问题.

例1 （2011年山东济宁市）如图1，是张老师出门散步时离家的距离y与时间x之间的函数关系的图像.若用黑点表示张老师家的位置，则张老师散步行走的路线可能是（ ）.

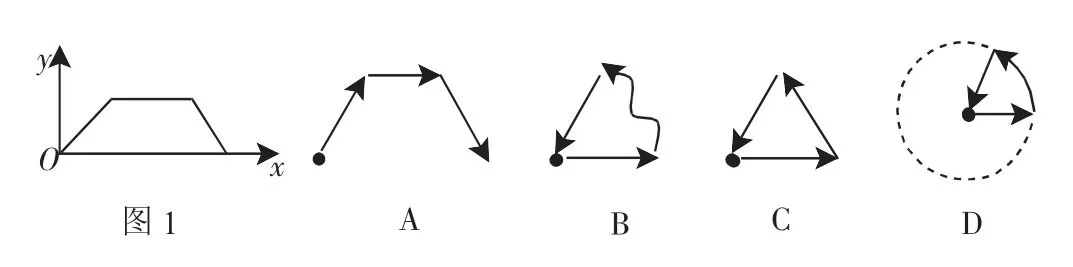
分析：图1是“距离－时间”图象，根据距离随时间的运动变化来想象和确定行走路径.

解析：由图1知道，最终距离为0，说明行走后回到出发点，有一段路程随时间的变化而不变，说明行走在圆弧上.故选D.

点评：本题着重考查看图识图能力，首先要弄清楚是什么关系图，其次要根据图象进行分析和对应的想象.

例2（2011年四川南充市）小明乘车从南充到成都，行车的平均速度y（km/h）和行车时间x（h）之间的函数图像是（ ）.

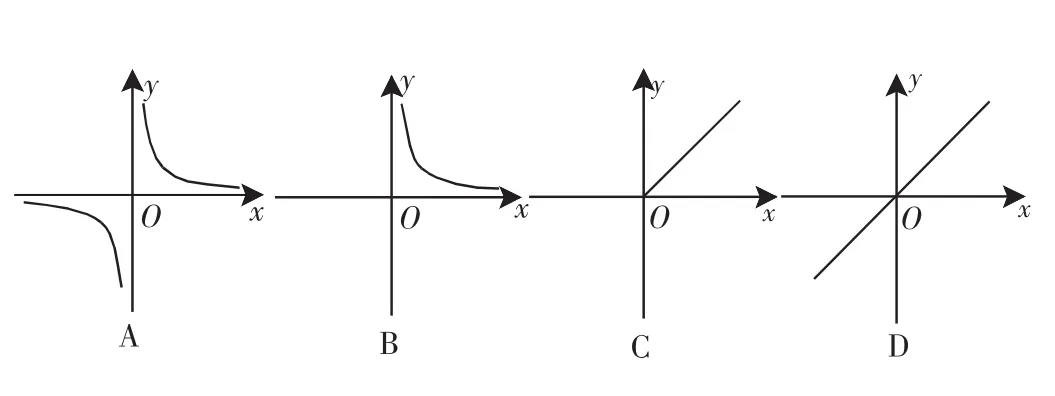
分析：根据已知条件建立函数关系，再根据函数模型确立函数图像.

解析：设南充到成都的距离是Skm，则行车的平均速度y（km/h）和行车时间x（h）之间的函数关系是因为S>0，所以由反比例函数图象知道选B.

点评：本题以实际行程为背景考查反比例函数的图像，需要能够根据实际问题建立函数关系，并运用函数模型解决问题.

二、方程的思想

方程的思想是从问题的数量关系入手，运用数学语言将问题中的条件转化为方程（组），通过解方程（组）使问题得到解决.

例3（2011年云南玉溪市）2006年我市在全国率先成为大面积实施“三免一补”的州市.据悉，2010年我市筹措农村义务教育经费与“三免一补”专项资金3.6亿元（由中央、省、市、县（区））四级共同投入，其中，中央投入的资金约2.98亿元，市级投入的资金分别是县（区）级、省级投入资金的1.5倍、18倍），且2010年此项资金比2009年增加1.69亿元.

（1）2009年我市筹措农村义务教育经费与“三免一补”专项资金多少亿元？

（2）2010年省、市、县（区）各级投入的农村义务教育经费与“三免一补”专项资金各多少亿元？

（3）如果按2009-2010年筹措此项资金的年平均增长率计算，预计2011年，我市大约需要筹措农村义务教育经费与“三免一补”专项资金多少亿元（结果保留一位小数）？

分析：（1）根据“2010年此项资金比2009年增加1.69亿元”可以列式求解；（2）根据“三免一补”的资金投入总和可以列出方程；（3）根据年增长率的计算公式：，求出下一年的专项资金.

解析：（1）2009年我市筹措农村义务教育经费与“三免一补”专项资金是3.6－1.69=1.91（亿元）.

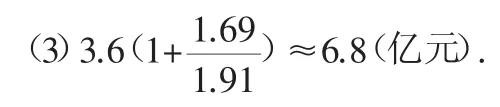
答：（1）2009年我市筹措农村义务教育经费与“三免一补”专项资金1.91亿元；（2）省、市、县（区）分别投入资金为0.02亿元、0.36亿元、0.24亿元；（3）预计2011年我市约筹措专项资金6.8亿元.

点评：解决该问题需要通过阅读发现等量关系，并找出数量之间的相互关系，如市级投资是县级的1.5倍，市级投资是省级的18倍，即县级投资和省级投资是以市级投资为连接点，若设市级投资为x亿元，则县级投资为亿元，省级投资为亿元.根据已知条件中的总投资关系建立起等量关系，从而问题得到解决.

例4（2011年湖南常德市）某城市规定：出租车起步价允许行驶的最远路程为3千米，超过3千米的部分按每千米另收费.甲说：“我乘这种出租车走了11千米，付了17元”；乙说：“我乘这种出租车走了23千米，付了35元”.请你算一算这种出租车的起步价是多少元？以及超过3千米后，每千米的车费是多少元？

分析：甲和乙说的两句话就是两个等量关系，根据这两个等量关系建立方程，问题便迎刃而解.

解析：设这种出租车的起步价是x元，超过3千米后每千米收费y元，根据题意得：

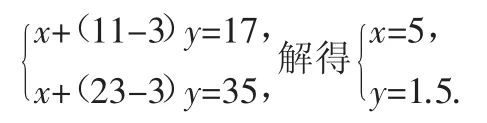
答：这种出租车的起步价是5元，超过3千米后每千米收费1.5元.

点评：这个问题涉及起步价和超过价，需要弄清楚它们之间的关系，并把已知的等量关系转化为数学符号建立方程.

三、数形结合的思想

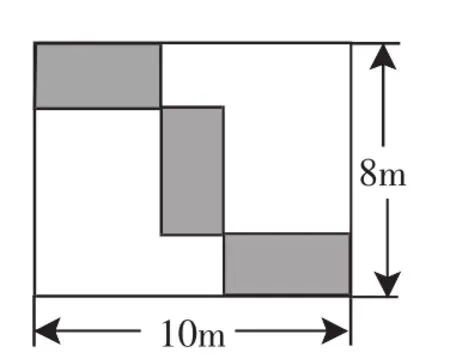
图2

数形结合的思想是在数和形之间建构一座桥梁，形成一一对应关系，既分析数量关系，也揭示几何意义，化抽象为具体，“以形助数”，“以数解形”，代数问题几何化，几何问题代数化，从而看透问题的本质.华罗庚说过：数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休.

例5 （2011年吉林长春市）在长为10m、宽为8m的矩形空地中，沿平行于各边的方向分割出三个全等的小矩形花圃，其示意图如图2所示.求小矩形花圃的长和宽.

分析：由于图形中的三个矩形花圃全等，即三个矩形花圃的长和宽分别都相等，根据三个矩形花圃和大矩形的位置关系得出数量关系，即两个花圃的长与一个花圃的宽等于矩形的长，两个花圃的宽与一个花圃的长等于矩形的宽，列出方程组求解.

解析：设小矩形花圃的长为xm，宽为ym.

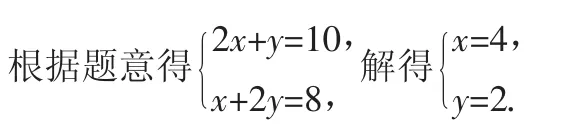
答：小矩形花圃的长为4m，宽为2m.

点评：本题以现实生活中的几何图形为背景考查图形的位置特征与数量关系，关键是“以形助数”，几何问题代数化，根据几何图形的位置特征和数量关系列出方程组，从而解决问题.

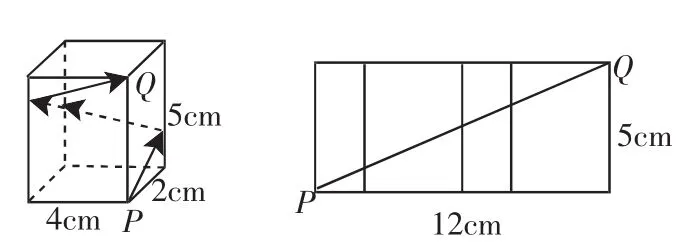
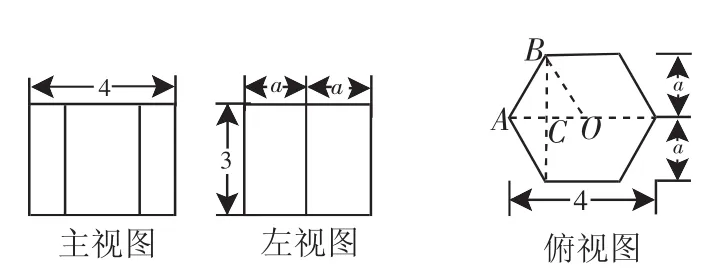
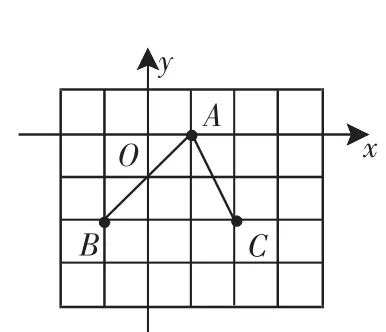
A.6

分析：先分别求出关于x的不等式的解集，再根据其他条件，结合数轴确定m的取值范围.

解析：由x－m<0得x

图3

因为不等式组的解包含4个整数，所以m的取值范围是6

点评：本题要借助数轴由数到形进行观察分析，“以形助数”使问题得到解决.

四、分类讨论的思想

分类讨论的思想是在解答某些数学问题时，有时会遇到多种情况，需要对各种情况加以分类，并逐类求解，分类讨论遵循的原则是统一标准，不重复和不遗漏.

图4

例7 （2011年江西省）在直角坐标系中，已知A（1，0）、B（－1，－2）、C（2，－2）三点坐标，如图4所示，若以A、B、C、D为顶点的四边形是平行四边形，那么点D的坐标可以是________（填序号）.

①（－2，0） ②（0，－4） ③（4，0） ④（1，－4）

分析：由于以A、B、C、D为顶点的四边形是平行四边形的位置有三种情况，故需要一一讨论确定点D的坐标.

解析：⑴以AB和BC为邻边的平行四边形时，根据图6作出点D，求得点D的坐标是（4，0）；

⑵以AB和AC为邻边的平行四边形时，根据图6作出点D，求得点D的坐标是（0，－4）；

⑶以AC和BC为邻边的平行四边形时，根据图6作出点D，求得点D的坐标是（-2，0）.故填①②③.

点评：本题以△ABC为基础的平行四边形存在三种情况，需要按位置分类解决，考虑问题要周密，否则易漏解.

五、转化的思想

转化的思想就是对一个问题等价地换一种方式、角度或观点来处理，化陌生为熟悉，化复杂为容易，化抽象为具体，化未知为已知，化实际问题为数学模型.有的数学问题只有不断地进行等价转化才能解决.

例8 （2011年湖北荆门市）如图5，长方体的底面边长分别为2cm和4cm，高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为_______cm.

图5图6

分析：由于蚂蚁爬行的路径是折线，每一条线段的长无法算出，这就需要把部分合为整体考虑，将路径展开在一个平面上作为整体考虑.

解析：将长方体沿PQ展开侧面，如图6所示.由勾股定理算得最短路程PQ是13cm，故蚂蚁爬行的最短路径长为13cm.

点评：本题考查了把部分转化为整体，用整体求路程的方法.当直接求部分行不通时，可以考虑部分构成的整体.

例9 图7是一个正六棱柱的主视图和左视图，则图中的a=（ ）.

图7图8

分析：要计算a的值就必须将数据转化到俯视图中，根据正六边形的性质进行计算.

解析：根据主视图和左视图中的数据，作出俯视图，如图8所示. 由正六边形的性质得AB=OA=2，BC=a，∠OAB=60°.在Rt△ABC中.故选B.

点评：在涉及三视图时，需要根据“长对正，宽相等，高平齐”将数据在三个视图中转化，进而进行计算，有时是几何体与视图之间进行转化.

总之，在学习数学的过程中需要不断对方法和思想进行总结，使它上升至一个高度，形成数学思想方法，并用数学思想方法指导我们解题，这样才能运用数学和驾驭数学，成为学习数学的真正主人.