运用直尺巧妙解决数学问题
☉江苏省盐城市初级中学 王太广
操作直尺(无刻度)解决数学问题,考查学生动手解决问题的能力,在充满探索的过程中理解数学,从中感受数学创造的乐趣,增进学好数学的信心,形成应用意识,创新意识.本文就运用直尺巧妙解决数学问题,举例说明.
一、平分平行四边形的面积
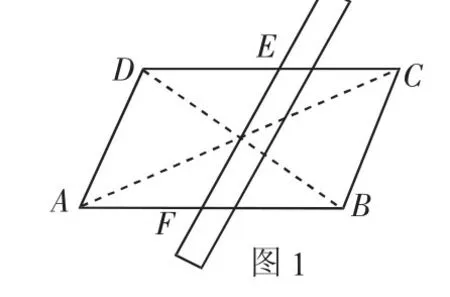
例1 如图1,已知平行四边形ABCD,只用直尺你能把这个平行四边形分成面积相等的两个图形吗?
分析:考虑到平行四边形的性质,平行四边形是中心对称图形,对称中心是四边形的对角线的交点.
作法:利用直尺连接AC,BD交于点O.过点O任意作一条直线,则直线EF两旁的图形面积相等.
根据平行四边形是中心对称图形易于证明直线两旁的图形面积相等.
二、找线段的中点
例2 在一次数学活动课上,小明提出:谁能帮我用没有刻度的直尺找出线段AB的中点?小聪说:我能做到.你知道小聪是如何做的吗?
这个问题有些困难,考查了学生的基本功和解决问题的能力.
作法:如图2,用直尺任作一条直线
MN∥AB,在MN,AB的同一侧任取一点P,连接AP,BP分别交直线MN于点C,D,再连接AD,BC,相交于点E,画射线PE交线段AB于点O,点O就是线段AB的中点.
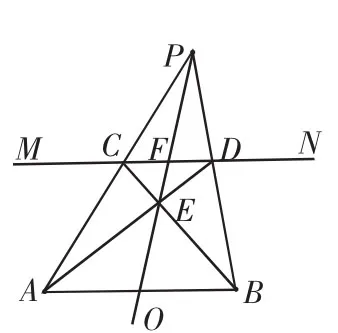
图2
三、作角的平分线
例3 只用直尺,小明画了∠BAC的平分线AD,你能知道小明如何画的吗?并证明其作法的正确性.
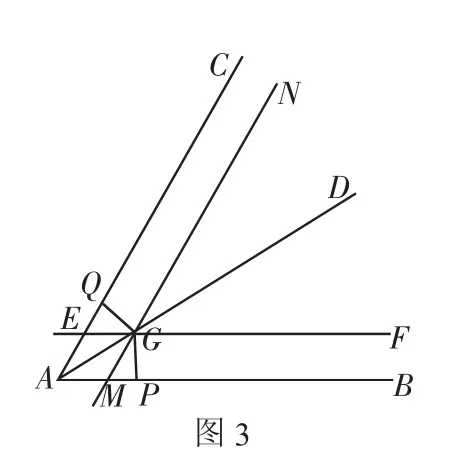
作法:如图3,将直尺一边与AB重合,在∠BAC的内部沿另一边画直线EF;再将直尺一边与AC重合,在∠BAC内部沿另一边画直线MN,交EF于点G,过AG作射线AD,则射线AD就是∠BAC的平分线.
证明:作GP⊥AB,GQ⊥AC,垂足分别为P,Q,垂线段GP,GQ为直尺的宽度,所以GP=GQ,所以AD是∠BAC的平分线.
四、作圆的直径
例4 只用没有刻度的直尺,小明能作出已知圆的直径,你知道小明是怎么做的吗?并说明理由.
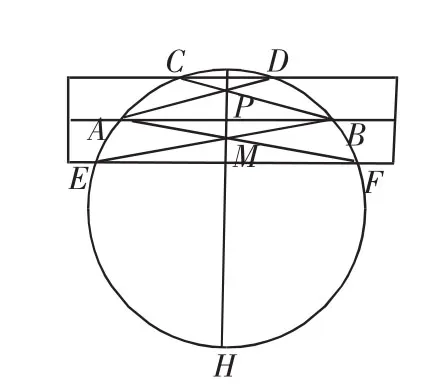
图4
作法:如图4,将直尺放在圆上,与圆交于点A,B,C,D四点,连接AD,BC交于点P,移动直尺,使直尺一边与AB重合,另一边与圆交于E,F点,(EF和CD分别在AB两侧)连接AF,BE交于点M,作直线PM交圆于G,H,则GH就是圆的直径.
证明:由作法可知,CD∥AB∥EF,AB平分∠DAF和∠CBE,从而∠DAF=∠CDE,所以四边形PAMB为菱形,PM垂直平分AB,根据垂径定理易得GH是圆的直径.
当然我们利用这种方法还可以找已知圆的圆心.
五、作垂线
例5 AB是已知圆的直径,点P是圆所在平面内的任意一点,但P点不在直线AB上,也不在圆周上,你能否仅用直尺过点P作AB的垂线?
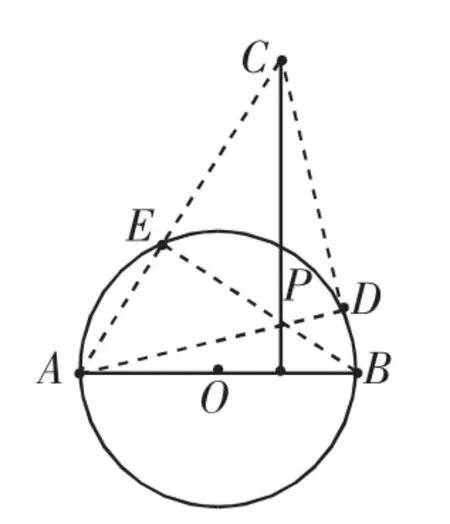
图5
分析:要作直线,还一个点,此题没有给出有关的图,也没有明确指明点P的位置,所以先要画有关的图,并就点P的位置进行分类讨论.
(1)点P在圆的内部,如图5,连接AP,BP并延长与已知圆分别交于D,E,连接
AE,BD分别延交于点C,作直线CP,则直线CP即为所求的垂线.
(2) 点P在圆的外部,有图6,图7两种情形,作直线AP,BP与已知圆分别交于点D,E,作直线AE,BD交于点C,作直线CP,则直线CP即为所求的垂线.
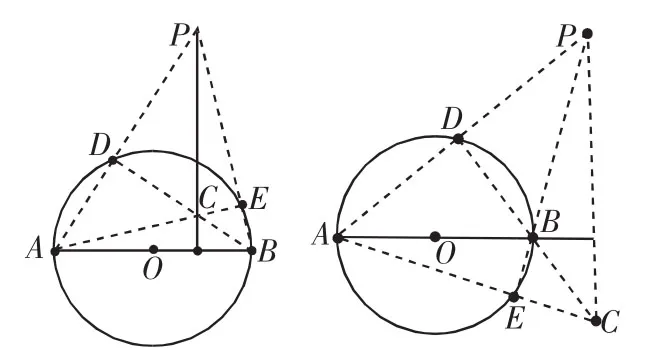
图6图7
证明:(1)点P在圆的内部,如图5,因为AB为⊙O的直径,所以AD⊥BC,BE⊥AC,所以点P是△ABC的垂心.所以CP⊥AB.
(2)点P在圆的外部的两种情况也可仿此法证明:一种情况如图6,因为AB为⊙O的直径,所以AE⊥PB,BD⊥PA.所以点C是△PAB的垂心.所以CP⊥AB.
另一种情况如图7,点B是△PAC的垂心,所以CP⊥AB.

