转化法求递推数列通项公式
☉江西省永新县禾川中学 郭海华
求递推公式数列通项公式问题,是近几年高考的热点.通常可以通过递推公式的变换,转化为等差数列或等比数列问题求解.通过变换递推关系,将非等差、等比数列转化为与等差、等比有关的数列而求得通项公式的方法称为转化法.常用的转化途径有:
一、配凑变换
将递推公式an=can-1+b(b、c是常数,且c≠1)通过配凑变成
例1 已知{an}中,a1=1,an=3an-1+2(n≥2),求an.
解:由an=3an-1+2,得an+1=3(an-1+1),则,即{a+1}是n首项为2、公比为3的等比数列.
an+1=2·3n-1,即an=2·3n-1-1.
二、倒数变换

点评:本题通过对题设中的递推公式取倒数,进而转化、构造出新的等差数列,利用等差数列的通项公式解决问题.
三、除幂变换
将递推公式an+1=can+dn(c、d为非零常数,c≠1,d≠1)除以dn+1变为
例3已知{an}中,a1=1,an=2an-1+2n(n≥2),求an.

四、对数变换
将递推公式an+1=canp(an>0,c.0,p>0,p≠1),取对数得lgan+1=plgan+lgc.

解:两边取常用对数,得lgan=2lgan-1-lga,可变为,则数列为首项、2为公比的等比数列.

五、特征方程法
若数列递推关系是an+1=pan+qan-1(p、q为非零常数),可先求二次方程x2=px+q的两根α、β,则数列{an+1+αan}是以β为公比的等比数列,从而求出原数列的通项公式.我们称这种方法为特征方程法,其中x2=px+q称为递推关系的特征方程.

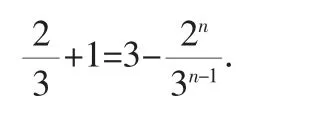
点评:特征方程法的实质是:

故数列{an+1+αan}是以β为公比的等比数列.
六、利用数列通项与前n项和的关系转化
例6 设数列{an}的前n项和为Sn,已知a1=1,Sn=4an+2.
(1)设bn=an+1-2an,证明:数列{bn}是等比数列;
(2)求数列{an}的通项公式.
解:(1)由a1=1,及Sn+1=4an+2,得a1+a2=4a1+2,a2=3a1+2=5,则b1=a1-2a1=3.

②-①得an+1=4an-4an-1,an+1-2an=2(an-2an-1).
又因bn=an+1-2an,即bn=2bn-1.故{bn}是首项为3、公比为2的等比数列.

以上六种方法是将非等差、等比数列转化为等差、等比数列的主要方法,其目的在于转化.只要我们在解题过程中灵活运用,领会其实质,那么我们在求数列通项公式问题时便会得心应手.

