浅析圆锥曲线中的配方法、待定系数法、换元法解题技巧

☉江苏省苏州大学附属中学 陆菊芳

解析几何内容是历年来高考数学试题中能够拉开成绩差距的内容之一，该部分试题往往有一定的难度和区分度，所以掌握好其中的解题方法会起到事倍功半的效果.

一、配方法、待定系数法、换元法简介

配方法、待定系数法、换元法是三种常用的数学基本方法.这些方法是数学思想的具体体现，是解决问题的手段，它不仅有明确的内涵，而且具有可操作性，有实施的步骤和作法.

二、例题解析

（1）配方法：配方法是对数学式子进行一种定向的变形技巧，由于这种配成“完全平方”的恒等变形，使问题的结构发生了转化，从中可找到已知与未知之间的联系，促成问题的解决.

例1 已知如图1所示，F1和F2为双曲线的两个焦点，点P在双曲线上且满足∠F1PF2=90°，则△F1PF2的面积是_________.

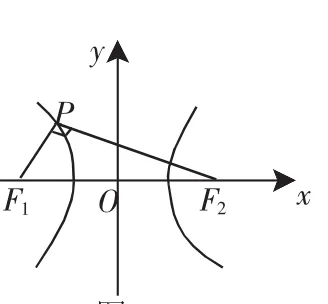
图1

评注：配方法实现了“平方和”与“和的平方”的相互转化.

（2）待定系数法：待定系数法的实质是方程的思想，这个方法是将待定的未知数与已知数统一在方程关系中，从而通过解方程（或方程组）求得未知数.

例2 设双曲线的中心是坐标原点，准线平行于x轴，离心率为，已知点P（0，5）到该双曲线上的点的最近距离是2，求双曲线方程.

二次曲线的对称轴为y=4，而函数的定义域为y≥a或y≤-a，因此，需对a≤4与a>4分类讨论.

（1）当a≤4时，如图2可知函数在y=4处取得最小值.

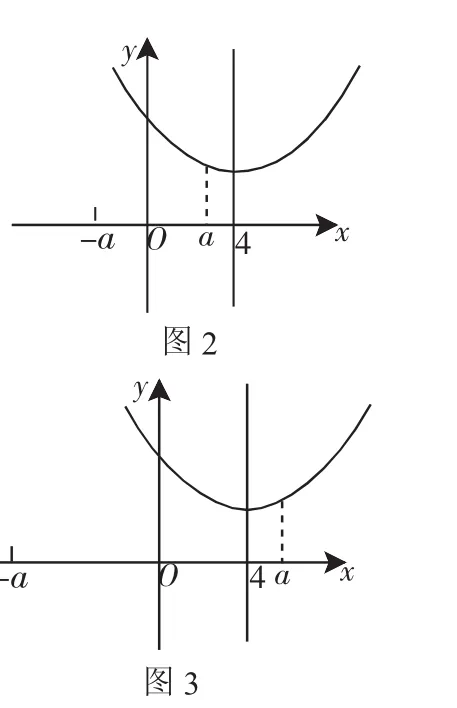
（2）当a>4时，如图3可知函数在y=a处取得最小值.

评注：此题是利用待定系数法求解双曲线方程的，其中利用配方法求解二次函数的最值问题，由于二次函数的定义域与参数a有关，因此需对字母a的取值分类讨论，从而得到两个解，同学们在解答学习题时应学会综合运用数学思想方法解题.

（3）换元法：换元法是一种变量代换，它是用一种变数形式去取代另一种变数形式，从而使问题得到简化，换元的实质是转化.

例3 如图4，已知在矩形ABCD中，C（4，4），点A在曲线x2+y2=9（x>0，y>0）上移动，且AB，BC两边始终分别平行于x轴，y轴，求使矩形ABCD的面积最小时点A的坐标.

评注：换元前后新旧变量的取值范围是不同的，这样才能防止出现不必要的错误.

故对于高考，从命题所追求的目标来看，小题所涉及的内容一定会注意到知识的覆盖，兼顾到对能力的要求.所以最近几年高考命题的热点有：

（1）与其他知识进行综合，在知识网络的交汇处设计试题（如与向量综合，与数列综合，与函数、导数及不等式综合等）；

（2）直线与圆锥曲线的位置关系，由于该部分内容体现解析几何的基本思想方法——用代数的手段研究几何问题，因此该部分内容一直是考试的热点；

（3）求轨迹方程；

（4）应用题.

因此需要同学们总结和掌握解题方法和技巧，解题时手到擒来.