求四边形未知顶点坐标例析
☉江苏省盐城市高级职业学校初中部 汪荣跃
平行四边形是初中阶段非常重要的几何图形,探求平行四边形未知顶点坐标又是近几年中考的热点话题,备受命题者的青睐.但许多学生由于不得其法而一筹莫展.现以近年来的中考试题为例,介绍一些求平行四边形未知顶点坐标的方法,供大家参考.
一、寻找相等关系,建立方程模型
例1 如图1,已知二次函数图像的顶点坐标为C(1,0),直线y=x+m与该二次函数的图像交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.
(1)求m的值及这个二次函数的关系式.
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图像交于点E,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围.
(3)D为直线AB与这个二次函数图像对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
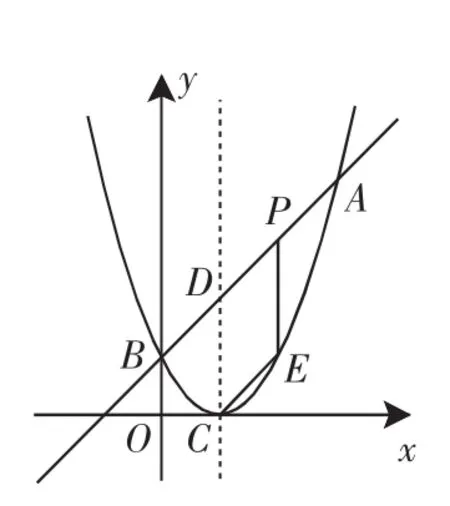
图1
解析:(1)由点 A(3,4)在直线 y=x+m上得4=3+m,则m=1.由于二次函数图像的顶点为C(1,0),因此其函数关系式可设为y=a(x-1)2,由点 A(3,4)在抛物线 y=a(x-1)2上得 4=a(3-1)2,则 a=1,所以二次函数关系式为 y=(x-1)2,即 y=x2-2x+1.
(2)设 P、E 两点的纵坐标分别为 yP和 yE,则 yP=x+1,yE=x2-2x+1,所以 PE=h=yP-yE=(x+1)-(x2-2x+1)=-x2+3x.由于点 P 是线段 AB 上的动点,因此 0<x<3.
(3)因为 PE⊥x轴,DC⊥x轴,所以 PE∥DC.因而要使四边形DCEP是平行四边形,只需PE=DC.由xD=1得yD=xD+1=2,则DC=yD=2.根据 PE=DC,PE=-x2+3x,DC=2.可得-x2+3x=2,解得 x1=1,x2=2.当x=1时,PE与DC重合,不符合要求,故舍去;当x=2时,y=x+1=3,所以满足要求的点 P 坐标为(2,3).
点评:在整个运动过程中,四边形DCEP始终保持着对边PE与DC的平行关系,但PE的长度却随着P点横坐标x的变化而变化.要使四边形DCEP是平行四边形,P点必须运动到PE=PC的特殊位置,从而为建立关于P点横坐标x的方程提供了相等关系.
二、借助平移变换,沟通坐标关系
例 2 如图 2,点 A(m,m+1)、B(m+3,m-1)都在反比例函数的图像上.
(1)求 m、k的值.
(2)如果M为x轴上一点,N为y轴上一点,以点A、B、M、N为顶点的四边形是平行四边形,试求顶点M、N的坐标及直线MN的函数表达式.
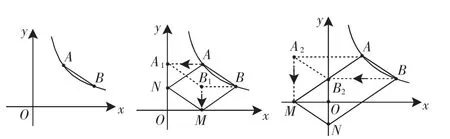
图2 图3 图4
解析:(1)由点 A(m,m+1)、B(m+3,m-1)在反比例函数 y=的图像上可得,k=m(m+1)且 k=(m+3)(m-1),从而有 m(m+1)=(m+3)(m-1),解得 m=3.所以 A、B 两点的坐标分别为(3,4)、(6,2),且 k=3×4=12.
(2)由于以点A、B、M、N为顶点的四边形是平行四边形,因此线段MN可看做由线段AB平移所得.由于点A平移后的位置可能在x轴上,也可能在y轴上,故存在两种情况:
①当点A平移后的位置在y轴上时(如图3),为了能让点A平移到y轴上,点B平移到x轴上,可以先将线段AB向左平移3个单位,到达线段A1B1位置,再向下平移2个单位,到达线段 NM 位置,此时 N 点坐标为(3-3,4-2),即 N(0,2);M 点坐标为(6-3,2-2),即 M(3,0).设直线 MN 的函数表达式为 y=k1x+b1,由 M(3,0)、N(0,2)在直线 y=k1x+b1上,得,解得所以直线MN的函数表达式为
②当点A平移后的位置在x轴上时(如图4),为了能让点B平移到y轴上,点A平移到x轴上,可以先将线段AB向左平移6个单位,到达线段A2B2位置,再向下平移4个单位,到达线段 MN 位置,此时 M 点坐标为(3-6,4-4),即 M(-3,0);N 点坐标为(6-6,2-4),即 N(0,-2).设直线 MN 的函数表达式为 y=k2x+b2,由 M(-3,0)、N(0,-2)在直线 y=k2x+b2上,得解得
点评:由于平行四边形对边平行且相等,因此可借助平移变换,沟通平移前后对应点坐标之间的关系.
三、构造全等图形,探求线段关系
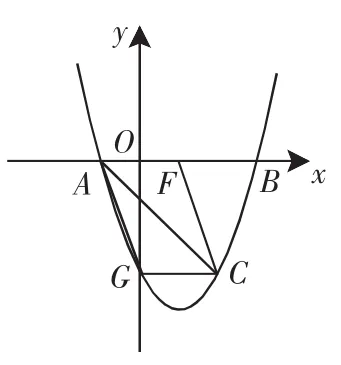
图5
例3 如图5,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式.
(2)点G是抛物线上的动点,在x轴
上是否存在点F,使A、C、F、G为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
解析:(1)把 y=0 代入 y=x2-2x-3,得 x2-2x-3=0,解得 x1=-1,x2=3,所以 A、B 两点坐标分别为(-1,0)、(3,0).把 x=2 代入 y=x2-2x-3,得 y=-3,所以 C 点坐标为(2,-3).由 A、C 两点坐标易求得直线AC的函数表达式为y=-x-1.
(2)在以A、C、F、G为顶点的平行四边形中,已经确定的线段AC可能是平行四边形的对角线;也可能是平行四边形的边,此时AC对边GF可能在直线AC上方,也可能在直线AC下方.所以本题可分三种情形讨论.
①若AC是平行四边形的对角线(如图5).此时AF∥CG,则yG=yC=-3.把 y=-3 代入 y=x2-2x-3,得 x2-2x-3=-3,解得 x1=0,x2=2,所以点 G 的坐标为(0,-3).又因为 AG∥FC,所以线段 CF 可看做线段GA向右平移2个单位所得.从而由点A的坐标(-1,0)可得点 F 的坐标为(-1+2,0),即 F(1,0).
②若AC是平行四边形的边,且GF在直线AC下方(如图6).此时点 G 和①中的 G 重合,即 G(0,-3),且有 AC∥FG.运用①中的方法,可得 F(-3,0).
③若AC是平行四边形的边,且GF在直线AC上方(如图7、图8).作CM⊥x轴,GN⊥x轴,垂足分别为点M、点N.由▱ACFG得 GF=CA,GF∥CA,所以∠GFA=∠CAF.又因为∠AMC=∠FNG=90°,所以△ACM≌△FGN.从而有 GN=CM=3,NF=AM=3.把y=3代入y=x2-2x-3,得x2-2x-3=3,解得由于 NF=3,点F可看做点 N向右平移3个单位所得,因而点F的坐标为或所以满足条件的点 F 的坐标为(1,0)或(-3,0)或
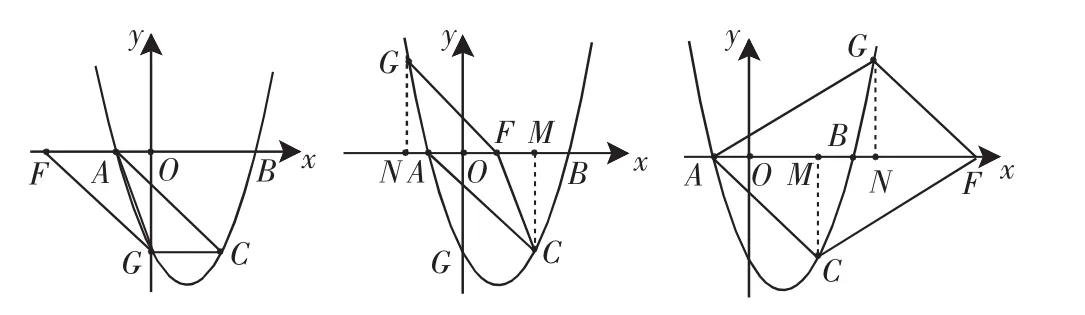
图6 图7 图8
点评:本题情形①、②中的平行四边形都有边与坐标轴垂直,借助平移变换可求出未知顶点坐标.情形③中的平行四边形的边都不与坐标轴垂直,此时可以构造两个全等的直角三角形(其斜边为平行四边形的一组对边,直角边与坐标轴垂直),进而沟通相关线段的关系.

