基于多特征参数的雷达信号调制方式识别方法

屈 直， 黄高明， 程远国， 高 敬

(1.海军工程大学电子工程学院，武汉 430033; 2.中国人民解放军92872部队，辽宁葫芦岛 125200)

0 引言

随着雷达技术的发展，雷达信号形式日趋复杂，对雷达信号的识别一直是电子对抗领域的关键技术和难点。雷达信号的脉内特性是雷达信号细微特征的重要体现，主要表现为脉内的各种调制，依据不同调制方式特点又体现在脉内信号的幅度、频率和相位上。能够用作特征提取的变换是多种多样的，但不同的变换适用于不同的处理对象。采用不同脉内调制方式的雷达辐射源脉冲信号具有不同形状的频谱，而且频谱形状的变化蕴含着脉冲信号的频率、相位和幅值的变化信息。

相像系数主要取决于两类信号的走势或者轮廓，它体现两信号的相关程度，因此相像系数可用来区分具有不同形状(或能量分布)的信号。分形维数表征信号波形的复杂度和不规则度，因此可以把雷达辐射源信号作为一种时间序列，用分形维数对其进行刻画［1－3］。分形维数是分形理论的重要参数，盒维数用以描述分形信号的复杂度，信息维数可以描述分形信号在二维平面上的分布信息。相像系数与分形维数(本文指盒维数和信息维数)对信号频谱描述是互补的，因而这两类特征能相对全面地表征信号脉内特性，便于分类识别。同时，它们具有对噪声不敏感的共同特性［4－6］，因此，在度量不同雷达脉冲信号频谱形状的变化时，运用相像系数和分形维数作为雷达信号调制方式识别的特征是可行的。另外，利用它们较好的聚类能力可以先行识别部分信号，不但提高了识别速度，而且降低分类器的设计难度与工作量。本文最后采用基于粗糙集的支持向量机(RSSVM)作为分类器。RS－SVM在小样本情况下具有良好的识别效果，可以作为一种提高小样本信号调制方式识别率的方法，与神经网络和传统的SVM相比，RS－SVM受样本数量影响小，具有更高的平均识别率和适度的训练时间及测试时间［7－9］。

1 雷达辐射源信号脉内特征提取

1.1 信号预处理

为了实现对信号特征的提取，必须对信号进行预处理。本文的预处理过程是在时域信号分离后进行的，即仅分析单一信号的谱形。预处理过程如下:

1)截获的雷达辐射源信号经采样后得到的离散信号序列为{S(i)，i=1，2，3，…，N}，N 为信号序列的长度;

2)信号序列从时域通过Fuorier变换变换到频率域，并在频率域中对信号能量进行归一化处理;

3)求出信号频谱的中心频率和有效带宽并对带宽进行归一化处理。

其中，带宽归一化处理的目的是减少特征提取的计算量、排除带外噪声的影响和扫频宽度或码长变化的影响。至此，经过预处理后得到的离散信号序列为{D(i)，i=1，2，3，…，N}。

1.2 相像系数

设有两个一维的连续正值实函数f(x)和g(x)，f(x)≥0，g(x)≥0，定义系数

式中，Crc为函数f(x)和g(x)的相像系数。算式积分的范围为函数的定义域，且函数f(x)和g(x)在其定义域内不恒为0;0≤Crc≤1;Crc相当于计算两函数的相关性，其值仅与函数的特性有关，当两函数曲线的走势差异很大时，Cr值很小，随着两函数曲线的走势逐渐趋同，Cr的值就逐渐增大，直到两函数成比例，Cr的值达到最大值。离散信号的相像系数表示为

其中:i，j=1，2，3，…，N;Cr为信号序列{D(i)}和{S2(j)}的相像系数，且{D(i)}和{S2(j)}不恒为0。对Cr的定义与Crc一致。当今雷达辐射源脉冲信号的工作频率覆盖范围很宽，一般可达0.1～40 GHz，因而在时域中提取的特征易受载频变化的影响，而在频率域中进行特征提取可消除这种影响。

由于矩形信号的能量分布很均匀，而三角形信号的能量分布比较集中，计算信号与这两种信号的相像系数可反映出这种信号的能量分布情况。先引入两个非正交的基本信号序列。

1)矩形信号序列。

2)三角形信号序列。

其中，mx是信号{D(j)}的最大值。然后将信号{D(i)}与这两种信号序列关联，提取两类相像系数。分别计算信号{D(i)}与{U(k)}和{T(k)}的相像系数，计算公式如下。

其中，k，i=1，2，3，…，N。

1.3 盒维数

分形维数是分形理论中最主要的参数，分形理论中的盒维数反映了分形信号的几何尺度。雷达辐射源信号作为一种时间序列，分形能对它进行有效的刻画［1－3］。通常用盒维数来描述分形信号的复杂程度和不规则程度，所以盒维数是雷达辐射源信号分选识别的有效特征。

用符号F(X)表示度量空间X上的全体子集组成的集类。

定义:设 A∈F(X)，(X，ρ)为一度量空间，δ＞0，用Nδ(A)表示覆盖A的直径δ的闭球的最少个数，若

存在，则称这个极限值为集A的盒维数，记为dimBA。如果集A的盒维数s=dimBA，则由式(7)可知，覆盖集A的最少闭球数服从幂定理，即对某个常数 c，Nδ(A)≈cδs。

并称A具有分形维数dimB(A)。对于数字化离散空间信号点集的盒维数有如下算式［1－2］

其中，样本间隔λ=1/fs，fs为采样率。从上面的定义可以得出盒维数只能表示分形集的复杂度，而不能反映出分形集在平面空间上的分布疏密程度，而下文中信息维数恰能做到这一点。

1.4 信息维数

实际计算可通过粗视化变换得到信息维数

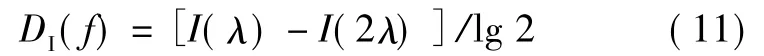
通过以上的讨论，可以获取雷达信号频谱的相像系数 Cr1、Cr2，分形维数 DB、DI，用它们组成特征向量，该向量既表征信号的整体差异程度又刻画出信号幅度、频率和相位变化的细节特征。特征向量可表示为

2 分类识别

上文所论及的方法是将接收到的信号变换为特征向量 V=［Cr1，Cr2，DB，DI］，下面的工作就是把特征向量归入到一个调制类别中。由于特征对某些调制信号有比较好的类内聚集度和类间分离度，如图1所示，因此本文先采用聚类的方法识别，这将大大降低分类器的工作量和设计的复杂度，从而提高识别效率。假设在一定的SNB范围内，有N种调制类型，通过训练估计出每种调制类型特征向量的均值Vi和协方差矩阵Mi(i=1，2，3，…，N)，(Vi，Mi)作为第 i类的重心。对待判别类型的特征向量C，它与各类的类间距离定义为

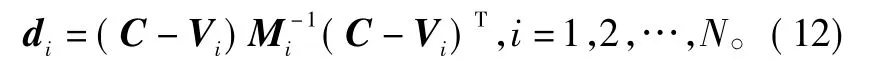
图1 信号相像系数－分形维数(DB、DI)Fig.1 Resemblance coefficient－fractal dimension(DB，DI)of four modulated signals

分类器设计是本文雷达辐射源信号识别模型的最后环节，也是雷达辐射源信号识别中的另一个关键问题。目前，人们对分类器的研究主要集中在基于神经网络和支持向量机技术的分类器。

尽管神经网络有诸多优点且在分类方面已取得长足进步，但是，神经网络在实际应用中还有许多未成功或完全解决的问题［8］。由于神经网络理论上缺乏实质性进展，促使了支持向量机(SVM)成为近年来国际上机器学习领域新的研究热点。SVM的结构如图2所示。

本文使用基于粗糙集的支持向量机(RS－SVM)分类器，本方法利用粗糙集理论在处理大数据量、消除冗余信息方面的优势，减少了SVM训练数据和处理数据的时间;同时，粗集理论的定性分析和决策能力与支持向量机的分类识别能力、容错能力和泛化能力相结合提高分类器的性能。整个识别模型如图3所示。

图3 识别算法流程图Fig.3 Flow chart of the recognition arithmetic

3 仿真试验

选择4类典型脉冲压缩雷达信号进行仿真实验，这4类信号调制方式分别为:线性调频(LFM)、非线性调频 (NLFM)、二相编码 (BPSK)、四相编码(QPSK)，用于训练的4种调制信号均由Matlab时频工具箱产生。调制信号经时频转换后，添加高斯白噪声，分别产生信噪比为 5 dB、10 dB、15 dB、20 dB、40 dB、50 dB 的信号频谱。按此方法产生40个样本，于是每一种调制信号总共有240个训练样本。

在不同信噪比下，得到训练后不同调制信号的分形维数、相像系数分布分别如图4、图5所示。综合图4可以看出，随着信噪比的增加，分形维数(盒维数、信息维数)逐渐趋于平稳，当信噪比在15～20 dB左右时，盒维数和信息维数开始逐渐接近调制信号无噪声时的真实值，可见，分形维数确实具有一定的抗噪性;由图5可知，在Cr－SNR(相像系数－信噪比)坐标中，各调制样式不仅随着信噪比的增加逐渐趋于其真实值，而且每种调制方式中Cr1和Cr2随SNR变化的趋势也相似。

图4 不同信噪比下4种信号调制方式分形维数分布Fig.4 Fractal dimension of four modulated signals under different SNR

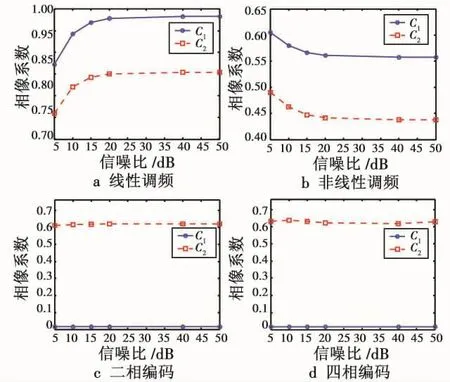
图5 不同信噪比下4种信号调制方式相像系数分布Fig.5 Resemblance coefficient of four modulated signals under different SNR

当信噪比在10～15 dB左右时，相像系数就开始接近信号无噪声时的真实值，可见，相像系数比分形维数的抗噪性更好。尤其是二相编码和四相编码的相像系数几乎不受噪声影响，如图5c、图5d所示。原因在于相像系数体现的是频谱的轮廓和形状，高斯白噪声对谱形的轮廓影响低于对分形信号谱形几何尺度和分布信息的影响。另外，从相像系数数值Cr1发现二相编码和四相编码谱形均“不像矩形”(0.017左右)，而线性调频谱形则很“像”(0.989左右)，因而利用相像系数可以很好地区分线性调频与二相/四相编码。但相像系数却不能分离二相编码和四相编码，因为它们的谱形“太像”了。

如图6所示，双相像系数坐标系中，二相编码和四相编码存在明显的交叠，无法通过聚类的手段分离。为了直观体现向量V的优越性，本文从特征向量V=［Cr1，Cr2，DB，DI］中选取 3 种代表性特征组成 V'=［Cr1，DB，DI］再次识别图5中4种调制方式的信号。如图1所示，原来交叠的信号已经明显被分开了，各调制方式的分类效果明显。说明在一定条件下，通过信号的脉内谱形特征向量 V=［Cr1，Cr2，DB，DI］识别信号调制方式是可行的。原因在于特征向量V反映了信号调制方式的内在特性。

图6 4种信号调制方式相像系数Fig.6 Resemblance coefficient of four modulated signals

当信号的调制方式可以通过特征向量V 用聚类的方法有效分离时，其结果作为最终识别结果。此步骤类似人的辨识方式，该方法对部分信号的调制方式识别可靠性高，可以作为信号分析的辅助手段，迅速归类部分信号，减少分析人员的工作强度。经过1000次Monte Carlo实验，4 种调制方式在 5 dB、10 dB、15 dB、20 dB的信噪比的平均识别率如表1所示。

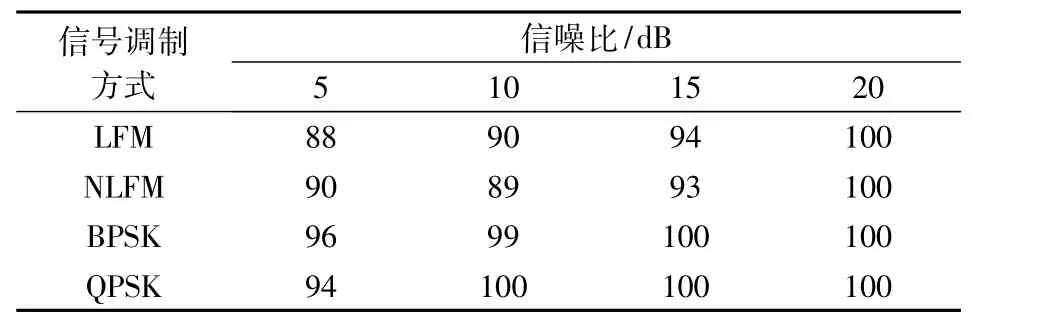
表1 基于特征向量V对信号在不同信噪比下的平均识别率Table 1 Average recognition rate based on feature vector under different SNR %

最后，运用 RS－SVM 方法［9］进行识别、印证，得到最终的识别结果。根据张葛祥对粗集、SVM、RS－SVM在辐射源识别中的研究成果［7－9，12］，本文将V作为RS－SVM 的特征向量，使用径向基核函数，径向基核函数的参数取为0.5。经过1000次Monte Carlo实验，4种调制方式在5 dB、10 dB、15 dB、20 dB的信噪比的平均识别率如表2所示。

表2 基于RS-SVM对信号在不同信噪比下的平均识别率Table 2 Average recognition rate based on RS-SVM under different SNR %

由表2可以看出在整个SNR变化范围内信号识别率都比较高，表明特征向量V的有效性，同时表明本文所提出的方法具有可行性。

4 结论

本文对雷达信号脉内调制方式的识别是在全脉冲识别后，对雷达信号更精确的辨识，这在复杂电磁环境下和脉冲压缩技术广泛应用的今天具有重要意义，也是当前研究的热点。本文从直观的谱形图中提取了反映其轮廓、复杂度及分布特性的相像系数与分形维数，利用它们良好的聚类性初选信号调制方式，而后使用基于RS－SVM分类器识别，提高识别的准确率，本方法适用于在复杂的雷达信号环境下识别雷达辐射源调制方式。通过仿真试验证明该方法的有效性，具有一定的工程应用价值。

［1］ 孙霞，吴自勤，黄畇.分形原理及应用［M］.合肥:中国科学技术大学出版社，2003.

［2］ 刘丹.实用分形图形学［M］.大连:大连海事大学出版社，2000.

［3］ 曾文曲.分形理论与分形计算机模拟［M］.修订版.沈阳:东北大学出版社，2001.

［4］ 张葛祥，胡来招，金炜东.雷达辐射源信号脉内特征分析［J］.红外与毫米波学报，2004，23(6):477－480.

［5］ 叶菲，罗景青，海磊.基于分形维数的雷达信号脉内调制方式识别［J］.计算机工程与应用，2008，44(15):155－157.

［6］ 郝研，王太勇，万剑，等.分形盒维数抗噪研究及其在故障诊断中的应用［J］.仪器仪表学报，2011，32(3):540－545.

［7］ 张葛祥.雷达辐射源信号智能识别方法研究［D］.成都:西南交通大学，2005.

［8］ 张葛祥，金炜东，胡来招.基于粗集理论的雷达辐射源信号识别［J］.西安交通大学学报，2005，39(8):871－875.

［9］ 张葛祥，荣海娜，金炜东.支持向量机在雷达辐射源信号识别中的应用［J］.西南交通大学学报，2006，41(1):25－30.

［10］ 郭双冰.基于小波和分形理论的调制信号特征提取方法研究［J］.信号处理，2005，21(3):316－318.

［11］ 吕铁军，郭双冰，肖先赐.调制信号的分形特征研究［J］.中国科学:E 辑，2001，31(6):508－513.

［12］ ZHANG G P.Neural networks for classification:A survey［J］.IEEE Trans System，Man，and Cybermeties－Part C:Application and Reviews，2000，30(4):451－462.