基于ICSM-UKF算法的UCAV目标状态估计

丁达理， 罗建军， 宋 磊， 马卫华

(1.西北工业大学航天学院，西安 710072; 2.空军工程大学航空航天工程学院，西安 710038)

0 引言

在无人作战飞机(Unmanned Combat Aerial Vehicle，UCAV)攻击目标过程中，UCAV需要对目标进行跟踪测量以获得所需的目标状态信息。UCAV目标探测与跟踪系统的测量数据一般只包含目标相对距离的粗略信息和视线角的原始信息［1］，不能直接提供目标运动的所有参数，且由于传感器测量误差、陀螺稳定器和无人机平台运动等干扰因素使得目标测量信息存在较大的噪声。目标状态估计通过对目标测量原始信息进行滤波处理，对目标运动的其他参数进行估计，得到目标位置、速度和加速度的精确估值，其精度将直接决定火控解算的精度，从而影响UCAV武器系统的武器投射命中率。

目标状态估计需要解决两个重要问题，即机动目标模型的准确建立和滤波算法的合理使用［2］。目标运动模型的建立是一个难点问题，选择合理的运动模型是精确估计目标运动状态的前提，“当前”统计模型是公认的比较切合实际的一种运动模型，并得到了广泛应用［3－6］。根据相对距离、目标视线角进行实时估计实际上是一非线性滤波问题，目前常用的非线性滤波方法有扩展卡尔曼滤波算法(EKF)、无迹卡尔曼滤波算法(UKF)和粒子滤波算法(PF)。由于EKF算法需要对模型进行线性化处理，忽略了泰勒展开的高阶项，因此会产生较大的估计误差，甚至引起滤波发散;PF算法虽然滤波精度高，但计算量大，运算时间长，所以并不适用于实时处理情况;相比二者，UKF算法具有实现较为简单、滤波精度较高、收敛性好的优点［7］。结合UCAV对地攻击的特点，综合考虑滤波算法的精度、实时性、稳定性，本文提出了一种基于改进“当前”统计模型的UKF算法(ICSM－UKF)，并仿真验证了该算法的有效性。

1 “当前”统计模型

“当前”统计模型采用修正瑞利分布描述目标加速度的统计特性［8］。所谓“当前”，是指瑞利分布函数的均值随着时间变化而变化。“当前”加速度的概率密度函数为［3－4］

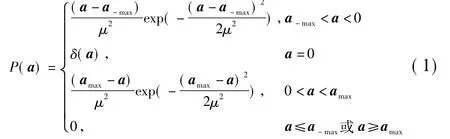
式中:amax、a－max为已知目标加速度的正上限和负下限;a为目标随机加速度;δ(·)为狄拉克δ函数，μ＞0为常数。则a的均值和方差可以表示为

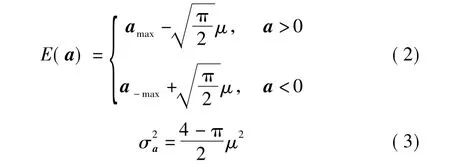
“当前”统计模型的离散状态方程为

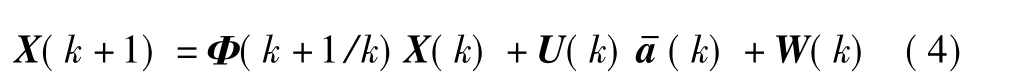
式中:X(k)=［x(k)y(k)vx(k)vy(k)ax(k)ay(k)］T，机动加速度“当前”均值是均值为零、方差为Q(k)的高斯白噪声，Φ(k+1/k)、U(k)、Q(k)分别为

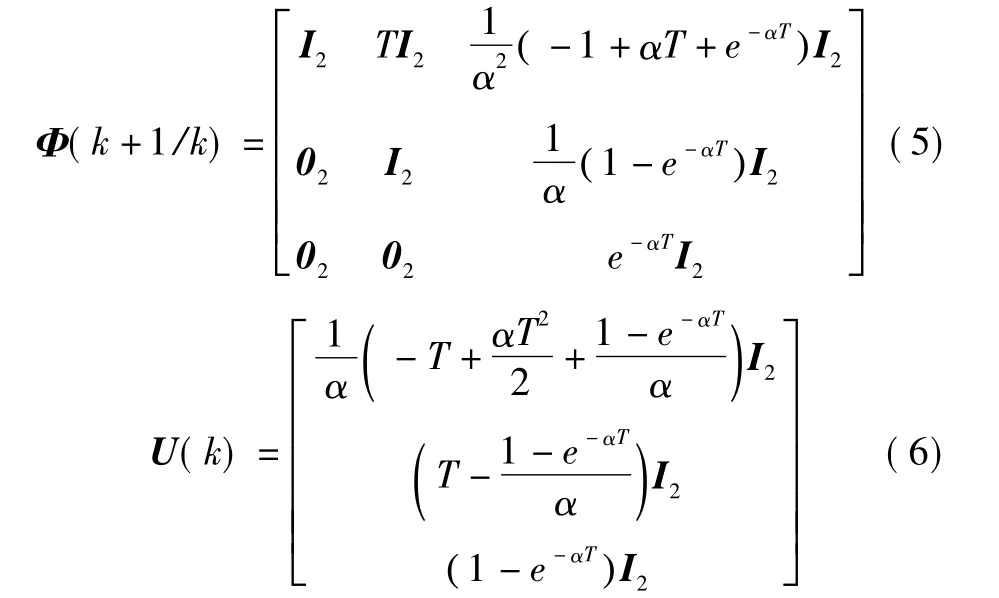
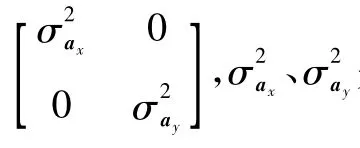
由式(2)、式(3)可得

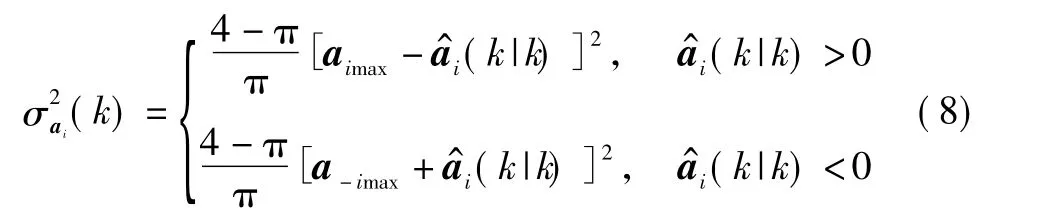
式中:i=x，y;aimax，a－imax是目标在 x、y 坐标方向所能达到的最大正负加速度值。

UCAV目标跟踪系统的量测方程为

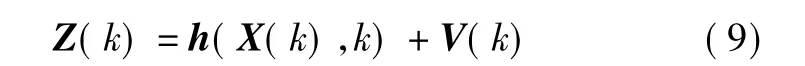
从式(8)可以看出，aimax，a－imax(i=x，y)直接影响“当前”统计模型中加速度的方差的大小又直接影响过程噪声的方差Q(k)，从而影响相应的滤波算法的性能［5－6］。

当目标的“当前”加速度为正时，由式(1)可得

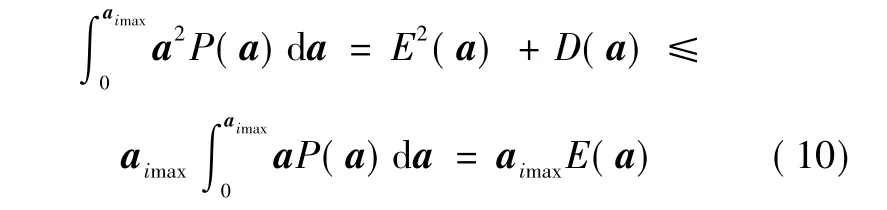
将式(1)代入式(10)可得

当目标“当前”加速度为负时，同理可得

再将式(11)、式(12)代入式(2)可得

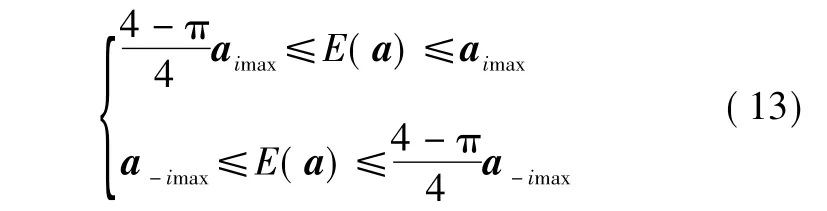
2 改进的“当前”统计模型

设加速度 ai(i=x，y)的取值范围在区间［a－p，ap］内，设定加速度阈值 a－q、aq，并使得 aq＞ ap，a－q＜ a－p，模糊隶属度函数fa为

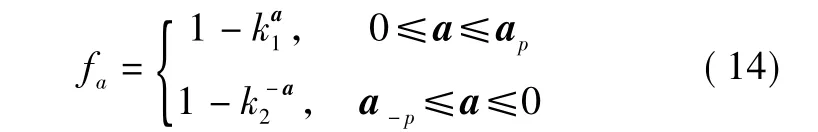
式中，k1、k2为常数，取值范围满足如下条件

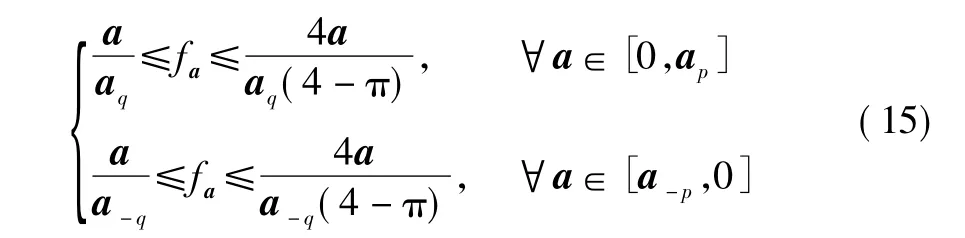
模糊隶属度函数 fa以及变量 a－q、aq、a－p、ap取值如图1所示。

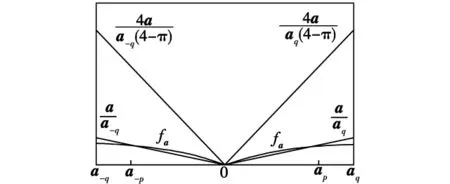
图1 非线性指数隶属度函数Fig.1 Nonlinear exponential membership function

设“当前”统计模型中的加速度上下限随着fa自适应变化，即

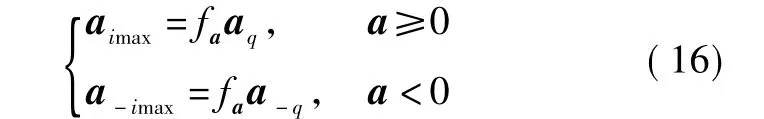
3 ICSM-UKF算法

3.1 标准UKF算法

对于非线性模型式(4)、式(9)，假设过程噪声W(k)和量测噪声V(k)为互不相关的零均值高斯白噪声，初始状态X0与所有噪声独立。UKF的基本算法步骤如下［9－10］

1)初始化，初始状态X0的先验均值和协方差阵为

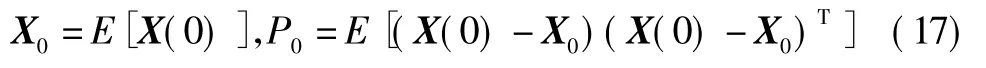
2)计算k+1时刻σ点和权系数为

3)利用状态方程传递采样点为

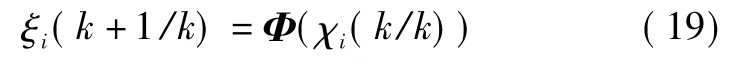
4)计算状态变量的一步预测均值和协方差为

5)利用非线性量测方程传递采样点为

6)计算量测预测值、自协方差及互协方差为

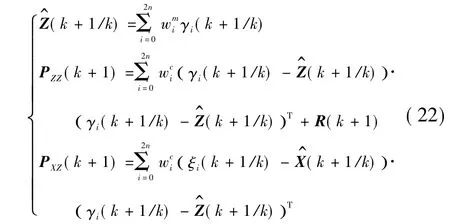
7)计算UKF增益，更新状态和协方差为式中，K(k+1)为滤波增益。

3.2 一种带量测噪声统计估计器的自适应UKF算法

与EKF类似，UKF也是以准确的数学模型和噪声统计特性已知为基础的［11］。由标准UKF算法可知，在滤波迭代过程中，它们的噪声统计特性都是先验确定的，且在整个滤波过程中是保持不变的。而在UCAV攻击目标过程中，由于目标测量与跟踪系统受陀螺稳定器、随机风、传感器分辨率、捷联惯导误差、气象环境等各种因素的影响，量测噪声的统计有时并不准确，甚至未知。而基于不变的噪声统计特性的UKF算法由于不能感知这种变化，其滤波的精度和稳定性都将受到很大的影响［12］。因此必须对标准UKF算法进行改进，使本文算法在进行滤波的同时，采用噪声统计估计器对未知或时变的噪声统计进行实时估计和修正，可提高对未知或时变噪声的适应性。下面根据极大后验(MAP)估计原理，推导出一种带次优无偏MAP常值量测噪声统计估计器的自适应UKF算法。

当量测噪声V(k)是均值不为零的高斯噪声时，假设有

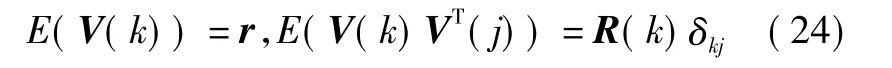
根据假设，结合文献［13］和式(9)可知最优MAP常值量测噪声统计估计器为

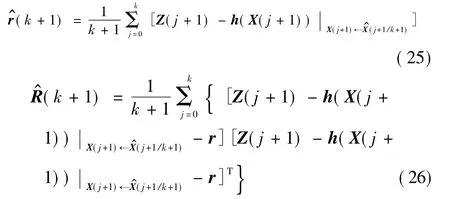
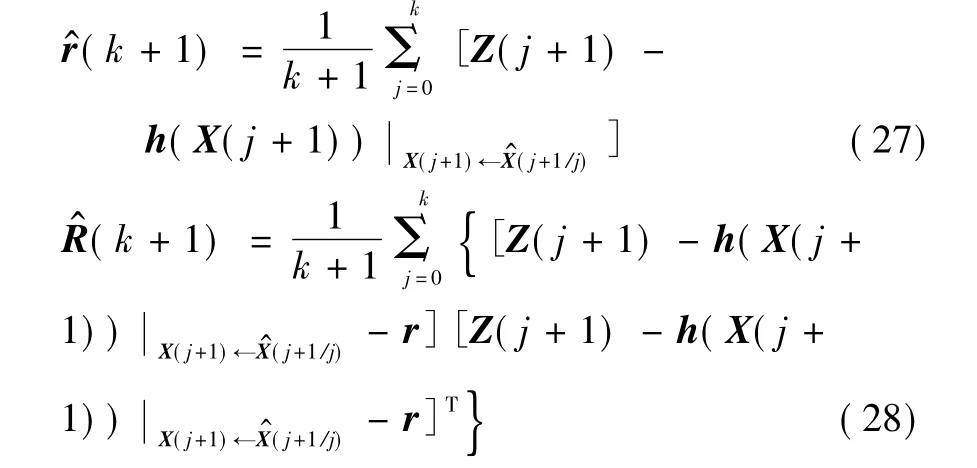
式中，χi(j+1/j)为由j+1时刻一步状态预测j)和协方差P(j+1/j)所构造的σ采样点。

将式(29)代入式(27)、式(28)，并联合一步输出预测表达式(22)，即可得到基于量测值Z(k+1)的次优MAP常值量测噪声统计估计器计算公式为

于是，可以引出次优无偏MAP常值量测噪声统计估计器为

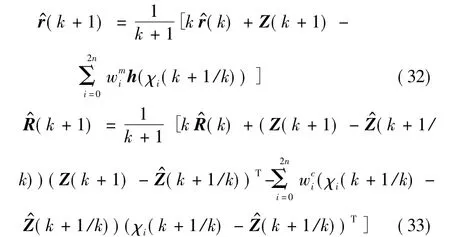
相应地，结合式(32)、式(33)，将标准UKF滤波算法中的式(21)、式(22)更新为如下形式

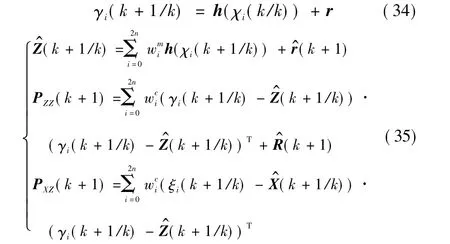
综上，式(18)～式(20)、式(23)、式(34)～式(35)是基于常值量测噪声统计估计器的自适应UKF滤波算法。

4 仿真分析

为验证ICSM－UKF算法的有效性，将其与基于“当前”统计模型的EKF算法(CSM－EKF)进行仿真对比。仿真结果的评价指标采用状态估计质量，状态估计质量取均方根误差(RMSE)，定义为

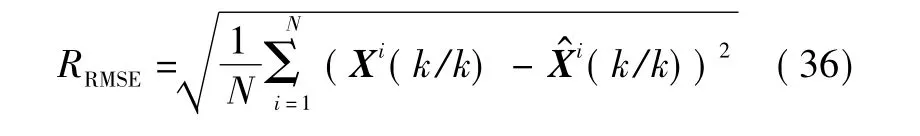
目标实际运动:假设目标初始位置为(8 km，6 km)，0 ～1 s作匀速运动，1 ～6 s以加速度(24 m/s2，18 m/s2)机动，7～14 s机动加速度变为(20 m/s2，35 m/s2)，15 ～20 s机动加速度变为(4 m/s2，8 m/s2)。目标实际运动仿真结果如图2所示。

图2 目标实际运动曲线Fig.2 Real motion curve of the target

仿真参数设置:aq=60 m/s2，a－q= －60 m/s2，ap=40 m/s2，a－p= －40 m/s2，k1=k2=0.95，α =0.1，αλ=0.01，βλ=2，κ =0;设位置初始误差均为10 m，速度初始误差为6 m/s，目标加速度误差为4 m/s2。CSM－EKF算法中参数设置为 axmax=40 m/s2，aymax=50 m/s2，a－xmax=－40 m/s2，a－ymax= －50 m/s2。

在量测噪声统计未知或不准确情况下考察ICSMUKF算法滤波精度和稳定性，并与CSM－EKF算法进行对比。采用量测噪声统计估计器对r和R进行估计，且取初始测距噪声均值为0，均方差为0.8 m;初始测角噪声均值为0，均方差为1.6 mrad。则测距和测角噪声估计值如图3～图4所示。相应地，为考察在量测噪声统计未知情况下3种算法的滤波性能，对x方向上目标速度、加速度均方根误差进行了仿真，如图5～图6所示。

从仿真图2～图3可以看出，改进的UKF算法能快速准确地估计出量测噪声的均方差，充分说明了基于常值量测噪声统计估计器的有效性。从仿真图4～图5可以看出，CSM－EKF算法在量测噪声统计未知或不准确时滤波误差较大，滤波精度低，这是因为CSMEKF算法不能自适应地调整aimax和a－imax，而且不能对未知的量测噪声进行估计，随着量测噪声的累积，误差越来越大;而ICSM－UKF算法在量测噪声统计未知情况下，不仅滤波依然收敛，而且滤波精度及稳定性具有明显优势，这与先前的理论分析相吻合。

图3 测距噪声估计值Fig.3 Estimation of range measurement noise

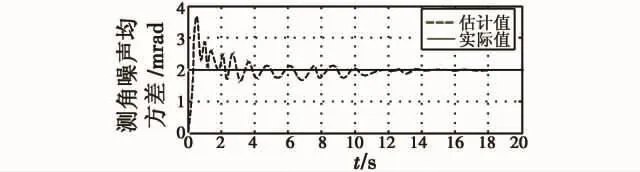
图4 测角噪声估计值Fig.4 Estimation of angle measurement noise

图5 x方向目标速度均方根误差比较Fig.5 Comparison of velocity RMSE in x direction

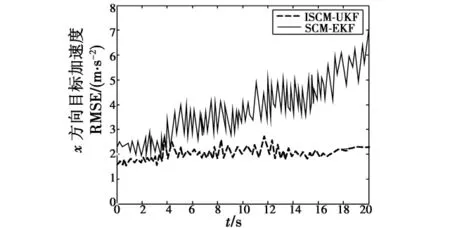
图6 x方向目标加速度均方根误差比较Fig.6 Comparison of acceleration RMSE in x direction

5 结论

本文结合UCAV目标状态估计的特点，综合考虑滤波精度、收敛速度、实时性等性能指标，提出了一种ICSM－UKF算法。该算法通过设计模糊隶属度函数来自适应调整“当前”统计模型目标加速度上下限，使其更接近目标的实际运动情况，提高了滤波精度;同时，通过设计量测噪声统计估计器对UKF算法进行了改进，使其在量测噪声统计不准确或未知的情况下，仍能保持较高的滤波精度，提高了UKF算法的抗干扰性。仿真结果表明，该算法具有滤波精度高、收敛速度快的优点，根据所设计的算法，UCAV可以快速准确地估计目标的状态参数。

［1］ 吴汉平.无人机系统导论［M］.北京:电子工业出版社，2003.

［2］ WAN E A，VAN DER MENVE R.The unscented Kalman filter for nonlinear estimation［C］//IEEE Adaptive Systems for Signal Processing，Communications，and Control Symposium，2000:153－158.

［3］ 陈勇，董永强.基于“当前”统计模型的模糊自适应滤波算法［J］.火力与指挥控制，2010，35(8):176－179.

［4］ 王炜，杨露菁.一种改进的“当前”统计模型及其自适应滤波算法［J］.系统仿真学报，2005，17(8):2037－2040.

［5］ Al DHAHER A G H，MACKESY D.Multi－sensor data fusion architecture［C］//The 3rd IEEE International Workshop on Haptic，Audio and Visual Environments and Their Applications，2004:159－163.

［6］ 王向华，覃征，杨慧杰，等.基于“当前”统计模型的模糊自适应跟踪算法［J］.系统工程与电子技术，2009，30(8):1089－1093.

［7］ 潘泉，杨峰，叶亮，等.一类非线性滤波器—UKF综述［J］.控制与决策，2005，20(5):481－489.

［8］ 周宏仁，敬忠良，王培德.机动目标跟踪［M］.北京:国防工业出版社，1991.

［9］ MERWE R V，FREITAS N D，DOUCET A，et al.The unscented particle filter［C］//Advances in Neural Information Processing Systems，1998:584－590.

［10］ WU Y X，HU D W，HU X P.Comments on performance evaluation of UKF－based nonlinear filtering［C］//Automatica，2007，43(3):567－568.

［11］ SONG Qi，HAN Jianda.An adaptive UKF algorithm for the state and parameter estimation of a mobile robot［J］.ACTA Automatica Sinica，2008，34(1):72－79.

［12］ 赵琳，王小旭，孙明，等.基于极大后验估计和指数加权的自适应UKF滤波算法［J］.自动化学报，2010，36(7):1007－1019.

［13］ 周卫东，乔相伟，吉宇人，等.基于新息和残差的自适应 UKF 算法［J］.宇航学报，2010，31(7):1798－1803.