指数分布单元组成的典型系统备件数目解析分析方法
金 星, 常 浩, 彭 博, 鲁 海
(中国人民解放军装备学院, a.激光推进及其应用国家重点实验室; b.研究生管理大队,北京 101416)
1 背景
在工程中,快速、准确地确定备件需求量对于提高系统运行可靠性有着举足轻重的作用。但在分析系统所需备件数量时,由于问题的复杂性很难求出精确解,所以一般采用蒙特卡罗仿真方法计算[1-4],但蒙特卡罗仿真计算过程十分耗费机时且计算精度不高。例如,相同指数分布单元组成的r/n系统,系统故障概率[5]为
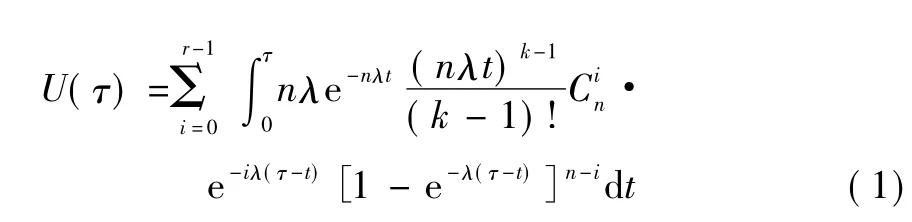
系统不可用度为
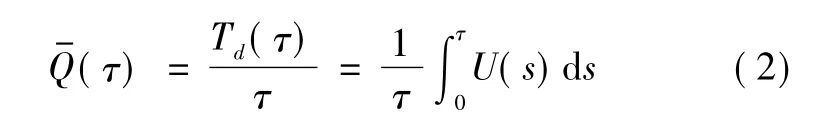
这种特殊的被积分函数以及双重积分计算,即使采用数值计算方法或蒙特卡罗仿真方法,计算过程都将是十分耗时和繁琐的。因此,工程上迫切需要一种能够快速并且准确求出备件所需数量的方法。
一般来说,相同分布单元组成的串联、并联和旁联等系统是工程中常见情况,大多数电子产品可以看成是由相同指数分布单元组成的此类典型系统。本文在假定修复时间忽略不计的条件下,采用泊松过程方法,提出系统平均可靠度的解析分析方法,由于此分析方法存在解析解,从而为工程中备件策略的制定提供了简捷并且物理意义明确的解析分析方法,具有一定的工程实用价值。
2 确定备件数目的基本方法
2.1 按照故障次数确定
设给定时间间隔(0,τ]内,产品故障次数N(τ)是随机变量,所能提供的备件数目为k,备件充足概率(不缺备件概率)p[N(τ)≤k]满足
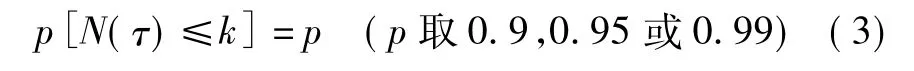
从而可解得备件数目k,备件充足概率是概率指标,工程中应用不直观、不方便[6-7]。
2.2 按照平均不能工作时间确定
设给定时间间隔(0,τ]内,所能提供的备件数目为k,要求产品平均不能工作时间满足

式中:U(t)为产品故障概率;T0为平均不能工作时间的上限值,用(0,τ]内平均不能工作时间表示,具有直观、方便的特点[8]。
2.3 按照平均不可用度确定
设给定时间间隔(0,τ]内,所能提供的备件数目为k,要求产品平均可用度满足

3 r/n系统的分析模型
为了使问题分析具有一般性,文章对n个相同分布单元组成的r/n系统进行分析,当r=1时代表并联系统情况,当r=n时代表串联系统情况。首先采用以下基本假设:1)系统由n个相同的指数分布单元组成,单元故障率为λ;2)故障单元的更换时间忽略不计,即更换时间相对工作时间小很多;3)在(0,τ]时间间隔内,所需备件数目为k。
如图1所示,在(0,τ]时间间隔内,可修复系统的故障过程分为2个阶段。
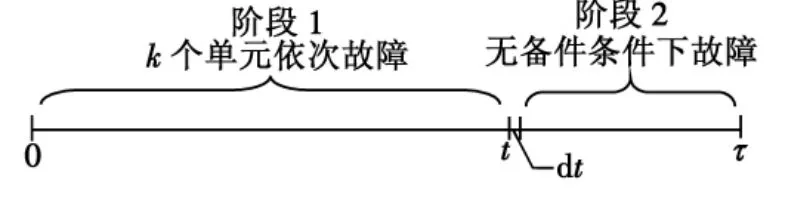
图1 可修复系统的故障过程Fig.1 The fault process of repairable system
1)阶段1:k个单元依次故障。单元发生故障次数小于或等于k,单元发生故障就有备件进行修理。在任意时刻t(t≤τ)的无限小区间dt内,n个单元中任意一个故障的故障率为nλ,根据泊松过程方法[10],系统中单元发生k次故障的概率为

2)阶段2:无备件条件下故障。此时,单元发生故障次数大于k,没有备件,系统相当于不可修复系统。在(t,τ]时间间隔内,系统相当于不可修复系统,系统不可靠度为F(τ-t)(F(·)为系统不可靠度表达式)。
因此,在(0,τ]时间间隔内,系统故障的概率为
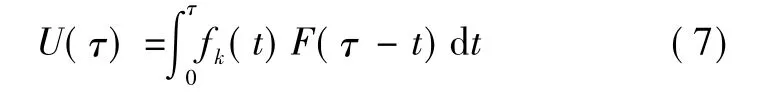
在(0,τ]时间间隔内,系统平均不能工作时间为
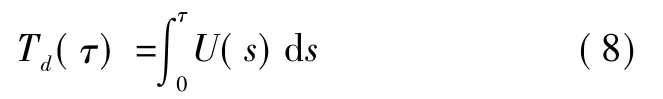
在(0,τ]时间间隔内,系统平均不可用度为
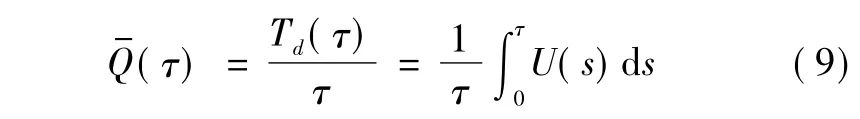
根据式(7)、式(8)或式(9),可进行系统备件数目分析。
由于r/n系统的不可靠度为
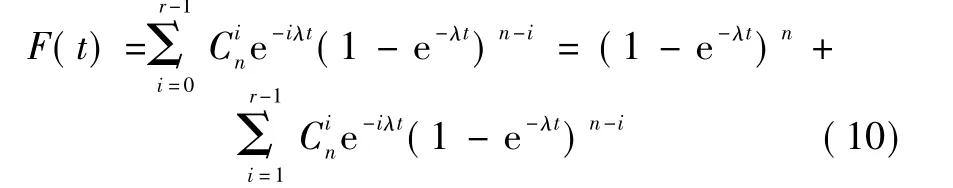
因此,
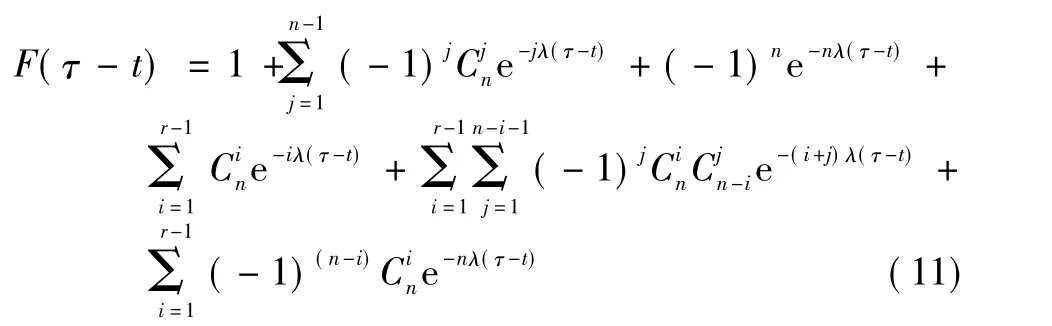
式(11)中:r为大于等于1的正整数;n为大于等于2的正整数。当r=1时是并联系统情况;当r=n时是串联系统情况。
将式(6)和式(11)代入式(7),可得在(0,τ]内系统故障的概率为
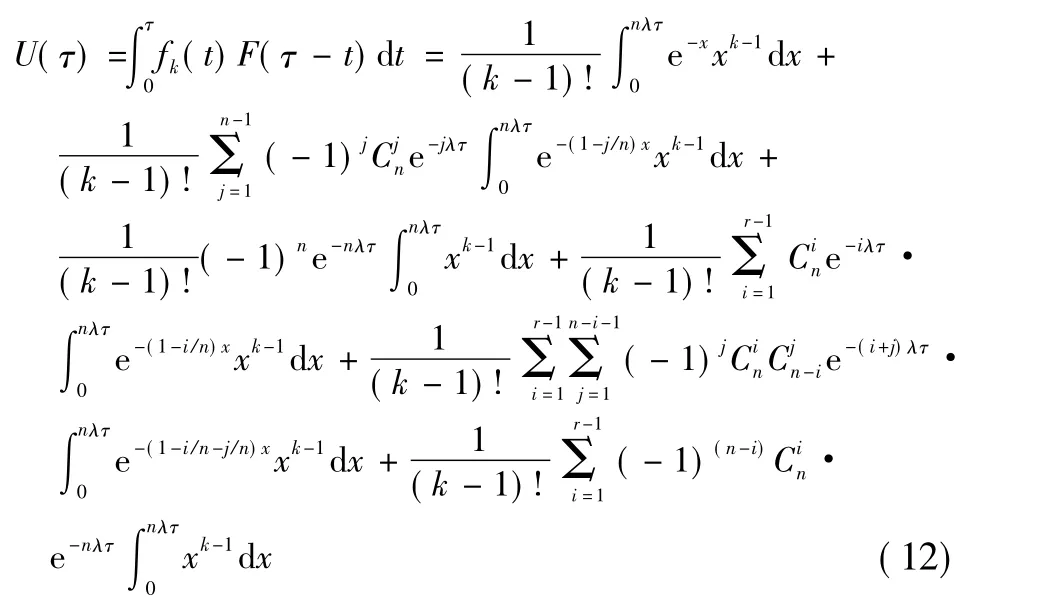
根据式(9),对上式再进行一次积分才可计算出系统的平均不可用度,可以预见,此特殊的被积分函数和二重积分计算过程将十分繁琐。针对此问题,首先采用积分变化,将式(12)转化为一般级数求和。
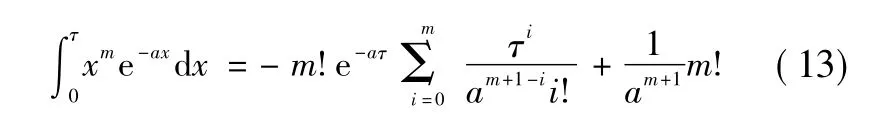
式中:m为大于等于零的正整数;a为大于零的实数。最后根据式(9),再利用式(13)积分变换,可计算系统平均不可用度的解析解
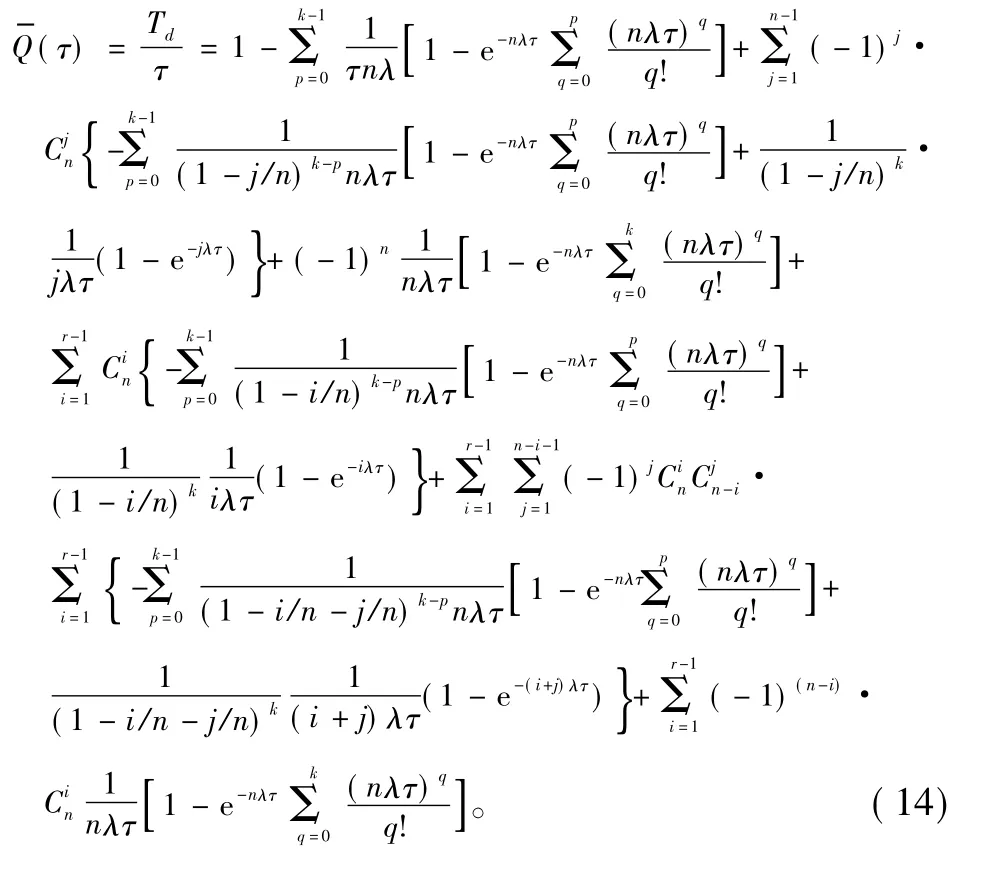
4 旁联系统的分析模型
除了上述讨论的r/n系统,在一般典型系统中,还包括一类系统即旁联系统。它由n个单元组成,任意时刻工作单元只有1个,(n-1)个单元处于备用状态。现假定系统工作单元故障,通过故障监测和转换装置(假定故障监测和转换装置的可靠度为1),切换到待用单元工作,同时更换故障单元,更换时间忽略不计。
若有k个备件的旁联系统故障,意味着(n+k)个单元依次全部故障,当每个单元的故障率为λ,根据泊松分布可知,在任意时刻t(t≤τ)的无限小区间dt内,单元发生(n+k)次故障的概率为
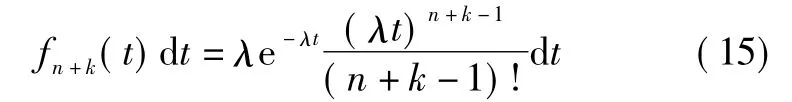
在任意时间区间[0,t]内,发生第n+k次故障的时间为Tn+k,发生第n+k次故障的概率为

对式(16)利用式(13)积分变化可得
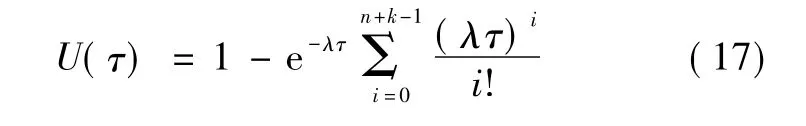
最后,根据式(4)和式(5),利用式(13)积分变化可得旁联系统平均不可用度解析解
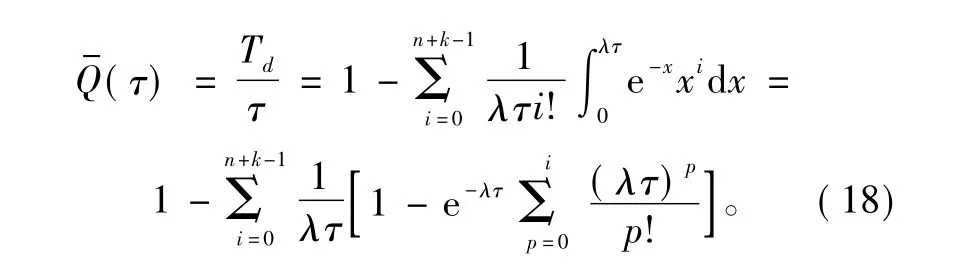
5 模型计算分析
一般一个典型系统可看作是由3~5个单元构成。这里,假定此r/n系统是由5个单元构成,当r=1(并联情况),r=3,r=5(串联情况),备件数量 k分别为1~5时,根据式(14),系统平均可用度A随λτ的变化情况分别如图2~图4所示。
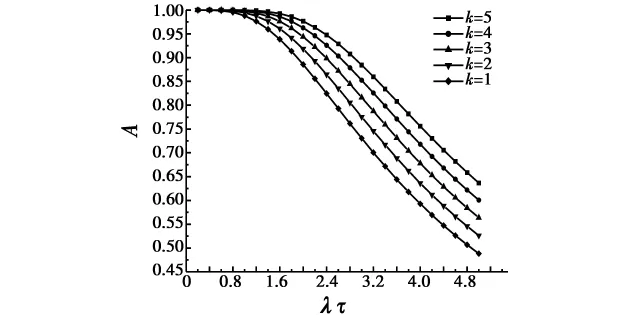
图2 r/n(r=1,n=5)系统平均可用度A与λτ关系Fig.2 The relationship between average availability A and λτ for r/n system(r=1,n=5)
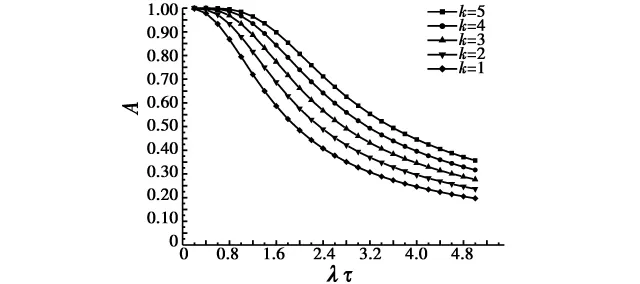
图3 r/n(r=3,n=5)系统平均可用度A与λτ关系Fig.3 The relationship between average availability A and λτ for r/n system(r=3,n=5)

图4 r/n(r=5,n=5)系统平均可用度A与λτ关系Fig.4 The relationship between average availability A and λτ for r/n system(r=5,n=5)
由图2~图4所示,可以方便快速地考察系统平均可用度A在不同备件数目k条件下随λτ的变化情况。同时,当单元故障率和时间已知的情况下,根据系统的构成情况,可以分析此r/n系统达到规定的可用度时所需最小备件数。例如,考察n为5,λτ为相应定值,系统平均可用度分别大于等于90%,95%和99%时所需的最小备件数量,结果如表1所示。

表1 解析法计算r/n(n=5)系统最小备件数Table 1 The minimum number of r/n system spare parts calculated by analytic method(n=5)
同样,对于旁联系统,根据式(18)即旁联系统平均不可用度的解析表达式,可以得到系统平均可用度A随λτ的变化情况。这里,假定此旁联系统由5个单元构成,当备件数量k分别为1~3时,系统平均可用度A随λτ的变化情况如图5所示。
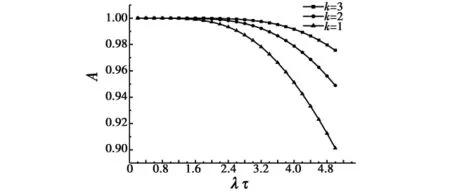
图5 旁联系统(n=5)平均可用度A与λτ关系Fig.5 The relationship between average availability A and λτ of on-off system(n=5)
根据图5可以快速查出,当n为5,λτ为相应值,系统平均可用度分别大于等于90%,95%和99%时所需的最小备件数量,结果如表2所示。

表2 解析法计算旁联系统(n=5)最小备件数Table 2 The minimum number of on-off system spare parts calculated by analytic method(n=5)
6 结论
针对蒙特卡罗仿真方法计算备件数量十分耗时且精度不高的问题,提出一种单元服从指数分布条件下典型电子系统备件数目确定的解析分析方法,通过分析可以得到以下结论:1)该解析解计算精度高,速度快;2)以平均可用度作为优化目标,将其与备件数量联系起来,更加符合工程实际;3)通过计算分析,对于可修复系统,在其他条件均相同的情况下,旁联系统的平均可用度大于并联系统平均可用度,且大于串联系统平均可用度的结论依然成立。
[1] DUBI A.蒙特卡罗方法在系统工程中的应用[M].卫军胡,译.西安:西安交通大学出版社,2007:53-58.
[2] DUBI A.The Monte Carlo method and optimization of spare parts in complex realistic scenarios[C]//Reliability and Maintainability Symposium,RAMS,2006:l649-1656.
[3] WIJARN W,LI Wenyuan,WAH S,et al.Applying probabilistic method in determining the number of spare transformers and their timing requirements[C]//Electrical and Computer Engineering,CCECE,2007:137-140.
[4] 王欢,陈永革,陈军.地空导弹装备战斗损伤概率的蒙特卡罗模拟[J].电光与控制,2009,16(5):58-62.
[5] 赵修平,夏长俊,罗轶,等.寿命服从指数分布的电子设备备件储备量的确定[J].海军航空工程学院学报,2006,21(4):426-428.
[6] SMIDT-DESTOMBES K S,HEIJDEN M C,HARTEN A.A-vailability of k-out-of-N systems under block replacement sharing limited spares and repair capacity[J].International Journal of Production Economics,2007,107(2):404-421.
[7] ABDEL H M.Inspection,maintenance and replacement models[J].Computers and Operations Research,1995,22(2):435-441.
[8] 李源,杨建军.导弹武器装备备件需求量分析与计算方法[J].兵工自动化,2007,26(8):22,34.
[9] 张涛,郭波,武小悦,等.任意结构系统的备件可用度评估模型[J].航空学报,2005,26(2):203-207.
[10] 魏艳华,王丙参,宋立新.与泊松过程有关的若干分布[J].内江师范学院学报,2010,25(10):31-34.

