基于模糊干扰观测器的无人机自主着陆逆控制器设计

程士广， 姜长生， 吴庆宪

(南京航空航天大学自动化学院，南京 210016)

0 引言

据统计，有人飞机在着陆阶段发生的飞行事故占到事故总数的一半以上，设计精确的着陆控制律对于飞机安全着陆非常重要，缺少驾驶员的无人机更是依赖控制律的作用。自主着陆控制技术已成为影响无人机发展和应用的关键技术。

无人机着陆阶段，无人机的动态模型具有显著的非线性和耦合特性，非线性动态逆的反馈线性化研究最为广泛，可以很方便地实现非线性对象的线性化和通道之间的解耦［1－2］。但是，动态逆控制要求被控系统能够精确建立数学模型，而且系统状态是可精确测量或者是可被估计的，这在实际系统中往往难以满足。干扰观测器结构简单、物理意义清晰，是处理不确定系统的重要方法;在干扰观测器设计中引入智能控制方法可以极大地改善观测器性能［3－4］。设计基于模糊逻辑的非线性干扰观测器既可以处理未知干扰和非线性系统不确定性，又增强了干扰观测器的自我调节能力，增加了控制器的鲁棒性。本文在无人机着陆飞行控制系统的快回路子系统各通道中引入模糊干扰观测器，利用干扰观测器逼近并补偿建模、求逆误差，降低了控制器对干扰和模型精确度的要求，增强了控制器的鲁棒性，改善无人机自主着陆控制。

1 建立数学模型

以无人机在地面坐标系中的位置x，y，z，无人机空速V，无人机迎角α、侧滑角β，无人机航迹倾斜角γ、航迹方位角χ、航迹滚转角μ，机体轴滚转角速度p、偏航角速度q和俯仰角速度r为状态量，建立无人机的6自由度12状态的非线性运动方程为［5］

式中:L，D，Y分别为所受空气升力、阻力和侧力;l，m，n分别为无人机机体轴的滚转力矩、俯仰力矩、偏航力矩;Tx，Ty，Tz分别为发动机在机体轴的推力分量;lT，mT，nT为相应的力矩;M为无人机质量。

2 自主着陆动态逆控制律设计

无人机自主着陆飞行是一个强耦合非线性系统，通过动态逆可实现对被控对象的解耦;根据时标分离的原则，将无人机系统分解为快慢不同的4个回路［6］，即快回路、慢回路、非常慢回路和极慢回路，这样将大大简化模型逆的解算。基于非线性动态逆的自主着陆飞行控制结构如图1所示。

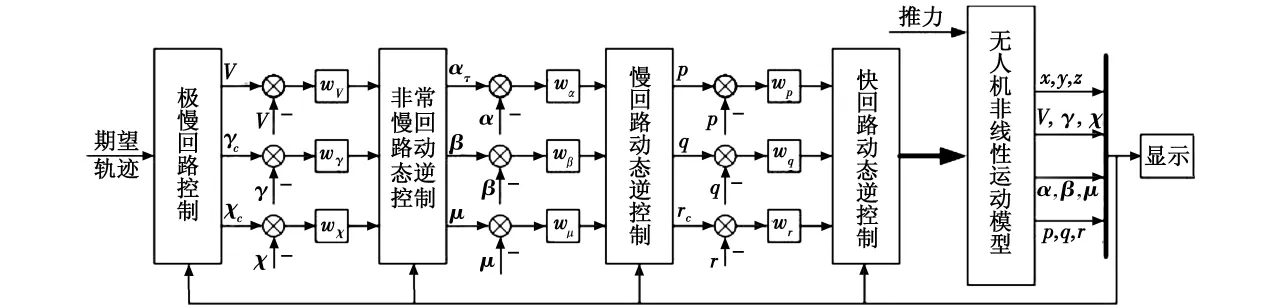
图1 无人机自主着陆非线性动态逆控制结构图Fig.1 DI control architecture of UAV autonomous landing

根据式(12)状态的非线性运动方程，可以写出各回路的仿射非线性方程。以快回路为例，其仿射非线性方程表达式为

由于快状态变量(p，q，r)对指令信号的响应非常快，可以认为它们的动态过程可以忽略，即在慢状态变量开始响应前，快状态变量已进入稳态过程，有p=pc，q=qc，r=rc。快回路设计的目标是对状态(p，q，r)进行线性化解耦控制，并构造快回路的逆控制律。使快状态回路具有如下理想闭环动态形式

式中:pc、qc、rc为慢回路控制律产生的指令信号;快回路的带宽 ωp、ωq、ωr均为 10 rad/s。

在快状态回路中，为了获得如式(14)所定义的期望角加速度，动态逆控制律u的表达形式为

同样，慢回路和非常慢回路的动态逆控制律也具有相同的形式，这里不再详述。

极慢回路使得无人机跟踪期望轨迹，实现轨迹控制。首先设计如下下滑轨迹

其中:初始下滑高度H0=250 m;下滑轨迹倾斜角γ=－3.5°;着陆点垂直速度为 －0.3 ～ －0.6 m/s;拉平高度 h0=15 m，hc=1.5 m。

在整个无人机着陆阶段，控制目标是保持无人机速度不变，跟踪设计的飞行轨迹。极慢回路输出的指令信号为:

3 基于模糊干扰观测器的动态逆控制器设计

动态逆控制要求控制方程必须已知，系统模型精确建立，然而实际的自主着陆控制系统，模型不确定和外部干扰必然存在，可以通过引入干扰观测器或模糊干扰观测器消除逆误差，降低动态逆对模型的依赖，提高系统的鲁棒性。

考虑一类含有系统不确定性和外界扰动的非线性系统［7－8］

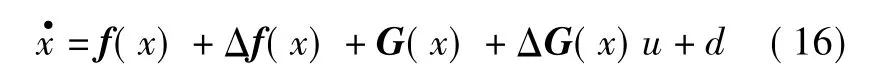
式中:x为系统状态;u为输入;f(x)为光滑非线性函数向量;G(x)为增益矩阵;Δf(x)，ΔG(x)为系统未知不确定项;d为未知外界扰动。用符号ψ(x，u)来表示系统的复合干扰 ψ(x，u)=Δf(x)+ΔG(x)u+d，一般不能精确得到复合干扰的解析表达式。利用模糊系统可以以任意精度逼近紧集上的连续非线性函数，设计基于模糊逻辑的干扰观测器来消除复合干扰的影响。

定理1考虑如下动态系统

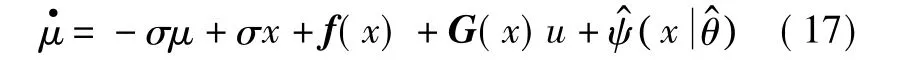
注1 ζ(x)为模糊基函数向量，本文其隶属度函数取高斯函数，表达式为［9］:

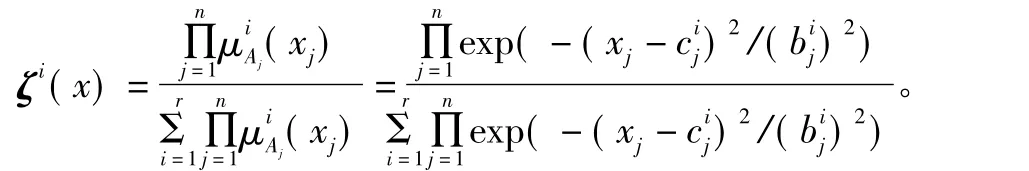
证明:根据式(16)、式(17)，可以得到FDO的观测误差动态方程

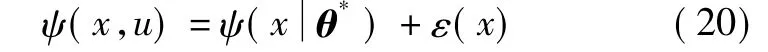
定义Lyapunov函数

式中，k＞0为系统设计参数。对函数求导得

图2是基于模糊干扰观测器的控制框图。下文定理给出带有模糊干扰观测器的动态逆控制系统闭环稳定性。

图2 基于模糊干扰观测器的控制框图Fig.2 Control block diagram based on FDO

定理2考虑式(16)所示非线性系统和式(21)所示观测误差动态系统，FDO的参数自适应调节律为式(22)，系统控制律为式(23)，则闭环系统跟踪误差一致最终有界［10－11］。

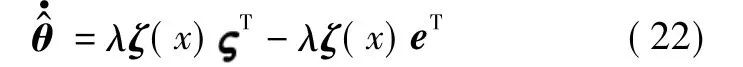
式中，λ为设计参数。

证明:定义跟踪误差e=xc－x，所以有

4 仿真及结果分析

为验证控制器的有效性，在快回路加入FDO观测回路不确定性。观测器动态系统的参数σ=15，自适应律的参数λ=1.2，采用7个模糊语言变量，隶属度函数为高斯函数，其中心分别取为 0.4，0.3，0.2，0，0.2，0.3，0.4，宽度均取为 1。

设定气动参数不确定性为20%，外界扰动干扰d(t)=sin(πt)(0.1，1，0.2)。仿真结果如图3 所示。

图3 无人机自主着陆仿真结果图Fig.3 Simulation result of UAV auto－landing

从仿真曲线可以看出，基于模糊干扰观测器的无人机自主着陆逆控制器取得不错的控制效果，有效消除干扰对飞行的影响，实现精确自主着陆控制，很好地完成对期望轨迹的跟踪，并保持无侧滑着陆。

5 结束语

对于无人机着陆模型的强耦合、非线性特点，采用动态逆的反馈线性化方法设计控制器，并基于时标分离原则将控制系统划分为四回路，大大简化求逆解算。针对单纯的动态逆控制器处理系统不确定性能力的不足，在控制回路中加入模糊干扰观测器，不但实现了对系统复合干扰的有效观测，还能在模糊自适应律调节下消除观测误差，提高系统的鲁棒性能。仿真证明，基于模糊干扰观测器的动态逆控制器能很好地实现对无人机的自主着陆控制。

［1］ 陈谋，姜长生，梅蓉.基于干扰观测器的新一代歼击机鲁棒飞行逆控制器设计［J］.飞行设计，2004(1):38－41.

［2］ 朱家强，朱纪洪，郭锁凤，等.基于神经网络的鲁棒自适应逆飞行控制［J］.控制理论与应用，2005，22(3):182－188.

［3］ KIM E.A fuzzy disturbance observer and its application to control［J］.IEEETransactionsonFuzzySystems，2002，10(1):77－84.

［4］ 陈谋，邹庆元.基于神经网络干扰观测器的动态逆飞行控制［J］.控制与决策，2008，23(3):283－287.

［5］ 陈谋.不确定非线性综合火力/飞行/推进系统鲁棒控制方法研究［D］.南京:南京航空航天大学，2004.

［6］ 陈龙胜.无人机自动起飞/着陆的控制技术研究［D］.南京:南京航空航天大学，2009.

［7］ KIM E.Output feedback tracking control of MIMO systems using a fuzzy disturbance observer and its application to the speed control of a PM synchronous motor［J］.IEEE Transactions on Fuzzy Systems，2005，13(6):725－741.

［8］ 陈谋，姜长生，吴庆宪.基于干扰观测器的一类不确定非线性系统鲁棒H∞控制［J］.控制理论与应用，2006，23(4):611－614.

［9］ 蒲明，吴庆宪，姜长生，等.基于模糊干扰观测器的自适应二阶动态滑模控制［J］.控制理论与应用，2011，28(6):805－812.

［10］ 黄国勇.基于Terminal滑模的空天飞行器再入鲁棒自适应控制［D］.南京:南京航空航天大学，2007.

［11］ LEU Yiguang，WANG Wei.Observer－based adaptive fuzzyneural control for unknown nonlinear dynamical systems［J］.IEEE Transactions on Systems，Man，and，Cyberneticspart B:Cybernetics，1999，29(5):583－591.