BP神经网络用于大视场显示设备的畸变校正

田立坤， 刘晓宏， 李 洁

(1.光电控制技术重点实验室，河南洛阳 471009; 2.中国航空工业洛阳电光设备研究所，河南洛阳 471009)

0 引言

在光电成像系统显示设备中，因为大视场光学系统本身特性的问题，光学系统引起的畸变影响了成像的几何位置，降低了光学显示系统的显示精度，恶化了显示画面的观察效果。为了取得更好的显示效果，国内外学者分别提出对数字像源画面进行像差几何校正的各种数学模型和校正方案来消除畸变带来的影响。文献［1］考虑了镜头的径向畸变特性，采用二元多项式法进行空间几何坐标校正，在摄像机标定过程中只需按照线性方法即可，因此运算速度快，适用于实时在线系统的标定，但校正精度有待提高。文献［2］认为可以先提取图像中的畸变曲线，通过优化畸变参数拟合线段的方法将曲线自动转换为理想的竖直线，此方法模型建立过程较为复杂，但较好地解决了大视场镜头的径向畸变问题。文献［3］根据图像对称的特点，将表达像素几何位置的直角坐标系转为极坐标系，该方法结合了CORDIC算法，比较适合在FPGA硬件平台上实现，较好地实现了图像畸变校正，适用范围较广。

对于大视场数字化显示器等复杂的显示设备，畸变特性模型未知而难以准确建立，所以本文提出双隐含层BP(Back－Propagation)神经网络方法进行畸变校正。该方法不需要预先确定样本数据的数学模型，仅通过样本数据的学习即可建立非线性映射关系，相对于传统神经网络算法具有更强的数据处理能力和更高的校正精度。

1 畸变校正基本原理

图像畸变校正需要解决的问题是确定非线性几何失真变换模型，目前较为常见的方法为多项式拟合法。设一幅显示设备几何失真后畸变图像的抽样点像素点坐标为(x，y)，校正图像中相对应的抽样点坐标为(u'，v')。畸变图像中任一点(x，y)与校正图像中对应点(u'，v')的变换关系表示为

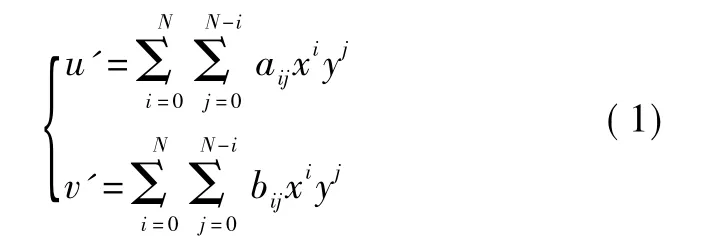
式中:aij和bij为多项式的系数;N为多项式次数。

多项式拟合法畸变校正模型是利用最小二乘法，以多项式为表达形式建立原始图像与校正图像的空间变换映射关系。畸变校正模型按照最小二乘法进行求解，均方误差表现形式［4］为

其中，L为抽样点的个数。对拟合误差平方和分别求导，求解出多项式拟合系数，得到误差均方和最小。即

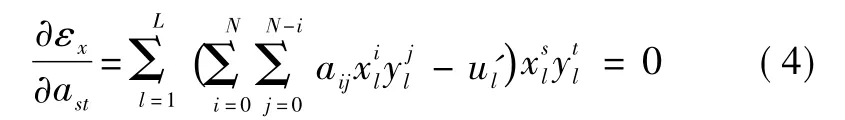
由此得到

式中:s=0，1，…，N;t=0，1，…，N － s;s+t≤N。令 M=1+2+…+N+(N+1)=(N+1)(N+2)/2。

常用的多项式拟合方法采用最小二乘法求解，计算量较大，计算过程中抽样点不宜选取过多。为了达到计算量与拟合精度的平衡，需要经过多次实验和比较才能得到最优校正效果的多项式拟合最高次数。由于校正精度不高以及灰度插值算法选择的原因，多项式拟合方法得到的校正图像会有图像退化的现象。

2 BP神经网络

2.1 BP神经网络原理

BP神经网络按拓扑结构分属前向网络，采用由导师训练反向传播的学习方法，实质上是一种梯度下降局部搜索算法，即利用梯度作为启发信息在局部范围内沿最优方向搜索局部最优点。传统BP神经网络是一种具有3层神经元的神经网络，包括输入层、隐含层、输出层。本文提出建立4层神经元的神经网络，即有双层隐含层，结构如图1所示，上下层之间实现全连接，而每层神经元之间无连接。当一对学习样本提供给网络后，神经元的激活值从输入层经各中间层向输出层传播，在输出层的各神经元获得网络的输入响应。接下来，按照减少目标输出与实际输出之间误差的方向，从输出层反向经过各中间层回到输入层，从而逐层修正各连接权值。随着这种误差逆向的传播修正不断进行，网络对输入模式响应的正确率也不断上升［5］。

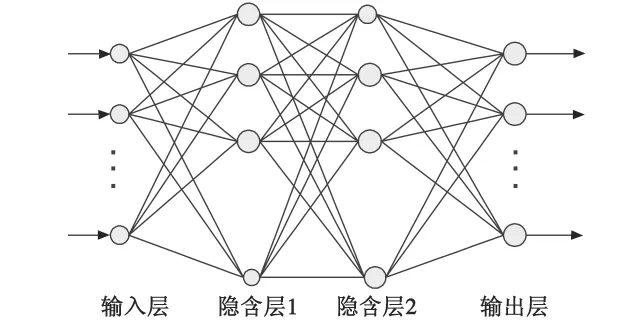
图1 BP神经网络结构图Fig.1 Structure of BP neural network

2.2 改进的BP神经网络

传统的BP算法有收敛速度慢、容易“陷进”局部极值等缺点，因此出现了很多改进的BP神经网络算法。BP神经网络改进主要有两种途径:一种是采用启发式学习算法;另一种则是采用更有效的优化算法。其中，基于数值优化理论的LM(Levenberg－Marquardt)算法收敛速度最快，而且精度也较高，故本文采用LM算法对神经网络进行训练。

设M个输入节点，L个输出节点，隐含层有q个神经元，则误差函数E为

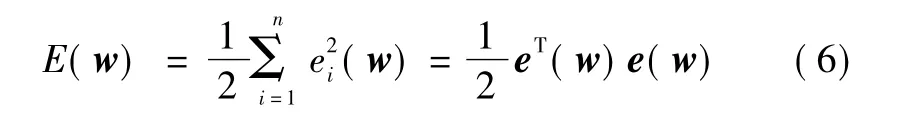
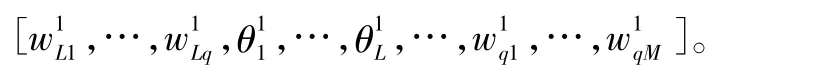
LM算法中权值和阈值的学习过程变换公式［6－7］为

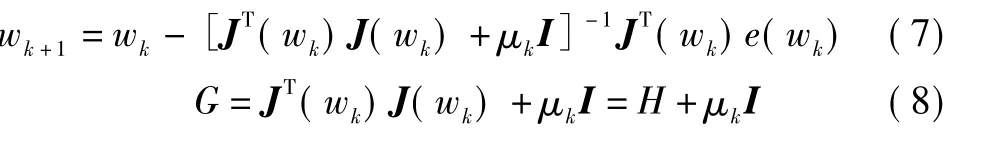
式中:μkI保证G可逆，否则JT(wk)J(wk)可能不可逆，无法计算;J(wk)为雅克比矩阵，含有网络训练误差的一阶导数，是权值和阈值的函数［8］。

LM算法训练方法是梯度下降法与高斯－牛顿法的结合，既有高斯－牛顿法的局部收敛性，又具有梯度下降法的全局特性。该方法依赖于μ的幅值，光滑地在牛顿法(当μ→0)和梯度下降法(当μ→∞)两种极端情况之间变化。采用LM优化方法，可以使学习时间更短，在实际应用中效果较好［9］。

由于现在的数字显示设备具有大视场、高像素等特点，这就需要处理大量的数据。基于LM算法的BP神经网络学习搜索能力和数据处理能力强，收敛速度最快，而且精度也较高，因此，本文提出了基于LM算法的双隐含层BP神经网络校正模型。

3 改进BP神经网络畸变校正模型

3.1 数据预处理

通过光学工程软件CODE V对数字像源分析，可均匀抽取设备显示畸变图像和像源原始图像21×21个抽样点作为样本数据［10］。数据表示形式为原始图像和显示图像抽样点的直角坐标，分别作为BP神经网络输入样本数据和输出样本数据。由于BP网络处理的数据数值相差较大，所以必须将样本数据进行归一化处理，以防止小数值信息被大数值信息所淹没。传递函数正切S型函数在值域［－1，－0.9］和［0.9，1.0］区域内曲线变化极为平坦，因此合适的归一化处理应该是将各输入物理量归至［－0.9，0.9］之间。通过以上分析可知，可以采用式(10)来进行归一化处理

式中，pi为图像 X 轴或 Y 轴坐标，i=1，2，…，441。

经过规格化后的BP神经网络样本数据为二维数组，数值全部在［－0.9，0.9］范围内，这样可以大大加快神经网络的训练速度。与此同时，在对BP神经网络模型进行仿真校正时，要对网络输出数据进行相应的反归一化处理，这样才能得到接近原始图像的校正图像。

3.2 确定神经网络结构

BP神经网络训练过程中，输入数据为畸变图像规格化后的二维数据，输出数据为原始图像反规格化前的二维数据，故输入层和输出层选择两个神经单元。为了加大处理数据的容量并提高畸变图像和原始图像之间的拟合精度，本文采用双层隐含层结构。隐含层的神经元数目选择是一个十分复杂的问题，往往需要根据设计者的经验和多次实验来确定，因而不存在一个理想的数学解析式表示。隐含层单元数目太多会导致学习时间过长、误差不一定最佳，也会影响网络的容错性。通过改变训练函数、学习函数等参数以及网络隐含层神经元的数目来观察训练情况，分析和对比后最终确定最优BP神经网络校正模型。分析实验结果可知，2－45－30－2拓扑结构建立的神经网络模型在此次研究的显示设备畸变校正中取得最优的校正效果。

传递函数是一个神经元及网络的核心。神经网络传递函数分为线性型、对数S型传递函数、正切S型传递函数3种。S型传递函数具有非线性放大增益，对任意输入的增益等于在输入曲线中该输入点处的曲线斜率值。本文采用正切S型传递函数［11］

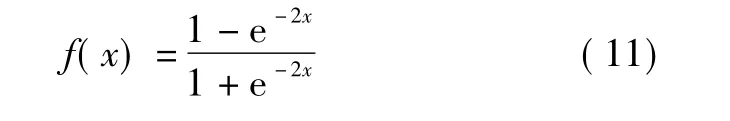
f(x)的值域为［－1，1］，此函数导数的值域为［0，0.25］，f(x)输出要达到±1附近很困难，这意味着可通过将输出数据控制在［－0.9，0.9］范围内的办法来提高训练速度和精度。

4 实验结果与分析

4.1 精度指标

为了比较文献［10］中多项式拟合方法与本文双隐含层BP神经网络畸变校正方法，本文以3种指标综合、全面地衡量空间变换所能达到的校正精度。

1)偏移距离。

水平方向为

垂直方向为

偏移距离直观地给出空间变换的校正误差，可以偏移距离的最大值Exmax和Eymax作为校正精度指标。

2) 均方根误差［12］。

均方根误差用ERMS表示。

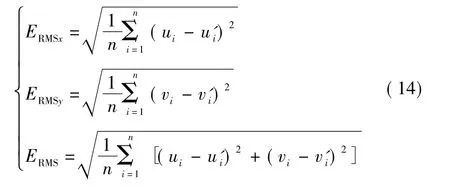
均方根误差反映了校正图像与原始图像偏离的程度。

3)全视场范围拟合位置精度［8］。

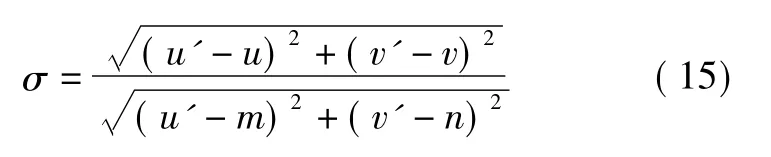
即原始抽样点(u'，v')到校正后对应点(u，v)的距离D2与原始抽样点(u'，v')到视场中心点(m，n)的距离D1的比值，其中，视场中心m=0，n=0.584。此精度指标更符合大视场显示设备的畸变特性。

4.2 实验仿真与分析

利用Matlab提供的BP神经网络工具箱，在Matlab7.1平台上进行仿真。改进的BP神经网络选取网络拓扑结构为2－45－30－2，训练函数为trainlm，学习函数为learngd，经296次训练后收敛。仿真结果表明，本文提出的双隐含层BP神经网络校正模型收敛速度和收敛精度达到非常好的效果，完全满足预期要求，即X轴、Y轴最大偏移距离E≤10－4，均方根误差ERMS≤10－6，平均全视场范围拟合位置精度δ≤10－5。训练结果如图2所示。

图2 改进的BP神经网络训练结果Fig.2 Result of improved BP network training

双隐含层BP神经网络校正图像前后仿真图如图3和图4所示，校正图像与原始图像在空间位置上十分相近。

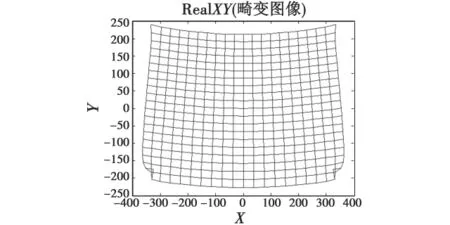
图3 畸变图像Fig.3 Distorted image

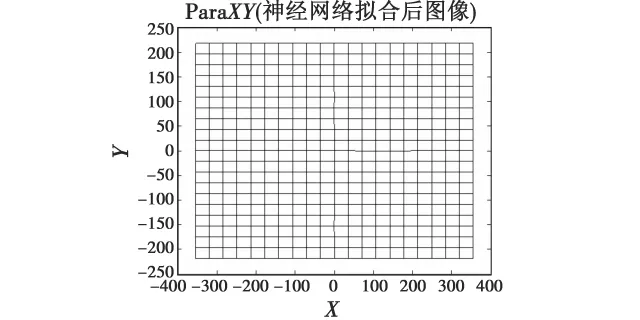
图4 改进的BP神经网络校正图像Fig.4 Corrected image of improved BP network

实验结果表明:为了达到计算量与拟合精度的平衡，传统多项式拟合校正模型最优最高次数N=8。由表1可以看出，多项式拟合校正前后21×21抽样点X坐标和Y坐标最大偏移距离分别为8.690×10－2mm和2.154 ×10－1mm，均方根误差为1.651 ×10－3。而基于双隐含层BP神经网络畸变校正模型的抽样点校正前后X坐标和Y坐标最大偏移距离精确到3.498×10－8mm和2.830 ×10－8mm，均方根误差达到 2.035 ×10－10。平均全视场范围拟合位置精度也由7.06×10－3提高到2.195×10－9。综上可知，与传统多项式拟合方法相比，双隐含层BP神经网络校正模型的各项精度指标提高明显，校正效果达到预期目标。

表1 BP神经网络法与多项式拟合法校正精度比较表Table 1 Precision comparison for BP network method and polynomial fitting method

5 小结

BP神经网络具有自学习、自组织、较好的容错性和优良的非线性逼近能力，可以在不确知畸变数学模型情况下，建立畸变图像与原始图像之间的高精度映射关系，实现相对简单。双隐含层BP神经网络算法相对于其他校正方法处理数据能力更强，校正精度优势明显，故BP神经网络畸变模型适用于精度要求较高的显示设备，对工程应用具有一定的指导意义。为了提高双隐含层BP神经网络处理数据速度，可以尝试将神经网络与其他优化算法如粒子群算法、遗传算法相结合，进而在硬件平台达到实时性图像畸变校正，这方面有待进一步研究。

［1］ 林慧英，苏建，刘玉梅.基于图像畸变矫正的摄像机标定方法［J］.吉林大学学报，2007，37(2):433－437.

［2］ SONG G Y，LEE J W.Correction of radial distortion based on line－fitting［J］.International Journal of Control，Automation and Systems，IEEE，2010，18(3):615－621.

［3］ LIN Qiang，ALLINSON N M.Spatial optical distortion correction in an FPGA［J］.Signal Processing Systems Design and Implementation，IEEE，2006，6:268－273.

［4］ FAN Xintian，SUN Qiang，LU Zhenwu.The geometric distortion correction of uncooled large－sized relative aperture infrared imaging system［J］.Infrared Components and Their Applications，SPIE，2005，5640:391－395.

［5］ 王洪元，史国栋.人工神经网络技术及其应用［M］.北京:中国石化出版社，2002.

［6］ CHU C，WIDJAJA D.Neural network system for forecasting method selecting［J］.Decision System，1994(12):13－14.

［7］ 王自强，李银妹，楼立人，等.BP神经网络用于光镊力的非线性修正［J］.光学精密工程，2008，16(1):6－10.

［8］ 侯亚丽，李铁.基于LM优化算法的BP神经网络目标识别方法［J］.探测与控制学报，2008，30(1):53－57.

［9］ 董厂虹.Matlab神经网络与应用［M］.北京:国防工业出版社，2005.

［10］ 郑春，周拥军，温永强.大视场光学显示设备图像畸变校正算法［J］.电光与控制，2011，18(5):23－27.

［11］ 史泽林，康娇，孙锐.基于BP神经网络的大视场成像畸变校正方法［J］.光学精密工程，2005，13(3):348－353.

［12］ ZHAO Xiaochuan，LUO Qingsheng.An image distortion correction algorithm based on quadrilateral fractal approach controlling points［J］.IEEE，2009:2676－2681.