紧凑型四反射镜光学系统设计

陈建发， 王合龙， 刘 欣， 潘枝峰

(1.光电控制技术重点实验室，河南洛阳 471009;2.中国航空工业洛阳电光设备研究所，河南洛阳 471009)

0 引言

在现代战争中，高空无人侦察机已成为侦察卫星和有人侦察机的重要补充和增强手段，无人侦察机具有成本低、侦察地域控制灵活、可昼夜持续侦察等特点［1］。由于无人机的载荷重量和体积对其续航时间长短和隐身性能优劣有很大影响，因此用于无人机的光电侦察系统，要求尽可能的小型化和轻量化。无人机一般都要求特定的飞行高度和对地最小分辨率。当飞行高度和探测器尺寸一定时，增大焦距可以提高对地面像元的分辨率［2］。但是，当焦距增大时，光学系统的尺寸也将随之增大，难以满足无人机对光学系统小型化和轻量化的需求。因此在既增大焦距又保证成像质量的条件下，如何尽量减小光学系统的体积已成为目前航空侦察光学系统研究的热点。

在大孔径的系统中，一方面折射系统需要采用特殊的材料和结构来消除二级光谱色差，另一方面，用于红外波段的透射材料尺寸不可能做得很大。而反射镜材料比透射镜材料更容易得到，尤其是大尺寸的。镀铝或介质膜的反射层，在很宽的波段范围内有很高的反射率，没有色差［3］。

由于二反系统不能满足大视场、大相对孔径的要求［4］，人们又引进了三反系统。共轴三反系统在大视场的情况下，中心遮拦过大，影响了进入系统的能量，从而降低了光学系统的分辨率，于是采用离轴三反系统能够解决中心遮拦问题［2，5－6］。然而当光学系统相对孔径为F/5～F/6，并且要求其工作距离小于焦距的0.25～0.3时，三反系统将无法满足这样的设计需求。此时就需要设计更为紧凑的四反射光学系统［7－10］。

传统四反射镜光学系统设计，一般都是先设计好三反射镜光学系统，然后在系统的中间像面处加入一场镜，从而构成四反射镜系统［7，9－10］。这种方法一般只能校正系统的球差、慧差、像散。设计初期，无法考虑系统的畸变［8］。

本文推导了基于PW方法的四反射镜光学像差理论。在依据平场条件选择四镜的半径的基础上，该方法可同时校正包含球差、慧差、像散、场曲和畸变5种像差。依据该理论给出了设计实例。光学系统满足轻量化、小型化的设计要求，像质的评定结果表明，光学系统成像质量接近衍射极限。

1 四反射镜系统初始结构参数求解

单色像差一共有5种:球差、慧差、像散、像面弯曲及畸变，其三级像差系数分别为 S1、S2、S3、S4及 S5。三级像差理论给出单色像差的表示式为

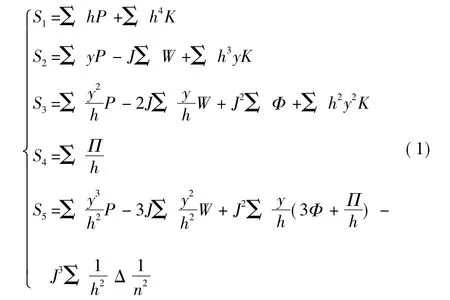
以上也适用于四镜系统，假定:物体位于无穷远，即l1=∞，u1=0;入瞳位于主镜上，即x1=0，y1=0。四反射光学系统光路见图1，其主镜M1、次镜 M2、三镜M3和四镜M4的二次非球面系数分别为

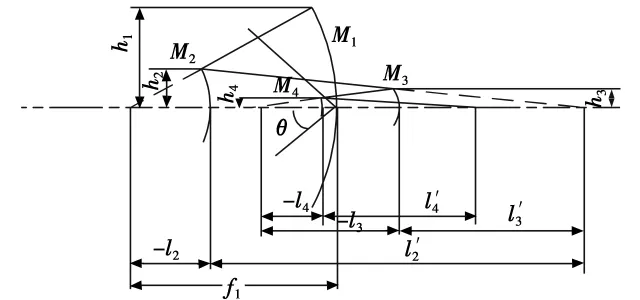
图1 同轴四反射镜结构图Fig.1 Systematic structure of the four－mirror system

各参数的物理意义如下:αi为该镜对于前一面镜子的遮拦比;βi为该镜对于后一面镜子的放大率;ri为每个镜面的半径;d1为该镜到后一面镜子的距离;hi为边缘光线在各个镜面上的入射高度;yi为主光线在各个镜面上的入射高度;Ki为各个镜面归一化非球面系数;Pi为各个镜面的球差系数;Wi为各个镜面的慧差系数。

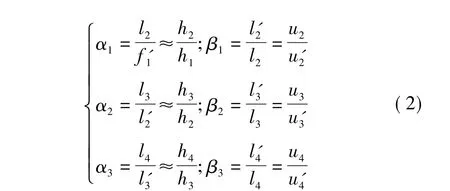
轮廓参数亦可用系统的结构参数r、d表示为

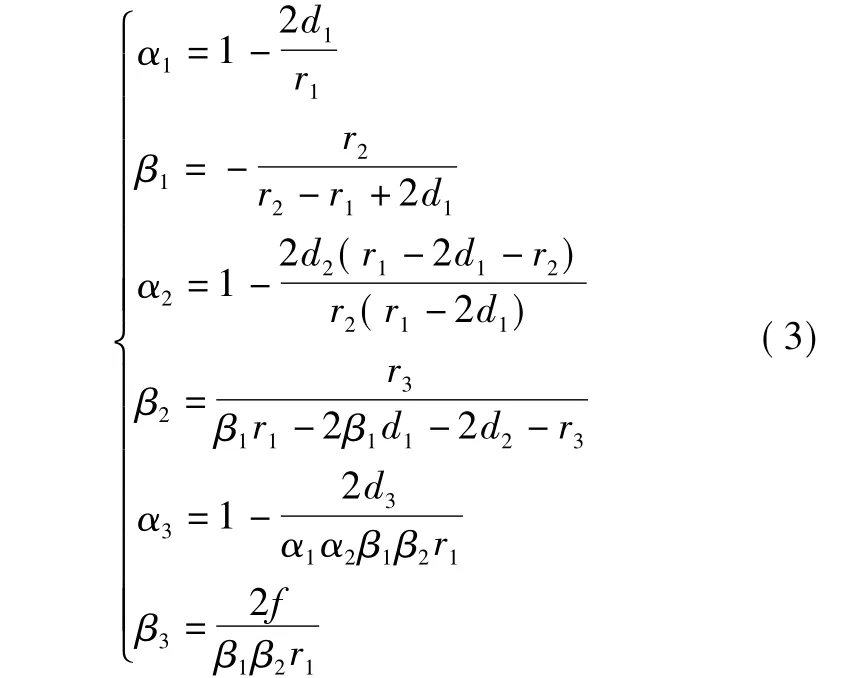
对于反射系统，n1=n'2=n3=n'4=1，n'1=n2=n'3=n4= －1，令h1=1，f'=1及 θ= －1，当光阑位于主镜时

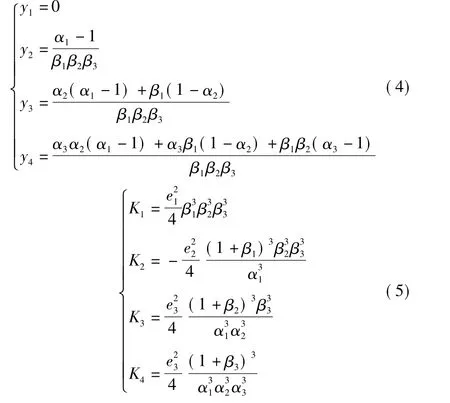
此外可以算得

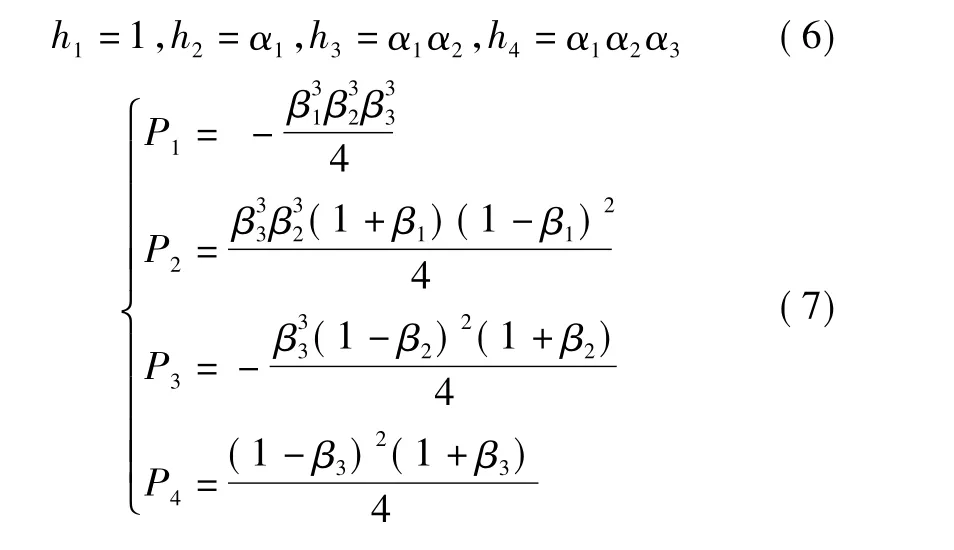
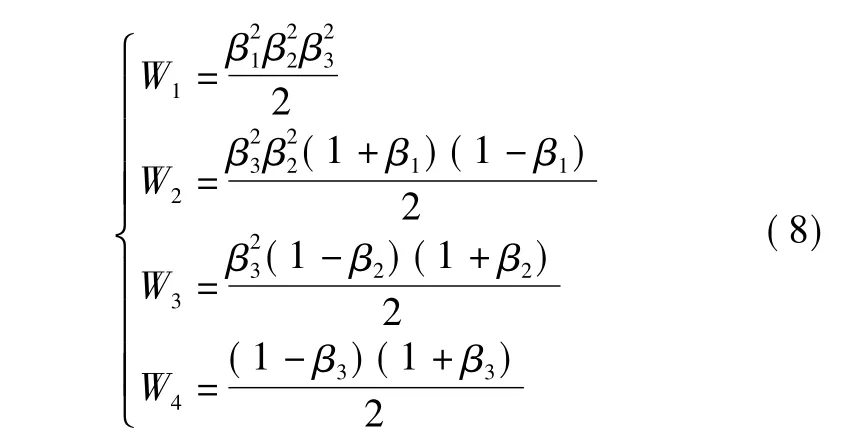
将以上各参数，带入式(1)，令5种单色像差为零，可得到平场曲条件式(9)和非球面系数的线性方程组(10)。

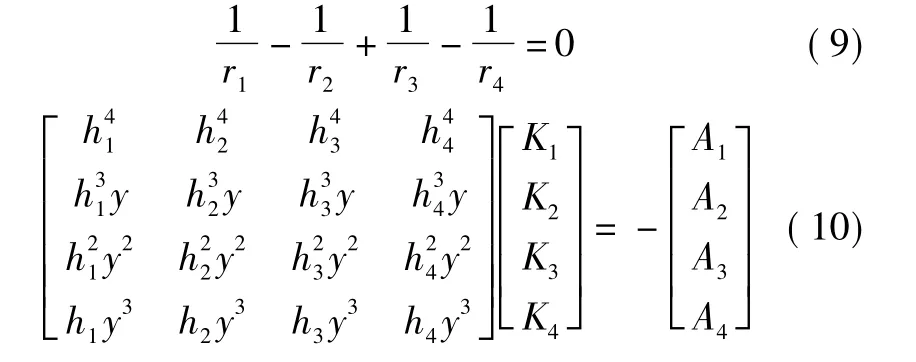
通过求解线性方程组(10)，可得到球差、慧差、像散和畸变为0时4个镜子的非球面参数，此时即可确定一个四反射镜光学系统的初始结构。

四反射镜光学系统的设计步骤总结如下:

1)系统一般都会给出系统总长度l和后截距d4，为了使得系统更加紧凑，三镜间隔一般大致相等，因此各个镜间间隔即确定为d1=d2=d3＜l;

2)依据系统要求的F数、系统焦距和平场曲条件(9)确定各个镜子半径ri的合理的取值;

3)由系统结构参数ri、di，依据式(3)可求得轮廓参数 αi、βi;

4) 由轮廓参数即可算得 hi、yi、Ki、Pi、Wi等参数，带入式(10)，即可解得各个镜子的非球面参数

文中采用Matlab语言对上述步骤进行编程实现。

在同轴系统优化设计初步完成后，可以对该系统进行光阑离轴或视场倾斜，直至完全消除中心遮拦，进一步做优化设计，到系统像质满足设计要求为止。这样，基于赛德尔像差的四反射镜光学系统的方案设计工作就基本完成了。

2 设计实例

2.1 光学系统设计指标

下面给出一个设计实例，系统设计参数见表1。

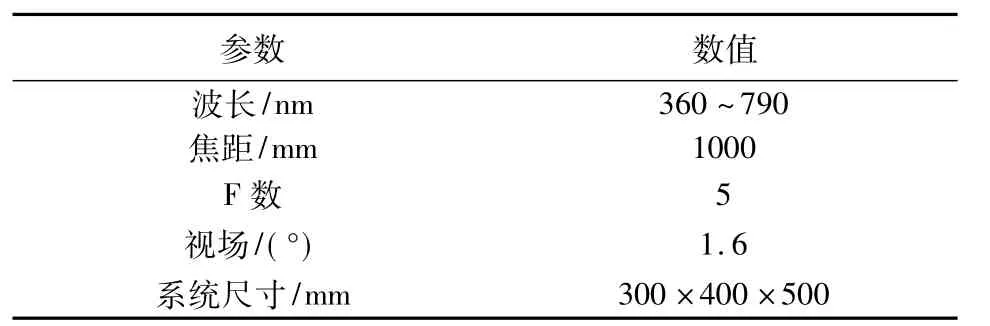
表1 光学系统设计参数Table 1 Design parameters of the optical system

2.2 光学系统设计及性能分析

根据以上理论及方法，设计好同轴四反系统，然后加入光阑离轴及限制条件，采用光学设计软件CodeV优化得到成像质量良好的无遮拦离轴四反射镜光学系统。系统MTF在50 lp/mm时边缘视场0.8左右，像质接近衍射极限。系统优化后参数如表2所示，光阑离轴量－25 mm。

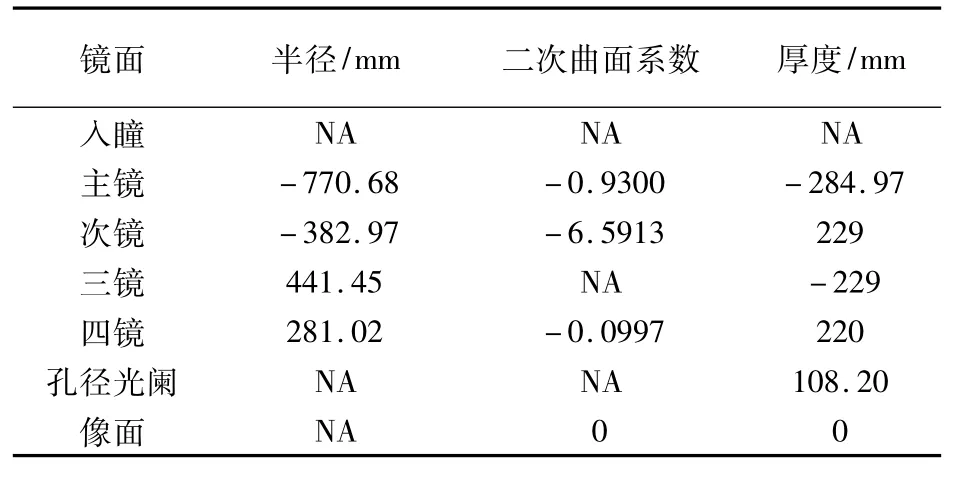
表2 优化后的离轴四反结构参数Table 2 Optimized parameters of four-mirror anastigmat optical system

表1中曲率半径r，由球面顶点算起到球心，从左向右为正，由下向上为正，反之为负;NA表示Not Available，即该值不可提供。

离轴四反结构如图2所示。

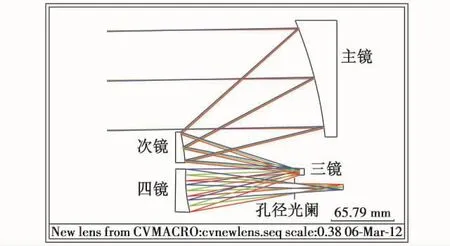
图2 离轴四反结构图Fig.2 Four－mirror anastigmat system layout

光学传递函数MTF如图3所示，在50 lp/mm时边缘视场0.8左右，成像质量接近衍射极限。

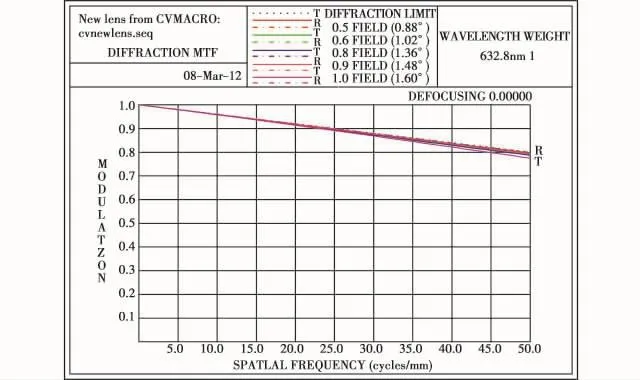
图3 系统MTF图Fig.3 MTF curves of the system

光学系统的点列图，如图4所示，最大弥散斑半径小于 1 μm。

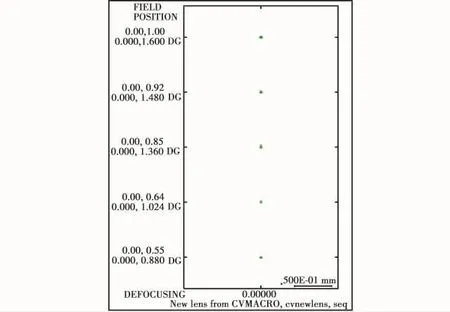
图4 系统点列图Fig.4 Spot diamgram of the system

光学系统的场曲与畸变如图5所示，最大场曲约为0.15%，最大畸变量约为1%。

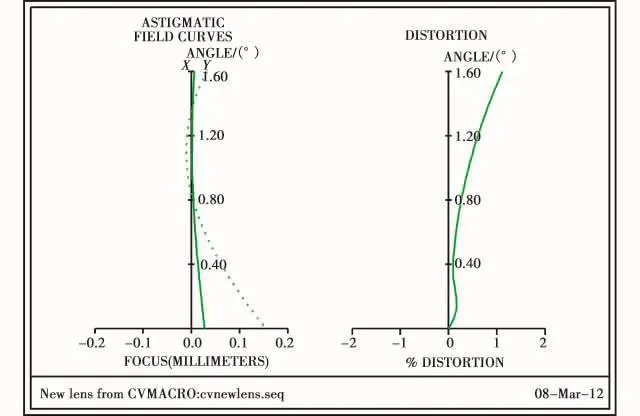
图5 系统的场曲与畸变Fig.5 Field curves and distortion of the system

像质的评定结果表明，光学系统成像质量接近衍射极限，各种像差得到良好校正。在该设计中，将光阑放在四镜之后，系统的出瞳位于系统焦平面之前，在出瞳处放置视场光阑，可有效地抑制杂散光。

3 结论

由于无人机的载荷重量和体积对其续航时间长短和隐身性能优劣有很大影响，因此要求用于无人机的光电侦察系统尽可能小型化和轻量化。离轴四反射镜系统可以提供更为紧凑的光学构型，保证了无人机对光学系统轻量化和小型化的设计需求。基于初级像差理论的四反射镜光学系统的设计方法，有利于在工程实现设计初期，通过计算选择一个较好地满足系统各项指标的初始结构，从而保证最终优化系统的成像质量。计算机辅助装调的发展简化了复杂光学系统的装调，紧凑型四反射镜系统将更为广泛地应用于航空侦察光学系统。

［1］ 刘鹏，彭艳鹏，邹秀琼，等.我国无人机航摄系统现状和前景［J］.地理空间信息，2010，8(4):158－161.

［2］ 姚罡，黄颖，傅丹膺.一种易于制造、较大视场离轴三反光学系统设计［J］.航天返回与遥感，2010，31(5):44－48.

［3］ 潘君骅.光学非球面的设计与检验［M］.苏州:苏州大学出版社，2004.

［4］ 刘剑峰，龙夫年，张伟，等.平像场无遮拦大视场两镜系统光学设计［J］.光子学报，2005，34(11):1659－1662.

［5］ 郭永祥，李英才，梁天梅，等.一种大视场离轴三反射光学系统研究［J］.光学学报，2010，30(9):2680－2683.

［6］ 刘辉，李兴隆，裴云天，等.离轴三反射式光学系统的设计［J］.激光与光电子学进展，2008，45(12):59－63.

［7］ COOK L G.Compact four－mirror anastigmat telescope:US，6767103B2［P］.2004:07－27.

［8］ LIANG Shitong，YANG Jianfeng，XUE Bin，et al.Design of a four－mirror optical system with wide field of view［J］.SPIE，2010，7849:1－6.

［9］ WANG Y J.Compact folded wide－angle large reflective unobscured optical system:US，5379157［P］.1995－01－03.

［10］ 丁学专，王欣，兰卫华，等.离轴四反射光学系统设计［J］.红外与激光工程，2008，37(2):319－321.