用塔康系统的区域导航定位算法

李晓东， 赵修斌， 王 啸

(空军工程大学信息与导航学院，西安 710077)

0 引言

塔康系统(Tactical Air Navigation System，TACAN)是军用标准近程无线电导航系统，作用距离为400～500 km，采用多瓣技术，极坐标体制定位，能在一种设备、一个频道上同时测向和测距。塔康测向原理与民航伏尔(VOR)信标相似，测距原理与测距仪(DME)相同。出于优化资源利用和军民融合的考虑，有些地区将VOR全向信标与塔康地面台合建于一处，称为伏塔克(VORTAC)，实现军民航共用塔康测距功能［1］。

为满足民航空中流量增加、经济高效和安全飞行的要求，国际民航组织(ICAO)提出了基于性能导航(PBN)方案，大力发展区域导航(RNAV)。不同于早期的航路导航围绕导航台对飞机进行极坐标定位，区域导航转而关注飞机与航路点及计划航线的相对位置关系。另外，PBN方案中的必备导航性能(RNP)规范要求机载设备具备实际导航性能监视能力［2－3］。

如果军用飞机能够实现区域导航，将大大提高飞行员的态势感知能力和作战效能，然而军机一般没有足够的空间容纳已发展成熟的民航设备，必须立足军用装备进行改进升级。出于战略安全考虑，军用飞机不能依赖美国军方主导的GPS全球卫星导航系统，而塔康系统可以为区域导航提供有力的装备支撑，即使在北斗二代全球导航系统建立之后，依然可以作为重要的备份导航源。

正常模式下，机载塔康设备主要测量飞机与塔康地面信标的斜距和信标台磁方位角进行极坐标定位，提供的导航信息相对较少，并且定位误差随着距离增大而显著增加，因而远远无法满足注重态势感知能力和高精度安全飞行的区域导航性能要求。本文针对此问题，提出塔康系统的3个改进点以适应区域导航需要:1)求解飞机与航路点的平面位置关系，并结合大气高程数据进行相应的坐标变换，得到飞机在地球坐标系下的三维位置估计;2)通过ρ-ρ测距平面定位提高定位精度，满足精确导航要求;3)位置估计与定位误差算法一体化，实现机载实时导航性能监测。最后通过数值仿真验证对其进行应用分析。

1 塔康系统在地球坐标系中定位

不同于传统的塔康极坐标定位模式，本文以目标航路点地面投影为原点，建立东北天坐标系及飞机位置量测方程，利用牛顿迭代法进行平面位置估计，结合大气数据中的高程信息进行坐标系变换，得到飞机在地球坐标系的三维位置估计。

1.1 以航路点为中心的东北天(ENU)坐标系下的位置解

1.1.1 单台定位:ρ-θ方式

以航路点W在水平面投影W'为坐标原点，建立东北天坐标系，假设飞机在过东向和北向平面上的投影为P'，塔康信标台投影点为T'，东北平面坐标系内三者的位置关系如图1所示。

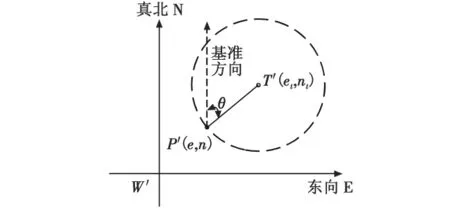
图1 东北平面坐标系Fig.1 EN reference frame

将P'与T'间距离真值记作r，用信标台磁方位角近似真方位角，记作θ。r和θ是飞机位置坐标e、n的函数，设r和θ的测量值分别为d、θc，不考虑测量误差的情况下，量测方程为

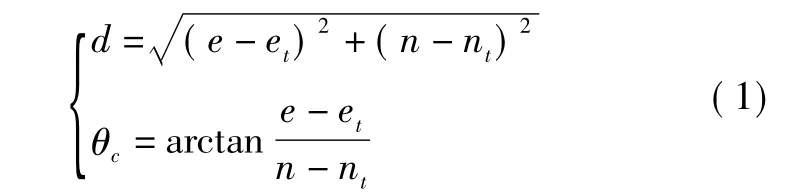
其中，(et，nt)表示塔康信标台在EN坐标系中的位置，通过飞行管理系统(FMS)和导航数据库可以预先解算和存储［4－5］。

由于牛顿迭代法具有计算量小、收敛速度快的优点，故本文采用该方法求解方程，基本步骤［6］如下所述。

1) 设飞机的初始位置为(ek－1，nk－1)，其与真值的误差分别为 Δe、Δn，即 e=ek－1+ Δe，n=nk－1+ Δn。其中，k=1，2，3，…，表示迭代次数。

2) 将测量方程在(ek－1，nk－1)点用泰勒级数展开，忽略二次及以上项，则有

由于式(2)左边为Δe、Δn的线性方程组，故将其变形可得

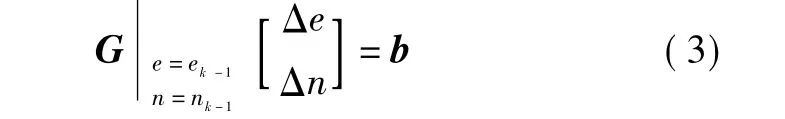
其中飞机坐标e、n的二元函数矩阵G为

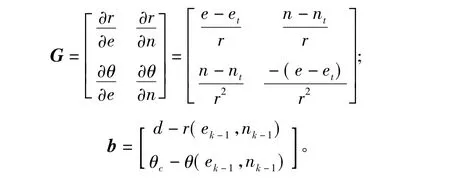
G满秩时则有

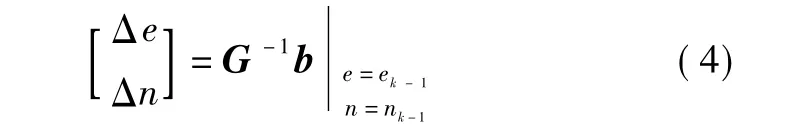
G只与信标台和飞机的相对位置有关，称为几何矩阵(也称为雅可比矩阵)。

4) 更新估计值 ek、nk，并重复 2)、3)步骤;ek、nk的更新值分别为

1.1.2 双台定位:ρ-ρ方式

当飞机航行范围内有两个或两个以上的塔康信标可用，理论上可以进行ρ-ρ测距定位(塔康测距原理与民航大量使用的测距仪相同，因而可以进一步考虑利用丰富的民航资源)。

同样在航路点投影为原点的东北天坐标系中，两个塔康信标台在东向和北向平面上投影为T'1(et1，nt1)、T'2(et2，nt2)，飞机在平面内投影 P'到信标台投影距离真值分别为r1、r2，设测量值分别为 d1、d2，暂时不考虑误差项，建立量测方程为

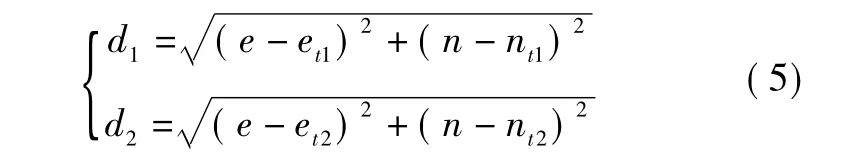
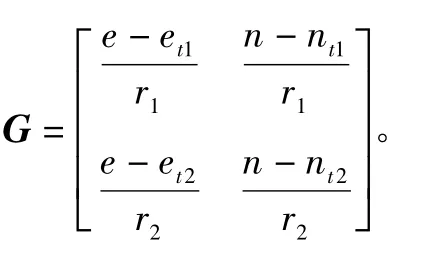
1.2 飞机在地心地固坐标系ECEF下的位置解

在通过塔康系统进行平面定位后，结合高程信息(如大气数据)，确定飞机在东北天坐标系中的天向坐标u，此时通过导航数据库获取航路点投影W'在大地坐标系下的经度λW，纬度φW信息，以及在地心地固参考系下的坐标(xW，yW，zW)T，则飞机在地心地固坐标系下的位置为

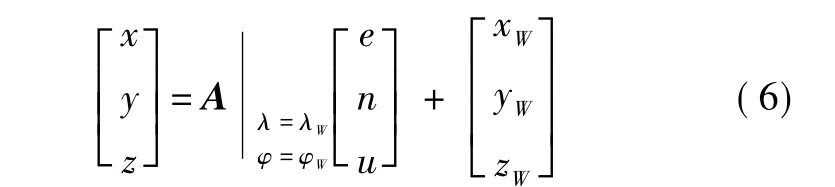
其中，坐标变换矩阵A为

代入W'处的经纬度λW、φW即可求解。需要指出的是，从飞机相对塔康信标的斜距和信标台方位角信息转换到飞机的地心地固直角坐标，对于区域导航来说具有重要意义:它提供了更多的导航定位信息，并且是计算相对于航线和目标航路点的偏航误差、理想航迹角、航程和斜距等区域导航参数的基础，此外，多导航传感器信息融合时，这一转换也是前端进行初始数据配准的重要步骤。

另外，还可以根据需要，通过坐标转换公式得出飞机直观的经纬高位置信息［7］。

2 实际导航性能评估

性能基导航PBN的RNP规范要求飞机可以实时评估导航位置估计误差，也称为位置不确定度(EPU)估计。本节主要对第1节所提出算法的定位误差进行分析。

2.1 投影误差

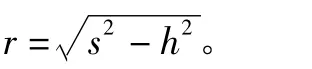
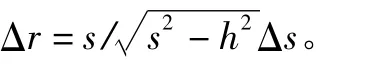
假设误差无偏，可推导得到误差传递公式为

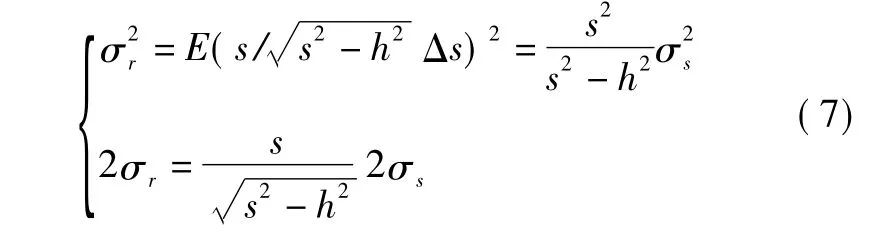
上式是平面定位误差分析研究的基础。不难看出，在保持巡航高度h不变的情况下，飞机与信标台距离越远，塔康测距误差与水平投影误差越接近;反之，飞机与信标台距离较近时误差变化波动较大。

2.2 平面定位误差

实际导航性能评估实质上就是机载设备实时计算定位误差的过程［8－9］，在第1节利用牛顿迭代方法解非线性方程组时，得到几何矩阵G，位置解算过程结束的同时就可以利用它进入定位误差的计算。

2.2.1 ρ-θ方式定位误差分析

当保留塔康测向误差和测距误差项时，相应地引起塔康与飞机水平距离r的误差为εr，塔康信标方位角θ的误差为εθ，则有

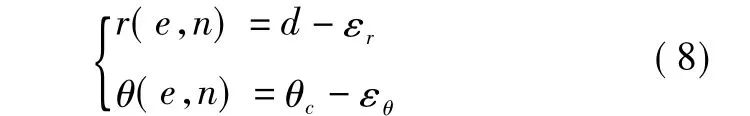
假设定位误差均很小，对方程组线性化的影响可以忽略不计，并且在进行第k+1次迭代时收敛，飞机的位置坐标此时变为已知量，即:e=ek+Δe，n=nk+Δn。

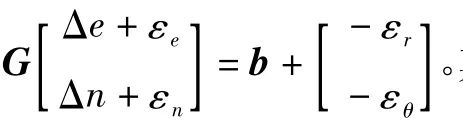
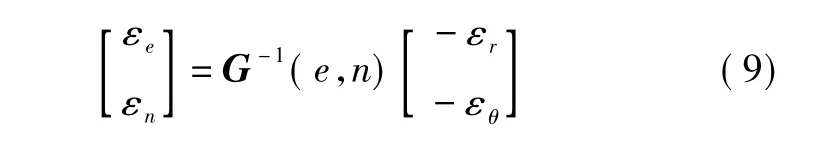
上式表明了测量误差和定位误差的关系。假设各个测量误差εr、εθ均呈相同的正态分布，均值为0，方差为σ2，且各测量误差互不相关，则有

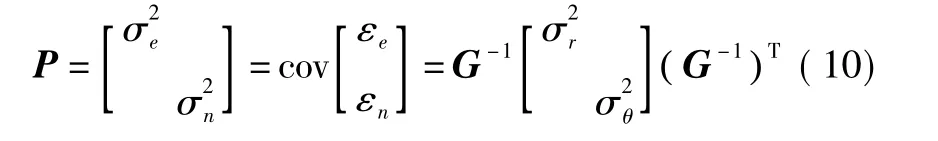
进一步可得标准定位误差为

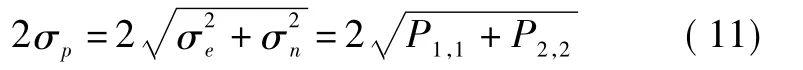
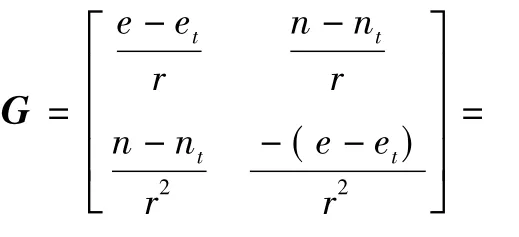
2.2.2 ρ-ρ方式定位误差分析

设测量误差 εd1、εd2，与 ρ-θ方式类似，可以得到

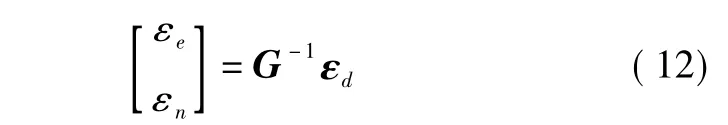
式(12)表明了定位误差量和测量误差量的关系。不难看出，飞机与信标台的相对位置是影响定位精度的重要因素。θ1、θ2表示两个信标台方位角估值，定位解算前可以用机载塔康系统的输出量测值近似，从而很方便地估计几何矩阵G以及标准定位误差。

假设测距误差εd1、εd2均呈正态分布，均值为0，且不相关，计算定位误差协方差阵为

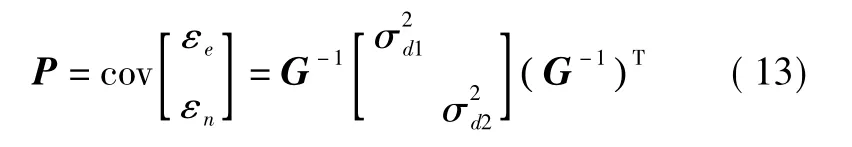
标准定位误差为

进一步假设测量误差量εd1、εd2的方差都为σ2时，则有

D定义为权系数矩阵，利用三角函数关系合并化简，得权系数矩阵的迹为

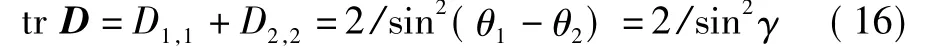
其中，γ表示飞机与两个信标台连线投影水平面的夹角，权系数的迹也可称为几何误差因子GDOP。标准定位误差可以表示为

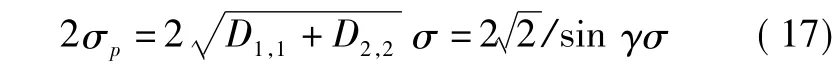
2.3 坐标转换误差分析

计算坐标转换误差协方差矩阵为

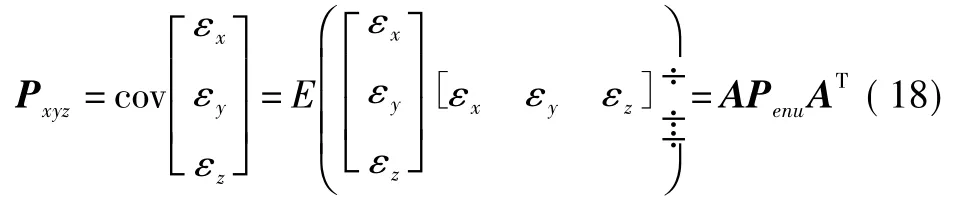
东北天坐标系到地心地固直角坐标的转换矩阵A为单位正交矩阵，即A－1等于AT，容易证明

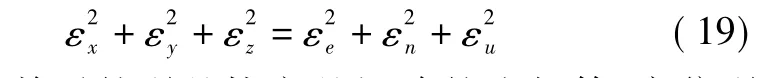
即坐标变换前后的误差协方差矩阵的迹相等，定位误差不变。

3 仿真验证及应用分析

参考某型塔康设备技术参数，设塔康的标准测角误差2σθ=2，标准测距误差2σs=200 m，飞机巡航高度10 km，塔康信标台在航路点东北天坐标系中位置确定，利用Matlab进行位置解算和误差仿真。

图2表示在保持巡航高度不变的情况下，随着飞机与信标台水平距离增大，水平距离误差由较大值快速下降，并逐渐逼近斜距测量误差;在60 km处，水平距离误差与斜距误差相差约为1%;需要说明的是，图中水平距离增大的过程实质上体现的是飞机仰角减小的过程，因而在塔康信标台信号覆盖范围内，飞行高度与定位误差没有直接关系，不直接影响算法的适用性。

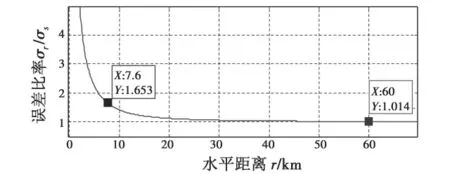
图2 σr/σs与r的关系Fig.2 Relation between σr/σsand r

图3 和图4是采用极坐标方式测角测距单台定位误差仿真分析。图3表示飞机与信标台水平距离为100 km时(斜距100.5 km)，信标台方位角由0变换至2π，定位误差恒定为较大值3.496 km，结合第2节的理论分析可以推断，当飞机与信标台投影距离r一定时，各个方向不同θ角处的标准定位误差均相同。

图3 标准定位误差2σ与信标台方位角θ的关系Fig.3 Relation between 2σ and θ

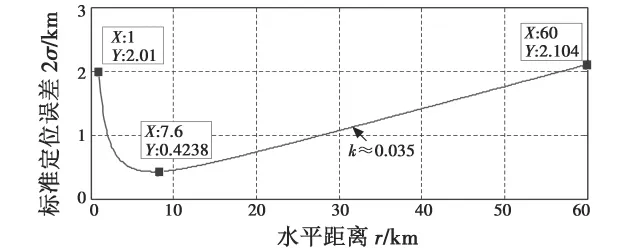
图4 ρ-θ模式标准定位误差2σ与r的关系Fig.4 Relation between 2σ and r of ρ-θ mode

图4 显示的是进行单台测角测距定位时，飞机保持巡航高度不变的情况下，标准定位误差2σ与水平距离r的关系。分析可得，飞机由塔康信标台水平距离1 km附近增加至7.6 km处，随着飞机与信标台的仰角逐渐减小，水平投影距离r的误差2σr迅速减小，导致定位误差由1.468 km急剧减小至0.5491 km，并取得极小值(此时投影距离误差并不是最小值，见图1);随着飞机进一步远离塔康信标台，水平投影距离测量误差受高度影响可以忽略，可看作某一常数值，定位误差与水平距离r呈近似线性递增关系，变化率约为0.035，即每远离信标台1 km，标准定位误差增加35 m。

图5和图6是采用双台测距平面定位的标准误差分析。图5表示在飞机与两个塔康信标台距离都超过60 km，忽略巡航高度对水平距离误差的影响时，标准定位误差与测距位置线夹角γ的关系。容易看出，曲线在90°处取得极小值0.28 km，并以其为中心左右对称。民航总局规定实施区域导航时，两个DME台站与飞机连线夹角应在30°到150°之间［10］，图中做出了相应的标注。

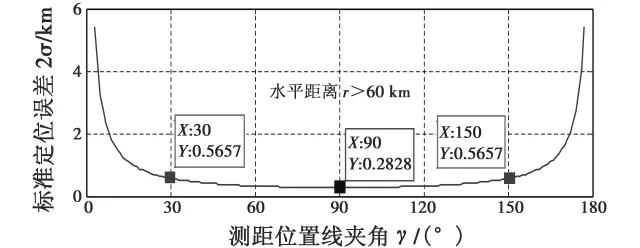
图5 标准定位误差2σ与位置线夹角γ的关系Fig.5 Relation between 2σ and γ

图6 表示的是测距位置线夹角为90°时，标准定位误差与水平距离的关系曲线，为控制变量，假设飞机与两个塔康信标台距离相等。可以看出，图6曲线与图2曲线在形状上具有一致性，正是由于水平距离误差在塔康信标附近的非线性导致了定位误差的跳变。

民航总局规定使用DME进行测距定位时，从DME台位置看，飞机与信标台仰角β应低于40°［10］，作为参考，图中标出了某型塔康装备在仰角40°处的标准定位误差值(约为0.3694 km)。

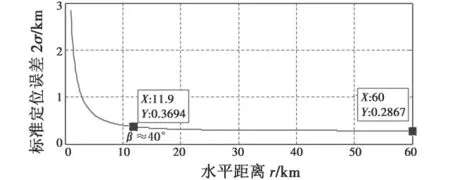
图6 ρ-ρ模式下标准定位误差2σ与水平距离r的关系Fig.6 Relation between 2σ and r of ρ-ρ mode

综合以上仿真图形，结合理论分析不难得出，塔康系统进行单台测角测距定位时，定位误差随信标距离的增大而增大，不适合平行航路的建立，也不能满足高精度的RNP类型的需要(例如，RNP2要求导航系统误差不能超过1 n mile，即1.852 km);双台测距定位在几何构型合理时有稳定且较小的定位误差，可以满足大多数的航路RNP类型的精度要求，但是相对空间位置不理想时，定位误差急剧跳变。因此，考虑以测距定位为主，当几何误差因子增大超出门限或者只有唯一的塔康信标台可用时，可以切换到单台测角测距定位。定位的同时在机载显示终端实时给出实际导航性能参数，以及相应的告警。

4 小结

在区域导航航路飞行中，将机载塔康设备看作导航传感器，输出斜距和信标台方位角信息，在东北天和地心地固坐标系下通过合理的重构和解析可以提供更加丰富和有效的位置信息和区域导航参数。理论分析和仿真表明，常规的测角测距定位方式因为随着与信标台距离的增大，定位误差不断增加，有些情况下不能满足区域导航平行航路以及精确导航的需要;可以考虑合理的技术改进，通过塔康组网实现双台甚至多台测距平面定位，从而提高定位精度;此外，与 VOR/DME不同的是，由于塔康测角工作频率较高，测角最大作用距离与测距是一致的，角度信息在机载实际导航性能监测中可以得到有效利用。

［1］ 张忠兴.无线电导航理论与系统［M］.西安:陕西科学技术出版社，1998.

［2］ ICAO.Performance Based Navigation(PBN)manual［S］.3rd ed.2008.

［3］ Federal Aviation Administration.Roadmap for Performance－Based Navigation［S］.Washington DC，July 2006.

［4］ HERNDON A A.Analysis of advanced Flight Management Systems(FMS)，Flight Management Computer(FMC)field observations trials:Area Navigation(RNAV)holding patterns［C］//Digital Avionics Systems Conference(DASC)，2011 IEEE/AIAA 30th，Oct.2011:1－17.

［5］ ATKINS S，CAPOZZI B.Relative position indicator for merging mixed RNAV and vectored arrival traffic［C］//Digital Avionics Systems Conference(DASC)，2011 IEEE/AIAA 30th，Oct.2011:1－13.

［6］ 田孝华，周义建.无线电定位理论与技术［M］.北京:国防工业出版社，2011.

［7］ 马霞.TACAN数据在惯导参数校正中的坐标变换［J］.电讯技术，2011，41(6):98－101.

［8］ CHAMLOU R.TIS－B:Calculation of navigation accuracy category for position and velocity parameters［C］//Proceeding of Digital Avionics Systems Conference，Salt Lake City，USA: ［s.n.］，2004，1:11－13.

［9］ 孙淑光，戴博，张鹏.机载组合导航系统实际导航性能计算方法［J］.控制工程，2011(3):262－266.

［10］ 中国民用航空局飞行标准司.AC－91－FS在航路和终端区实施 RNAV1和 RNAV2的运行指南［S］.北京，2008，6.