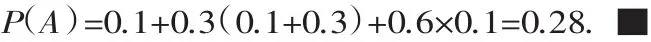应重视用枚举法解概率题

☉湖北省十堰市东风高中 甘志国（特级教师）

题1 某汽车站每天均有3辆开往省城的分为上、中、下等级的客车各一辆.某天干先生准备从该汽车站前往省城办事，但他不知道客车的等级情况，也不知道发车顺序.为了尽可能乘上上等车，他采取如下策略：先放过第一辆，如果第二辆比第一辆好则上第二辆，否则上第三辆，那么干先生乘上上等车的概率是______.

解：这里的一次试验是“每天均有3辆开往省城的分为上、中、下等级的客车各一辆”，试验成功的情形是“干先生采取上述策略能乘上上等车”.

题2（2010年安徽理21）品酒师需定期接受酒味鉴别功能测试，一种通常采用的测试方法如下：拿出n瓶外观相同但品质不同的酒让其品尝，要求其按品质优劣为它们排序；经过一段

时间，等其记忆淡忘之后，再让其品尝这n瓶酒，并重新按品质优劣为它们排序，这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.

现设n=4，分别以a1、a2、a3、a4表示第一次排序时被排为1、2、3、4的四种酒在第二次排序时的序号，并令X=|1-a1|+|2-a2|+|3-a3|+|4-a4|，则X是对两次排序的偏离程度的一种描述.

（1）写出X的可能值集合；

（2） 假设a1、a2、a3、a4等可能地为1、2、3、4的各种排列，求X的分布列；

（3）某品酒师在相继进行的三轮测试中，都有X≤2，

①试按（2）中的结果，计算出现这种现象的概率（假定各轮测试相互独立）；

②你认为该品酒师的酒味鉴别功能如何？说明理由.

解：这里的一次试验是“将1、2、3、4排序”，可以枚举出这A44=

24（种）排列及其对应的X值，如下表：

由此表立得本题的答案是：

（1）X的可能值集合为{0，2，4，6，8}.

（2）在等可能的前提下，得

注：从阅卷情况看，这道高考压轴题的得分率极低.笔者认为造成这种情形的主要原因是考生不会用最简单的原始方法——枚举法解决计数问题，只知道套用排列组合

公式解决复杂的计数问题，殊不知，用简单的枚举法也能轻松解决计数以及概率统计问题.

（1）设X表示目标被击中的次数，求X的分布列；

（2）若目标被击中2次，A表示事件“第一部分至少被击中1次或第二部分被击中2次”，求P（A）.

解：（1）略.

（2）我们先列举出目标被击中2次时被击中的部分的所有情形：

只有情形1、2、3、4、5、7满足题意，所以