为“数”配“形” 凸显数学思想
●卢 明 (元济高级中学 浙江海盐 314300)
1 问题的提出
在高中数学中,许多问题单纯用“数”的方法去解决较繁琐,若能从“形”着手,则会事半功倍.这就是数形结合思想在解决实际问题时的经典运用,其核心就是为“数”配“形”.需要指出的是,为“数”配上什么样的“形”,是运用数形结合思想解决实际问题时的一大难点.那么,有没有规律可寻呢?本文将对此作一些探索,以抛砖引玉.
2 利用常见函数模型构图
例1 设函数f(x)=(x-a)2lnx,a∈R.
(1)若x=e为y=f(x)的极值点,求实数a的值;
(2)求实数a的取值范围,使得对任意的x∈(0,3e],恒有 f(x)≤4e2成立.
(2011年浙江省数学高考理科试题)
下面仅对本题第(2)小题进行分析.
分析当 x=a∈(0,3e]时,f(x)=(xa)2lnx≤4e2显然成立.
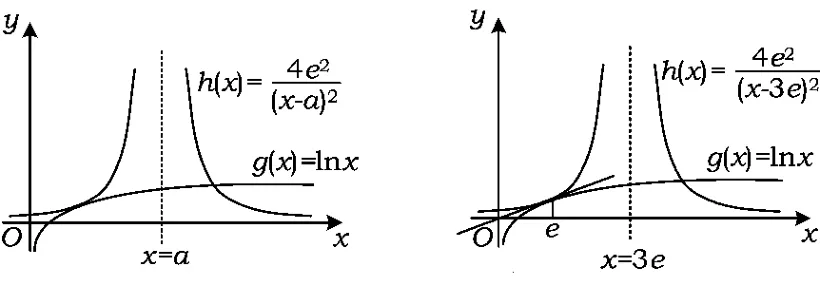
图1 图2
①若 a=3e,则

即函数g(x)与h(x)的图像有公共点(e,1).又因
由图2知,在(0,3e]上 g(x)的图像是上凸且递增的,h(x)的图像是下凸且递增的.因此,对任意的 x∈(a,3e]恒有 g(x)≤h(x),即 f(x)≤4e2.
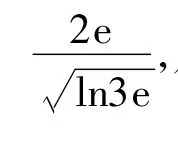

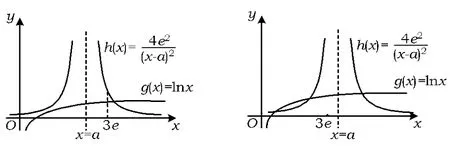
图3 图4
③若 a >3e,则由①知,在区间(0,3e)上,g(x)与h(x)的图像有交点,故不满足对任意的x∈(0,3e)恒有g(x)<h(x),如图4所示.
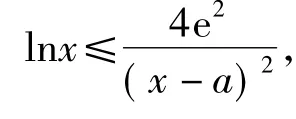
能用为“数”配“形”思想来解的题目一般有2种情况:一种图形是显现的,例如“已知直线y=k(x-3)与圆x2+y2=1有公共点,求实数k的取值范围”,解题时可以直接画出直线和圆的图形;另一种图形是需要通过等价变形来构造的,不同的构造方法可以得到不同的图形,如本文例1.
3 挖掘“数”的几何背景

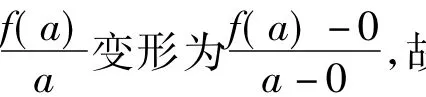
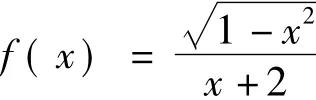
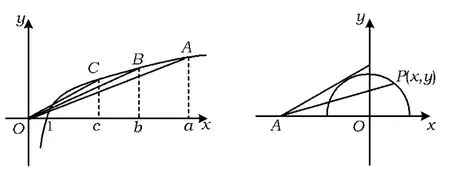
图5 图6
变式1 函数的值域是________.
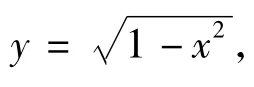
点评例2与变式1的差别在于:例2中的动点P(x,y)所在的曲线是显然的,即在函数f(x)=log2(x+1)的图像上,而变式1中的动点P(x,y)所在的曲线不是一目了然的,需要通过换元、变形,才能将曲线的形状显现出来.
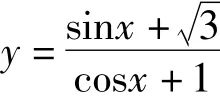
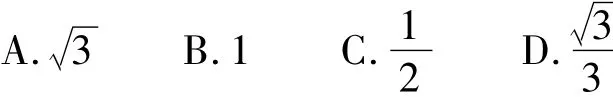
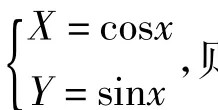
点评变式2经过换元得到单位圆的参数方程.若将sinx或cosx的系数作适当改变,则换元后得到椭圆的参数方程,变式2可以用类似的方法来处理,不过求切线斜率的难度会高一些.
4 转化为曲线的位置关系
例3 不等式x2-2x<logax-1对任意x∈(1,2)恒成立,则 a 的取值范围是 .
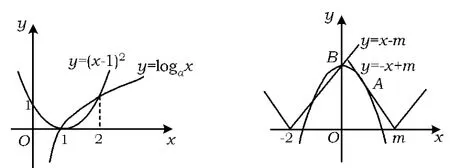
图7 图8
分析将不等式变形为(x-1)2<logax,此不等式左边表示抛物线y=(x-1)2,右边是对数函数y=logax的图像.于是,原命题等价于在区间(1,2)内,对数函数的图像恒在抛物线的上方,如图7所示.因此,只要满足loga2≥1即可,从而1<a≤2.
变式1 函数 f(x)=-x2+2,g(x)=|x-m|,若存在 x0∈(0,+∞)使得 f(x0)≥g(x0)成立,则m的取值范围是 ( )
分析本题是一个存在性问题,函数f(x),g(x)的图像很容易画出.函数g(x)=|x-m|的图像为2条关于x=m对称的射线,其方程分别为y=-x+m和y=x-m(y≥0).

当直线 y=x-m 过点 B(0,2)时,m=-2,这是图像的另一个极端位置.当m≤-2时,不存在x0∈(0,+∞)满足 f(x0)≥g(x0),故 m > -2.
点评不等式问题,从“形”的角度去考虑,等价于不等式2边所对应的图像的位置关系.

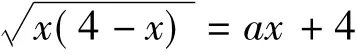

图9 图10
点评方程的根等于2个函数图像的交点的横坐标.因此,讨论根的个数问题从“形”的角度去思考,就等价于讨论2个图像的交点个数问题.
5 利用向量加法的几何意义构图
例4 若非零向量a,b,满足|a+b|=|b|,则( )
A.|2a|> |2a+b| B.|2a|< |2a+b|C.|2b|> |2a+b| D.|2b|< |2a+b|
(2007年浙江省数学高考理科试题)
分析本题用代数方法解非常困难.若能用向量加法运算的三角形法则来构图,则问题可以变得非常直观而简单.
由条件得和向量a+b与向量b的模相等,但夹角不定.由于本题是选择题,可以取特殊角,并结合排除法.让(a+b)⊥b,构造等腰直角△OAB,如图10 所示,其中|OA|=|b|,|AB|=|a|,|OB|=|a+b|.在钝角△OAC中,
|AC|=2|a|,|OC|=|2a+b|.
显然钝角∠AOC所对的边AC最长,故有|2a|>|2a+b|.排除选项 B,C,D,故选 A.
例5 已知平面向量 α,β(α≠0,α≠β)满足|β|=1,且α与β -α的夹角为120°,则|α|的取值范围是_______.
分析由条件知β是单位向量,故其终点可以在单位圆上.又 α与 β-α的夹角为120°(定值),根据向量运算的三角形法可以构造△OAB,让AB=β-α,如图11所示.
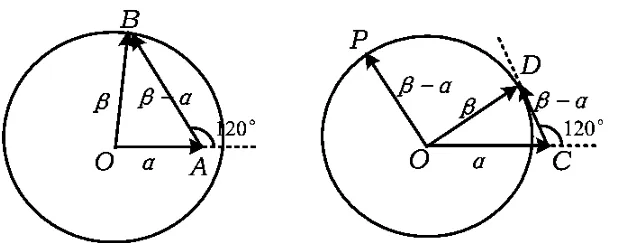
图11 图12
点评向量加法运算的几何意义可用平行四边形法则和三角形法则来刻画,向量的模问题常与圆建立联系,这些都是向量问题构造图形的依据.
为“数”配“形”是一种重要的数学思想,它常与等价转换、分类讨论、函数与方程等数学思想有机地结合在一起.在为“数”配“形”时,还经常会用到换元法、构造法和极端原理等重要的数学方法.因此,笔者认为:有意识地对学生进行为“数”配“形”思想的教学和训练,有利于培养学生创造性意识和创新能力.

