利用过程性变式 创设探究性课堂

●童桂恒 (金华四中教育集团婺城中学 浙江金华 321025)

所谓“过程性变式”是指数学活动的有层次推进.这种层次性既可以表现为一系列的台阶，也可以表现为某种活动策略或经验.在数学活动过程中，教师通过对数学学习对象动态的、内在的、有层次性的递进，让学生分步解决问题，并在解决问题的过程中积累多种活动经验.

1 利用过程性变式，改进定理教学模式

在数学教学中，学生要学习大量的性质定理、判定定理和公式等，以往的数学学习常常是教师“告诉”定理公式，给出证明，然后通过练习做机械训练.学生对这样的教学模式感到枯燥乏味，学习兴趣陡降.因此，在定理教学中利用过程性变式，创设探究性的学习环境，让学生在数学活动中增添数学学习的兴趣，在变式训练中提高数学学习水平.

1.1 用情境问题引发兴趣

案例1 “等腰三角形的判定”课堂教学设计

例1 如图1，如何复原一个被墨迹浸渍的只剩一个底角和一条底边的等腰三角形?

学生的3种方法分别是：

方法1：量出∠C度数，画出∠B=∠C，∠B与∠C的边相交得到顶点A.

方法2：作BC边上的中垂线，与∠C的一边相交得到顶点A.

方法3：对折.

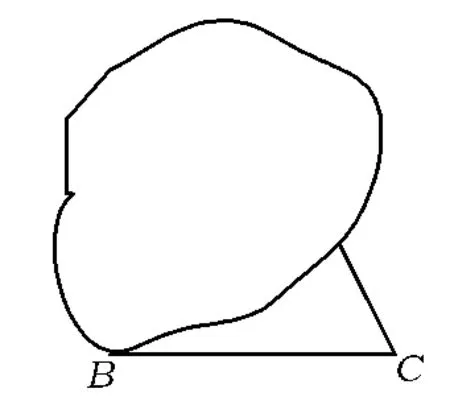
图1

评注“数学知识需要形式化的表述，而教师的责任是返璞归真，运用适度的非形式化方法，将数学的学术形态转化为教育形态，展现数学的魅力，激起学生学习数学的热情”.几何源于现实生活，对于初学平面几何的学生来说，选择适当的时机，让他们从个体实践检验中学习，可以提高学习的主动性.在这里，第1种方法正好可以得出本节课要学的判定定理，第2种方法则是今后线段垂直平分线性质的事实基础，第3种方法则是等腰三角形对称性的体现.在探究的活动过程中，等腰三角形的判定定理不是由教师给出，而是让学生凭借经验画图，那么画出的图形是不是等腰三角形呢?产生了问题，然后从问题出发，得出判定定理.这样做，改变了学生被动接受的状况，从而提高了学生的学习兴趣和学习热情.

1.2 多种证法激活创造力

例1的3种常规的证法如下：

(1)如图2，作∠A的平分线，利用“角角边”证明;

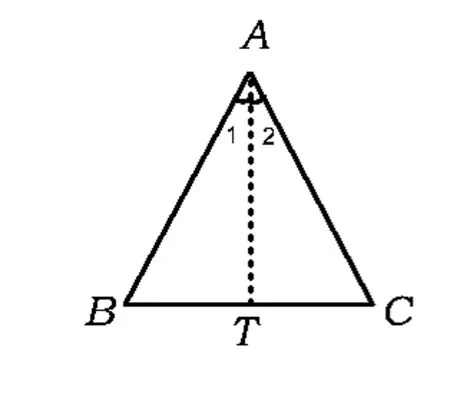
图2

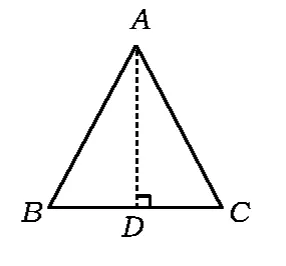
图3

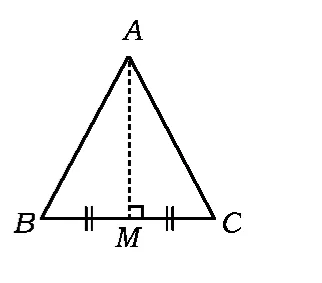
图4

(2)如图3，过点A作边BC的垂线，利用“角角边”证明;

(3)如图4，作边BC上的中线，“边边角”，不能证明.

例1的2种创造性的证法如下：

(1)如图5，假定AB＞AC，由“大边对大角”得出矛盾;

(2)如图6，△ABC≌△ACB，应用“角边角”进行证明.

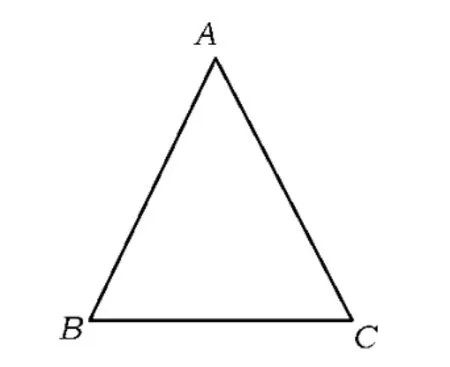
图6

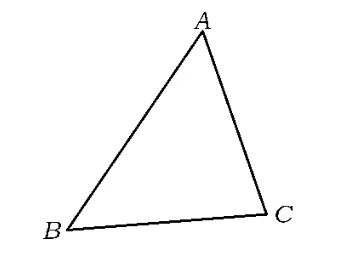
图5

评注由于这节课利用学生的画图经验导出等腰三角形的判定定理，学生感到亲切、自然，论证兴趣很浓.第2种常规证法虽然是错误的，但学生在证明的过程中能发现问题，这种错误的尝试可使学生吸取教训，积累经验，增长解题的能力，以后解决问题时可以少走“弯路”，避免盲目尝试.2种不添辅助线的创造性证法，说明学习兴趣的力量是不可低估的，学生学习的潜能是无限的.

1.3 用变式练习分步解决问题

通过不断变换题目的条件，使不同数学学习水平的学生在数学活动中得到不同的发展.

(1)如图 7所示，在△ABC中，∠ABC=∠ACB，BO平分∠B，CO平分∠C.能得出什么结论?

(2)若过点O作直线EF∥BC.图8中有几个等腰三角形?为什么?线段EF与线段BE，FC之间有何关系(学生编题)?

(3)若∠B与∠C不相等.图9中有没有等腰三角形?为什么?线段EF与线段BE，FC之间还有没有关系(学生讨论)?

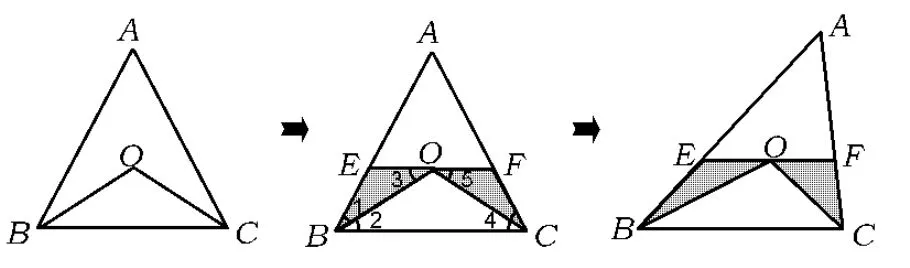
图7图8图9

评注数学知识本身是一个多层次的结构系统.上述变式练习实际上经历了3步：在图7中，学生直观看到一个等腰三角形，只需简单应用判定定理(直观水平);在图8中，直观看到有3个等腰三角形，但2个阴影三角形必须应用判定定理进行推理论证(简单推理水平);在图9中，必须综合应用判定定理和性质定理，才能得出线段间的关系(综合应用定理水平).通过有层次的推进，使学生分步解决问题，积累了数学论证的活动经验和策略.

人的认识往往是从特殊到一般然后又到特殊的过程，课堂教学的有层次递进正是基于数学知识的结构和人的认识的这一规律，加上学生在学习准备上的差异性，教学的层次性使得不同学习水平的学生在教学进程的各个阶段各有所获，这是一种适合学生的教育.

2 利用过程性变式，彰显概念建构过程

数学概念是对数学研究对象的高度抽象和概括，是导出数学定理法则的逻辑基础，是构建数学理论大厦的基石.在概念教学中，教师要精心创设情景，让学生像数学家那样去“想数学”，使数学概念的形成过程成为发现、创新的过程.

案例2 “同类项”概念形成过程的教学

在同类项概念学习过程中，掌握同类项概念的本质属性和非本质属性是教学的重点，引导学生体验同类项概念的形成过程是教学的难点.为此，笔者设计了以下6个环节.

赛一赛 求代数式-7x2+12x+6x2-9x+x2-2x-1的值.

(请一位学生说出一个关于x的1位(或2位)整数，教师和另一位学生比赛，看谁先求出正确答案.)

找一找 以下几组代数式有什么相同点?

(1)2x和 -3x;(2)5st和7ts;(3)-0.5x3y2和y2x3;(4)ab2c和 -ab2c.

(2人一小组合作学习，教师引导质疑，总结这几组代数式的相同点，引出同类项的概念.)

评注在概念引入时，教师要根据概念类型，为学生创设生动形象的教学情境.根据七年级学生的心理规律，通过“赛一赛”这个师生竞赛的方式，能激发起学生的求知欲望，增强学生自主学习的内驱力.通过“找一找”的活动过程，达到展示知识形成过程，促进学生概念形成的目的.

想一想 5a2b与ba2是同类项吗?为什么?(得出同类项的特点——2个“无关”：与字母顺序无关;与系数无关.)

(得出同类项的特点——2个“相同”：所含字母相同;相同字母的指数也相同.另外，所有常数项也看做同类项.)

评注在概念形成之后，教师要引导学生对概念作进一步的探讨，通过辨析变式和等价深化变式，使学生对概念有更加深刻的理解，让学生既知其然，又知其所以然.

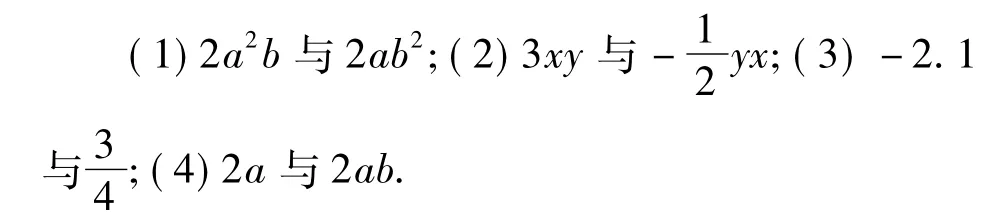
游戏过程：(1)把20张卡片分发给学生;(2)教师随意叫一位学生，这位学生高举自己的卡片;(3)其他学生观察自己手中的卡片和这位学生卡片上的单项式，若认为它们是同类项的，也请站起来;(4)每个学生都是裁判，看看有没有找错朋友.

评注巩固是概念教学的重要环节.心理学原理告诉我们，概念一旦获得，如不及时巩固，就会被遗忘.因此，在教学中要根据学习目标和学习交流中所反馈的信息，精心选编题目，并选择适合学生现状的学习活动方式，让学生在解答、变式、探索中，深化对概念的理解，促进认知结构的内化过程，培养学生创造性的思维品质.

3 利用过程性变式，提升例题教学价值

例题教学是数学课堂教学的重要环节之一，通过例题，学生对所学的概念、定理、公式、法则、方法和思想等，可以获得更进一步的认识.同时，又可启迪学生思维，示范学生解题，培养学生能力.因此，在例题教学中，若能启发学生多角度、多层次、全方位地思考，并对例题进行变式、探索、推广和引申，充分挖掘例题的潜在功能，则必能更有效地开发学生智力，培养创新意识，提高解题水平，充分发挥例题的教学价值.

案例3 一道经典习题的变式教学

玩一玩 游戏名称：“找同类项朋友”.

游戏目的：培养学生主动参与、积极合作、勇于探究的精神，并巩固同类项概念.

游戏材料：20张卡片，卡片上写着单项式，如

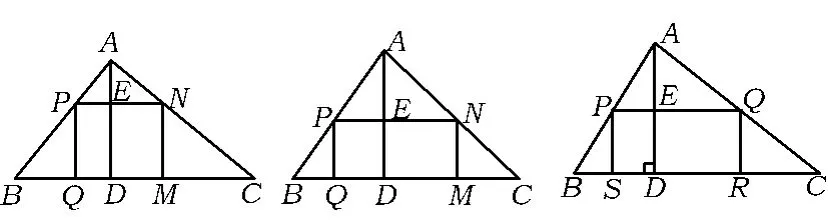
图10 图11 图12

例2 如图10，有一块三角形余料ABC，它的边BC为12 cm，高AD为8 cm.要把它加工成正方形零件，使正方形的一边在BC上，其余2个顶点分别在AB，AC上.问正方形零件的边长是多少?

变式1 如图11，将例2中“正方形PQMN”改为“矩形PQMN”，其他条件不变.矩形的长和宽分别为多少时，所截得的矩形面积最大?最大面积是多少?

变式2 如图11，一块铁皮呈现锐角三角形，它的边BC为12 cm，高AD为8 cm，要求加工成的矩形一边在BC上，另外2个顶点在AB，AC上.

(1)试问：这个三角形能否加工成一个面积为24 cm2的矩形零件?能否加工成一个面积为32 cm2的矩形零件?理由是什么?

(2)从第(1)小题的结论中，试猜想这个三角形内接的矩形面积与原三角形面积有何关系?不需要说明理由.

若从内接矩形和原三角形面积之间的关系考虑，不妨设△APQ的面积与矩形PQRS面积相等，于是有：

变式3 如图11，在△ABC中，点P，N分别在AB，AC上，点 Q，M 在 BC上，四边形 PQMN是矩形，若矩形PQMN的面积与△APN的面积相等，求PN ∶BC的值.

若将变式3所求的结论与已知条件调换，则有：

变式4 如图11，在△ABC中，点P，N分别在AB，AC上，点 Q，M 在 BC上，四边形 PQMN是矩形，若 PN ∶BC=2 ∶3，求矩形 PQMN面积与△APN的面积比值.

由于例2中△ABC的形状不确定，不妨把△ABC设为直角三角形，令∠BAC=90°，有：

变式5 如图 12，一块铁皮呈三角形，∠BAC=90°，要把它加工成矩形零件，使矩形一边位于BC上，另外2个顶点分别在边AB，AC上.试问：PS，BS，CR之间有何关系?为什么?

变式6 一块直角三角形木板的一条直角边AB 长为1.5 m，面积为1.5 m2，工人师傅要把它加工成一个面积最大的正方形桌面，请甲、乙2位同学设计加工方案，甲设计方案如图13所示，乙设计方案如图14所示.你认为哪位同学设计的方案较好?试说明理由(加工损耗忽略不计，计算结果可保留分数).

图13 图14 图15

变式7 已知△ABC是直角三角形，∠ACB=90°，AC=80，BC=60，如图 15 所示，把边长分别为x1，x2，x3，…，xn的 n 个正方形依次放入△ABC 中，则第1个正方形的边长x1= ______;第n个正方形的边长xn= ______(用含n的式子表示，n≥1).

变式8 在Rt△ABC中，∠ACB=90°，AC=4，BC=3.

(1)如图16，四边形DEFG为Rt△ABC的内接正方形，求正方形的边长;

(2)如图17，三角形内有并排的2个相等的正方形，它们组成的矩形内接于Rt△ABC，求正方形的边长;

(3)如图18，三角形内有并排的3个相等的正方形，它们组成的矩形内接于Rt△ABC，求正方形的边长;

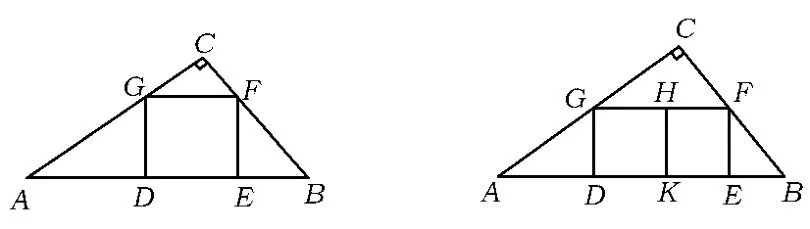
图16 图17

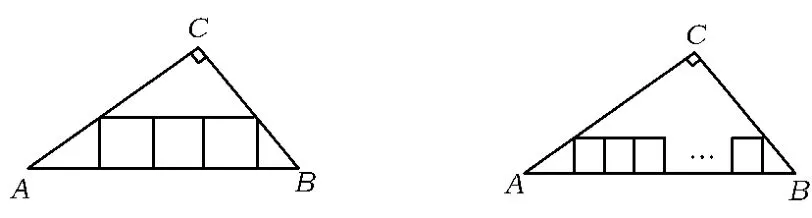
图18 图19

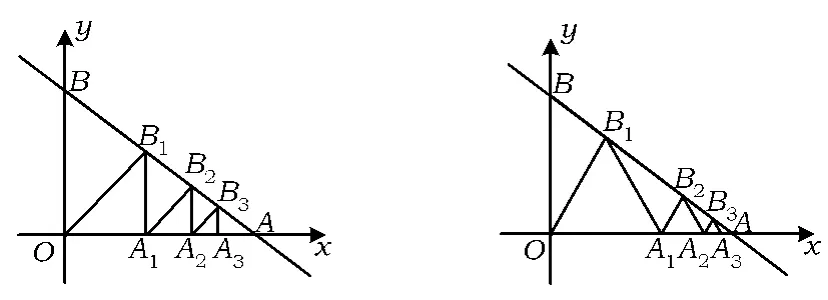
图20 图21

(4)如图19，三角形内有并排的n个相等的正方形，它们组成的矩形内接于Rt△ABC，求正方形的边长.变式9 如图20，在直线y=-x+60与x轴、y轴所围成的△AOB中，依次放入腰长分别为x1，x2，x3，…，xn的 n 个等腰直角三角形，则 x1=_______，xn= ______(或求 A1，A2，A3，…，An的横坐标).

若把条件“等腰直角三角形”改变为“等边三角形”，则有：

变式10 如图21，在直线y=-x+60与x

轴、y轴所围成的△AOB中，依次放入边长分别为x1，x2，x3，…，xn的 n 个等边三角形，试猜想第 n 个等边三角形的边长.

进一步，把“直线”这个条件改变为“双曲线”或者“抛物线”，就有下面的变式：

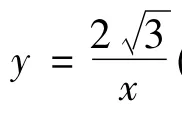
nnn△P1OA1，△P2A1A2，△P3A2A3，…，△PnAn-1An都是等边三角形，边 OA1，A1A2，A2A3，…，An-1An都在 x轴上.

(1)求点P1的坐标;

(2)求y1+y2+y3+…+yn的和.

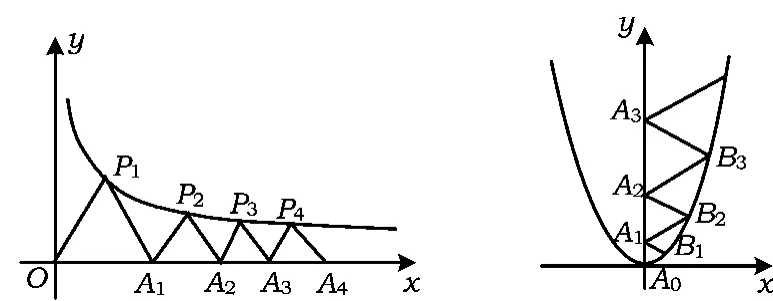
图22 图23

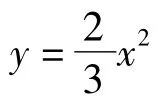
［1］ 周成平.中国著名教师的精彩课堂(初中数学卷)［M］.南京：江苏人民出版社，2009.

［2］ 顾泠沅，杨玉东.过程性变式与数学课例研究［J］.上海中学数学，2007(1/2)：1-5.