从圆到椭圆——一类高考试题的设计方法

●

(建湖县高级中学 江苏建湖 224700)

从圆到椭圆
——一类高考试题的设计方法

●卜以军

(建湖县高级中学 江苏建湖 224700)

1 重庆卷(理)第20题的设计方法

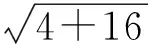
从而点P1的轨迹是圆C1：x2+y2=20.

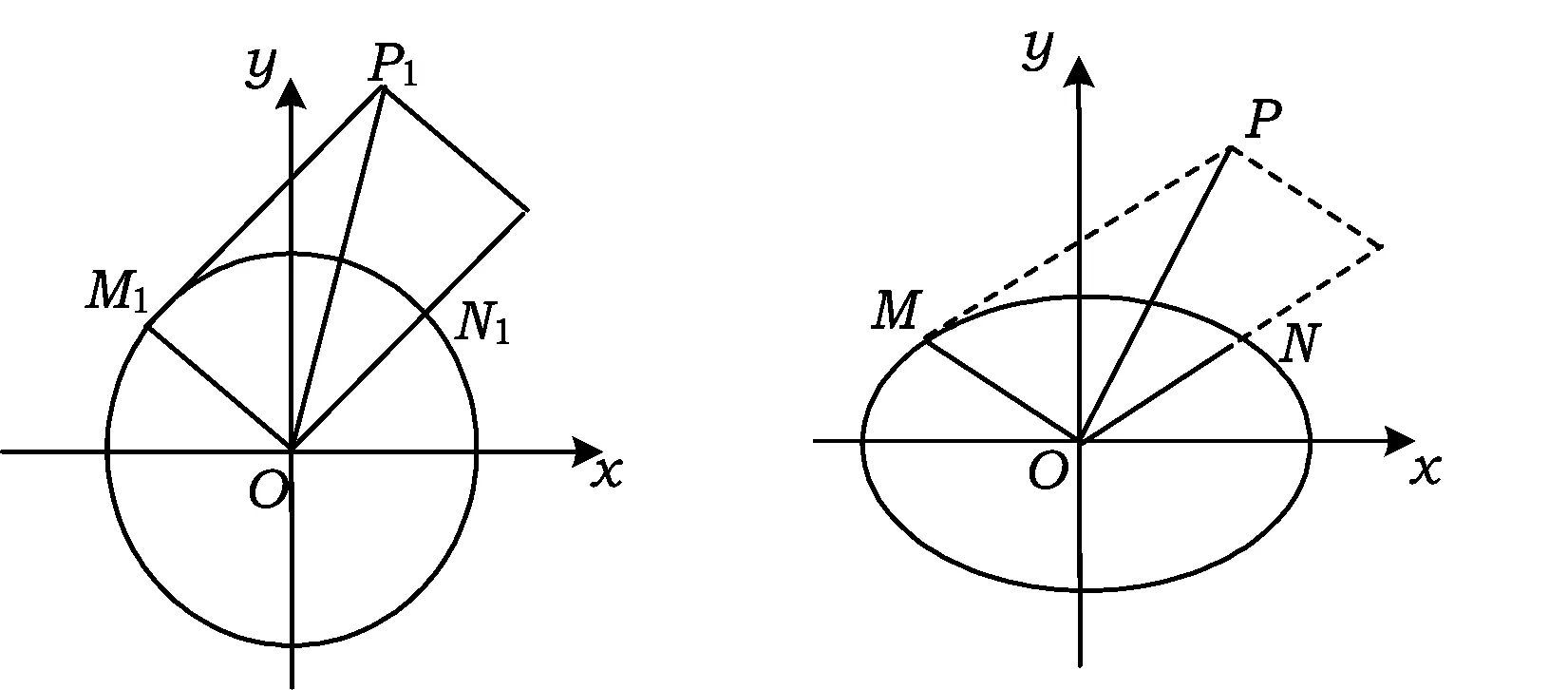
图1 图2

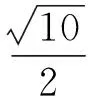
(1)求该椭圆的标准方程.

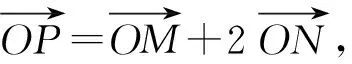
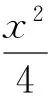
2 江苏卷第18题的设计方法

如图3，若P1A1是圆O:x2+y2=4的直径，且不在坐标轴上，过点P1作x轴的垂线，垂足为C1，联结A1C1，并延长交圆于点B1，则直线P1A1的斜率与直线P1B1的斜率有什么关系？

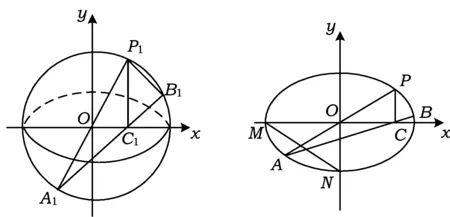
图3 图4

设点P1的坐标为(x1,y1)，则A1(-x1,-y1),C1(x1,0),从而

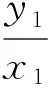
即

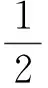
因为P1A1是圆O的直径， 所以P1B1⊥A1C1，从而

kP1B1·kA1C1=-1,

即

kP1B1·kP1A1=-2.

因此，对于上述的圆和直线，只要直线P1A1和P1B1的斜率都存在，就总有P1A1和P1B1的斜率之积为定值-2.

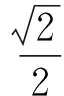
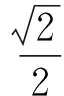
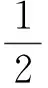
从而PA⊥PB.这就形成了江苏卷第18题：

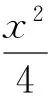
(1)当直线PA平分线段MN时，求k的值；

(2)当k=2时，求点P到直线AB的距离d；

(3)对任意k>0，求证：PA⊥PB.

3 山东卷(理)第22题的设计方法

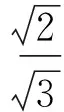
又设P(x1,y1)，Q(x2,y2)，则

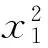
3(cos2α+sin2α)=3,

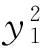
2(sin2α+cos2α)=2.

图5 图6

这就是山东卷(理)第22题的第(1)小题，也是该题的基础和关键.原试题如下：

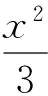
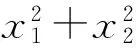
(2)设线段PQ的中点为M，求|OM|·|PQ|的最大值.

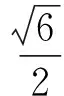
4 四川卷(理)第21题的设计方法

圆的这个性质不容易发现，证明过程也比较复杂.证明过程如下：

设直线l的方程为

y=kx+m(k≠0,m≠0,±ka+m≠0),

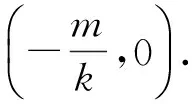
(1+k2)x2+2kx+m2-a2=0,

从而

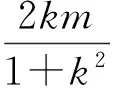
直线AC的方程为

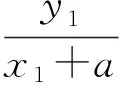
直线BD的方程为

联立2个方程得

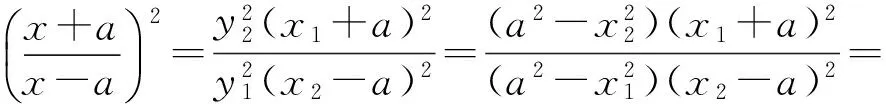
y1y2=k2x1x2+km(x1+x2)+m2=

所以

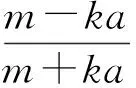
从而

即

解得

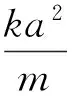
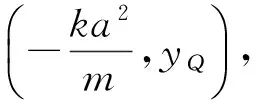
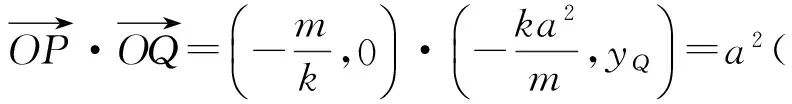
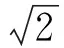
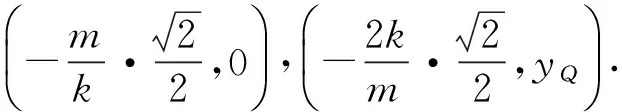
图7

例4如图7，椭圆有2个顶点A(-1，0)，B(1，0)，过其焦点F(0，1)的直线l与椭圆交于点C，D，并与x轴交于点P，直线AC与直线BD交于点Q．

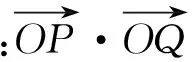
从以上的分析中可知，椭圆中的定点、定值、垂直等问题，可以先在圆上进行研究，得到一个正确的结论后，再通过变换得到椭圆上的与之相对应的结论.或将圆的一些熟知的结论类比到椭圆上，再进行深入的研究，得到椭圆的一个正确的结论，然后进行加工、改编，形成一道适合中学生进行知识巩固、方法训练、能力测试、选拔考试的试题.这是一种常用的非常有效的命题方法.